3 Cara Mudah Menyelesaikan Persamaan Kuadrat | Matematika Kelas 9

Gimana sih, cara menyelesaikan persamaan kuadrat dalam matematika? Yuk, simak tiga cara mudah beserta contohnya berikut ini!
—
Dalam mempelajari ilmu matematika, kamu bakalan banyak bertemu, berkenalan, bahkan berteman sama yang namanya persamaan.
Jenis-jenis persamaan dalam matematika pun ada banyak, lho! Ada persamaan linier, persamaan kuadrat, persamaan eksponen, persamaan logaritma, persamaan trigonometri, dan lain sebagainya. Duh, denger namanya aja, udah bikin pusing duluan, ya?
Eits, tenang, guys! Belajar matematika itu nggak pusing kok, asalkan kita bisa memahami konsepnya terlebih dahulu sebelum lanjut mempelajari lebih jauh dan mengerjakan latihan soal.
Nah, kali ini, kita akan belajar bersama tentang persamaan kuadrat, nih! Biar kamu paham konsepnya, kita mulai dari pengertian persamaan kuadrat dulu, ya.
Apa itu Persamaan Kuadrat?
Persamaan kuadrat adalah persamaan polinomial (suku banyak) variabel 1 yang memiliki pangkat tertinggi dua. Ingat, ya, pangkat tertingginya dua! Jadi, kalau kamu nyariin pangkat tiga di persamaan kuadrat, ya kagak bakalan ketemu, yak.
Nah, bentuk umum persamaan kuadrat bisa dituliskan seperti berikut:
ax2 + bx + c = 0
Dengan a, b, c ∈ R dan a ≠ 0
Keterangan:
x = variabel
a = koefisien dari x2
b = koefisien dari x
c = konstanta
Dalam mempelajari persamaan kuadrat, tentunya kamu nggak akan terlepas dari yang namanya menyelesaikan persamaan kuadrat. Hmm, menyelesaikan tuh, maksudnya gimana sih? Emangnya persamaan kuadrat punya masalah, kok harus diselesaiin segala?
Tentu punya, dong! Masalah yang dimiliki persamaan kuadrat terletak pada nilai x-nya.
Jadi, seperti yang udah kita tau dari bentuk umumnya, persamaan kuadrat itu punya variabel x yang nggak diketahui nilainya berapa. Nah, nilai x inilah yang mau kita cari! Cara mencari nilai x adalah dengan menyelesaikan persamaan kuadrat tersebut.
Terus, cara menyelesaikan persamaan kuadrat kaya gimana, kak?
Cara Menyelesaikan Persamaan Kuadrat
Ada tiga cara untuk menyelesaikan persamaan kuadrat, yaitu dengan menggunakan faktorisasi, kuadrat sempurna, dan rumus kuadratik atau biasa disebut juga sebagai rumus ABC. Kita bahas satu per satu, ya!
Baca Juga: Cara Menyusun Persamaan Kuadrat dan Contohnya
1. Faktorisasi
Faktorisasi atau pemfaktoran merupakan cara mencari penyelesaian dari persamaan kuadrat, dengan cara mencari nilai yang jika dikalikan, maka akan menghasilkan nilai lain.
Ada tiga bentuk persamaan kuadrat dengan faktorisasi yang berbeda, yakni seperti berikut:
| No. | Persamaan Kuadrat | Faktorisasi |
| 1. | x2 + 2xy + y2 = 0 | (x + y)2 = 0 |
| 2. | x2 − 2xy + y2 = 0 | (x − y)2 = 0 |
| 3. | x2 − y2 = 0 | (x + y)(x − y) = 0 |
Dengan x = variabel dan y = konstanta
Next, coba kita kerjakan contoh soal di bawah ini, ya!
Contoh Soal Faktorisasi
Selesaikan persamaan kuadrat berikut dengan cara faktorisasi 5x2 + 13x + 6 = 0!
Jawab:
5x2 + 13x + 6 = 0
5x2 + 10x + 3x + 6 = 0
5x(x + 2) + 3(x + 2) = 0
(5x + 3)(x + 2) = 0
5x = −3
x = ![]() atau x = −2
atau x = −2
Jadi, penyelesaiannya adalah x = ![]() atau x = −2.
atau x = −2.
Lanjuuut, ke pembahasan cara kedua, yaitu kuadrat sempurna.
2. Kuadrat Sempurna
Kuadrat sempurna adalah cara untuk menyelesaikan persamaan kuadrat dengan melengkapkan kuadratnya sehingga menjadi sempurna. Bentuk persamaan kuadrat sempurna merupakan bentuk persamaan yang menghasilkan bilangan rasional.
Penyelesaian persamaan kuadrat dengan kuadrat sempurna menggunakan rumus berikut:
(x + p)2 = x2+ 2px + p2
Dari bentuk tersebut, kamu bisa ubah menjadi bentuk persamaan dalam (x + p)2 = q
Penyelesaian:
(x + p)2 = q
x + p = ± √q
x = −p ± √q
Biar makin paham, coba kerjakan contoh soal di bawah ini, ya!
Contoh Soal Kuadrat Sempurna
Lengkapi bentuk kuadrat sempurna berikut ini x2 + 6x + 5 = 0!
Jawab:
x2 + 6x + 5 = 0
Ubah menjadi x2 + 6x = −5
Tambahkan satu angka di ruas kiri dan kanan agar menjadi kuadrat sempurna. Penambahan angka ini diambil dari separuh angka koefisien dari x atau separuhnya 6 yang dikuadratkan, yakni 32 = 9. Tambahkan angka 9 di ruas kiri dan kanan, sehingga persamaannya menjadi:
x2 + 6x + 9 = −5 + 9
x2 + 6x + 9 = 4
(x + 3)2 = 4
(x + 3) = √4
x + 3 = ± 2
a. Untuk x + 3 = 2
x = 2 − 3
x = −1
b. Untuk x + 3 = −2
x = −2 − 3
x = −5
Jadi, penyelesaiannya adalah x = −1 atau x = −5.
Baca Juga: Ketahui Sifat-Sifat Bentuk Akar & Cara Merasionalkannya
Lanjuuut, ke cara terakhir, yakni rumus kuadratik!
3. Rumus Kuadratik
Selain menggunakan faktorisasi dan melengkapi kuadrat sempurna, persamaan kuadrat juga bisa diselesaikan dengan menggunakan rumus kuadratik atau biasa dikenal dengan rumus ABC. Rumus kuadratik atau rumus ABC bisa kamu lihat pada gambar berikut.

Next, coba kamu kerjakan contoh soal berikut!
Contoh Soal Rumus Kuadratik
Selesaikan persamaan kuadrat x2 + 4x − 12 = 0 menggunakan rumus kuadratik (rumus ABC)!
Jawab:
x2 + 4x − 12 = 0
a = 1, b = 4, c = −12
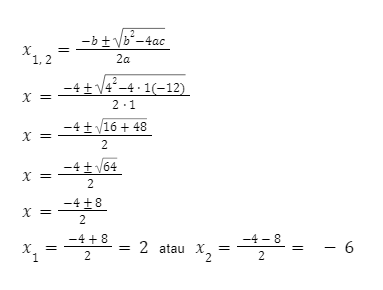
Jadi, penyelesaiannya adalah x = 2 atau x = −6.
—
Nah, itu dia pembahasan tentang cara menyelesaikan persamaan kuadrat. Sudah paham, kan? Kalau kamu masih bingung dan masih ada pertanyaan terkait materi ini, langsung saja tanyakan melalui Roboguru!
Referensi:
Wagiyo, A., Mulyono, S., dan Susanto. (2008). Pegangan Belajar Matematika. Jakarta: Kemendikbud.
















