Eksponen (Bilangan Berpangkat): Pengertian, Sifat & Contoh | Matematika Kelas 9

Apa yang dimaksud dengan eksponen? Di artikel Matematika kelas 9 kali ini, kita akan membahas materi eksponen atau bilangan berpangkat, mulai dari pengertian, sifat-sifat, hingga contoh soalnya. Yuk, simak!

—

Salah satu permasalahan yang dihadapi oleh Indonesia adalah jumlah populasi penduduk yang sangat banyak. Menurut data Worldometer, jumlah populasi penduduk di Indonesia saat ini (Juni 2022) adalah sekitar 279.218.329 penduduk.

Jumlah ini setara dengan 3,51% dari total populasi penduduk di dunia. Dengan jumlah ini, Indonesia menempati peringkat ke-4 negara dengan jumlah penduduk tertinggi di dunia setelah Tiongkok, India, dan United States.

Nah, tahu nggak sih, dalam ilmu matematika, untuk menghitung data yang sangat banyak, seperti data jumlah populasi penduduk, data angka kelahiran dan angka kematian di dunia, serta data-data lain yang angkanya mencapai ratusan juta, kita bisa menggunakan yang namanya eksponen. Apa itu eksponen?

Pengertian Eksponen (Bilangan Berpangkat)

Eksponen adalah bilangan berpangkat, yakni bilangan yang dikalikan dengan dirinya sendiri hingga beberapa tingkat. Notasi pangkat digunakan untuk menuliskan berapa kali suatu bilangan dikalikan secara berulang dalam bentuk yang lebih sederhana.

Misalnya, kita memiliki faktor a yang dikalikan berulang sebanyak tiga kali, maka dapat ditulis:

a³ = a x a x a

Angka 3 dituliskan di sebelah kanan atas a, yang menunjukkan bahwa angka 3 ini merupakan pangkat dari a.

Contohnya, 2³ = 2 x 2 x 2 = 8

Baca Juga: Cara Menyusun Persamaan Kuadrat dan Contohnya

Supaya kamu lebih paham, perhatikan gambar di bawah ini!

Bilangan berpangkat bisa terdiri atas bilangan dengan pangkat bulat positif (bilangan asli), bilangan dengan pangkat bulat negatif, bilangan dengan pangkat nol, bilangan dengan pangkat rasional, dan bilangan dengan pangkat riil.

Sifat-Sifat Eksponen (Bilangan Berpangkat)

Bilangan berpangkat atau eksponen memiliki sifat-sifat yang perlu kamu pahami agar kamu bisa menyelesaikan persamaan eksponen maupun pertidaksamaan eksponen dengan lebih mudah. Ada 8 sifat eksponen yang sudah dirangkum dalam gambar berikut. Cus, kita bahas!

1. Pangkat Penjumlahan

Jika ada perkalian eksponen dengan basis yang sama, maka pangkatnya harus ditambah. Bisa dituliskan sebagai berikut:

a^m x aⁿ = a^{m + n}

Contoh: 2⁴ x 2² = 2^{4 + 2} = 2⁶ = 64

2. Pangkat Pengurangan

Jika ada pembagian eksponen dengan basis yang sama, maka pangkatnya harus dikurang. Bisa dituliskan sebagai berikut:

a^m : aⁿ = a^{m – n}

Contoh: 2⁵ : 2³ = 2^{5 – 3} = 2² = 4

3. Pangkat Perkalian

Jika ada bilangan berpangkat yang dipangkatkan lagi, maka pangkatnya harus dikali. Bisa dituliskan sebagai berikut:

(a^m)ⁿ = a^{m x n}

Contoh: (2²)³ = 2^{2 x 3} = 2⁶ = 64

4. Perkalian Bilangan yang Dipangkatkan

Jika ada perkalian bilangan yang dipangkatkan, maka masing-masing bilangan tersebut dipangkatkan juga. Bisa dituliskan sebagai berikut:

(a . b)^m = a^m . b^m

Contoh: (2 x 3)² = 2² x 3² = 4 x 9 = 36

Baca Juga: Mengenal Konsep Transformasi Geometri dan Latihan Soal

5. Perpangkatan pada Bilangan Pecahan

Jika ada bilangan pecahan yang dipangkatkan, maka bilangan pembilang dan penyebutnya harus dipangkatkan semua, dengan syarat b ≠ 0, artinya penyebutnya tidak boleh sama dengan 0. Bisa dituliskan sebagai berikut:

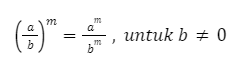
Contoh:

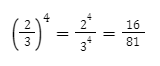
6. Pangkat Negatif

Jika ada bilangan berpangkat negatif, maka nilainya sama dengan 1 per bilangan eksponen tersebut namun pangkatnya menjadi positif. Bisa dituliskan sebagai berikut:

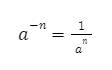
Contoh: 

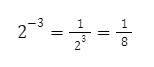
7. Pangkat Pecahan

Jika ada bilangan berpangkat yang diakar, maka pangkat dari akarnya dapat ditulis menjadi penyebut dari pangkat bilangannya. Bisa dituliskan sebagai berikut:

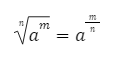
Contoh: 

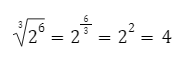
8. Pangkat Nol

Jika ada bilangan yang berpangkat nol, maka hasilnya sama dengan 1 berapapun nilai bilangan basisnya, dengan syarat bilangan basisnya tidak sama dengan 0 (a ≠ 0). Bisa dituliskan sebagai berikut:

a⁰ = 1, untuk a ≠ 0

Contoh: 

• 2⁰ = 1
• 7⁰ = 1

—

Kamu sudah tahu belum, kalau materi ini juga bisa dipelajari di ruangbelajar dengan fitur Adapto, lho! Yuk, cobain fiturnya sekarang!

Bilangan Negatif Berpangkat

Selain 8 sifat eksponen yang sudah kita bahas di atas, kamu juga perlu tahu sifat dari bilangan berpangkat jika bilangan basisnya bernilai negatif. Perhatikan gambar di bawah ini!

a. Bilangan Negatif Berpangkat Ganjil

Suatu bilangan negatif, jika dipangkatkan dengan bilangan ganjil, maka hasilnya adalah bilangan negatif. Dapat dituliskan sebagai berikut:

(-a)^m = -a^m , dengan m = ganjil

Contoh: 

(-2)³ = -(2³)

(-2) x(-2) x(-2) = -(2 x 2 x 2)

-8 = -8

b. Bilangan Negatif Berpangkat Genap

Suatu bilangan negatif, jika dipangkatkan dengan bilangan genap, maka hasilnya adalah bilangan positif. Dapat dituliskan sebagai berikut:

(-a)ⁿ = aⁿ , dengan n = genap

Contoh:

(-2)² = 2²

(-2) x(-2) = 2 x 2

4 = 4

Baca Juga: Bentuk Akar, Sifat-Sifat dan Cara Merasionalkannya

Sudah paham sifat-sifat bilangan berpangkat (eksponen)? Sekarang, saatnya kita terapkan sifat-sifat perpangkatan ini dalam mengerjakan latihan soal! Yuk, kerjakan contoh soal berikut ini!

Contoh Soal Eksponen

1. Hasil dari 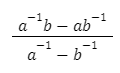 adalah …

Penyelesaian:

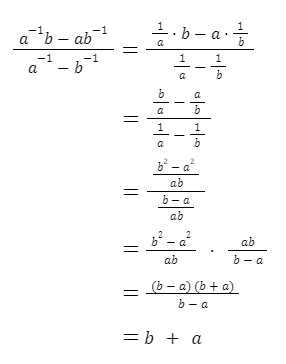
Jadi hasil dari 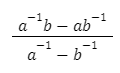adalah b + a.

—

Itulah penjelasan tentang eksponen atau bilangan berpangkat, mulai dari pengertian, sifat-sifat, hingga contoh soalnya. Gimana? Gampang, kan? Yuk, semangat terus belajarnya! Kalau kamu butuh guru privat matematika, langsung aja yuk, gabung dengan Ruangguru Privat Matematika!

Referensi:

Subchan, Winarni, Hanafi L, dkk. (2015). Matematika SMP/MTs Kelas IX Semester 1. Jakarta: Kementerian Pendidikan dan Kebudayaan.