Macam-Macam Transformasi Geometri, Sifat & Contoh Soal | Matematika Kelas 9

Yuk, kita belajar bersama mengenai konsep transformasi geometri, jenis-jenis, sifat, hingga contoh soalnya supaya kamu semakin paham! Simak sampai habis artikel Matematika kelas 9 ini, ya.
—
Apa yang terlintas dipikiran kamu kalo denger kata transformasi?
Wah pasti bervariasi banget deh!
Ada yang langsung kepikiran film transformers atau mungkin lagi mikirin transformasi ulat menjadi kupu-kupu.
Secara nggak sadar, kedua hal tadi berhubungan loh sama materi yang kita bahas kali ini. Contohnya, ulat yang berubah menjadi kepompong lalu berubah lagi menjadi kupu-kupu. Terus, kalo transformer sama juga sih. Jadi, sebuah mobil yang berubah menjadi robot berukuran besar.
Nah, dari kedua hal itu kita bisa tau deh arti dari transformasi, yaitu perubahan (bisa perubahan posisi atau ukuran ya). Terus, arti geometri apa dong? Geometri itu sesuatu yang berhubungan sama titik, garis atau bidang.
Jadi, bisa disimpulkan nih bahwa transformasi geometri adalah suatu perubahan posisi atau ukuran pada titik, garis atau bidang. Misalnya, posisi awal (x,y) ketika mengalami transformasi posisinya menjadi (x’,y’).
Jenis-jenis Transformasi Geometri ada 4, yaitu:
- Translasi atau pergeseran
- Refleksi atau pencerminan
- Rotasi atau perputaran
- Dilatasi
Supaya kamu nggak ngah-ngoh-ngah-ngoh, kita bahas satu per satu, yuk!
Baca Juga: Eksponen (Bilangan Berpangkat): Pengertian, Sifat & Contoh
1. Translasi (Pergeseran)
Translasi adalah perpindahan (pergeseran) suatu objek. Jika dinyatakan dalam koordinat Cartesius, translasi merupakan perpindahan titi-titik koordinat dari suatu objek ke arah dan jarak tertentu. Nah, translasi ini, hanya arah dan jaraknya aja yang berubah ya, sedangkan ukuran objeknya masih sama.
Translasi biasanya disimbolkan dengan T. Biasanya, suatu soal akan menanyakan titik bayangan dari hasil translasi. Rumusnya cukup mudah, kok. Kamu bisa lihat pada infografik di bawah ini:
Rumus Umum Translasi

Beneran gampang kan? kamu tinggal menjumlahkan koordinat titik awal dengan translasinya. Setelah itu kamu dapetin titik koordinat bayangan A’(x’,y’). Oke, supaya kamu lebih paham, simak contoh soal di bawah ini, yuk!
Contoh Soal Translasi
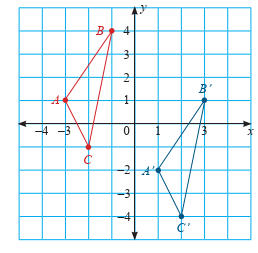
Segitiga ABC mengalami translasi atau pergeseran hingga berada di posisi A’B’C’. Kita akan mencari tahu, berapa sih jumlah pergeseran segitiga ABC tersebut?
Pembahasan:
Untuk menentukan jumlah translasi segitiga ABC, kita bisa hitung jarak satuan antara segitiga ABC dengan A’B’C’ ke arah sumbu-x dan sumbu-y.
Misalnya, kita ambil satu titik untuk kita amati, yaitu titik A. Koordinat A = (-3,1), sedangkan koordinat A’ = (1,-2). Berdasarkan rumus translasi, kita bisa mencari jumlah pergeserannya dengan cara:
A(x,y) (a/b) —> A'(x’,y’)
(-3,1) (a/b) —> (1,-2)
(-3,1) (a/b) —> (-3 + a = 1, 1 + b = -2)
-3 + a = 1
a = 1 + 3
a = 4
1 + b = -2
b = -2 – 1
b = -3
Sehingga, didapat faktor translasinya adalah (a/b) = (4/-3). Artinya, segitiga ABC bergeser 4 satuan ke arah sumbu-x positif (a = 4) dan 3 satuan ke arah sumbu-y negatif (b = -3).
Baca Juga: Perbedaan Kesebangunan dan Kongruen pada Bangun Datar
2. Refleksi (Pencerminan)
Siapa sih yang nggak pernah bercermin?
Aku mah rajin banget bercermin hehehehe.
Refleksi adalah perpindahan titik koordinat suatu objek ke arah dan jarak tertentu, namun perpindahannya bersifat seperti cermin. Kebayang nggak?
Intinya, konsep dari refleksi atau pencerminan ini sama aja dengan sifat di cermin datar.
Sifat-Sifat Refleksi
- Sumbu-x atau sumbu-y dianalogikan sebagai cermin atau pusat refleksi antara bayangan dan benda asli,
- Jarak titik asal objek dengan cermin = jarak titik akhir (bayangan) objek dengan cermin,
- Garis yang menghubungkan titik objek dengan bayangannya, akan selalu tegak lurus dengan cerminnya. Jika titik dicerminkan terhadap sumbu-x, maka garis penghubungnya tegak lurus terhadap sumbu-x. Jika titik dicerminkan terhadap sumbu-y, maka garis penghubungnya juga tegak lurus terhadap sumbu-y.
Rumus Umum Refleksi
-
Refleksi terhadap sumbu-x
Jika suatu titik (x,y) direfleksikan terhadap sumbu-x, maka koordinat y’ merupakan lawan dari koordinat y, sementara koordinat x tetap.
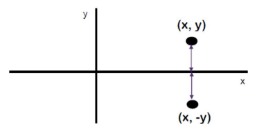
A(x,y) → P = A’(x,−y)
Keterangan:
A = titik A
A’ = hasil pencerminan dari titik A
x = titik yang terdapat pada sumbu-x
y = titik yang terdapat pada sumbu-y
P = pencerminan yang dilakukan terhadap sumbu-x
-
Refleksi terhadap sumbu-x
Sebaliknya, jika suatu titik (x,y) direfleksikan terhadap sumbu-y, maka koordinat x’ merupakan lawan dari koordinat x, sementara koordinat y tetap.
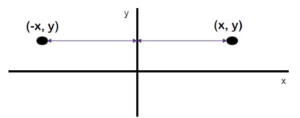
A(x,y) → P = A’(−x,y)
Keterangan:
A = titik A
A’ = hasil pencerminan dari titik A
x = titik yang terdapat pada sumbu-x
y = titik yang terdapat pada sumbu-y
P = pencerminan yang dilakukan terhadap sumbu-y
-
Refleksi terhadap garis y = x
Jika suatu titik A(x,y) direfleksikan terhadap garis y = x, maka hasil refleksinya adalah A'(y,x).
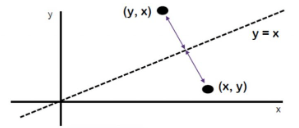
A(x,y) → P = A’(y,x)
Keterangan:
A = titik A
A’ = hasil pencerminan dari titik A
x = titik yang terdapat pada sumbu-x
y = titik yang terdapat pada sumbu-y
P = pencerminan yang dilakukan terhadap garis y = x
-
Refleksi terhadap garis y = -x
Jika suatu titik A(x,y) direfleksikan terhadap garis y = -x, maka hasil refleksinya adalah A'(-y,-x).
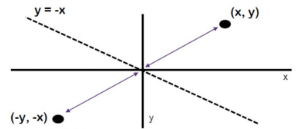
A(x,y) → P = A’(−y,−x)
Keterangan:
A = titik A
A’ = hasil pencerminan dari titik A
x = titik yang terdapat pada sumbu-x
y = titik yang terdapat pada sumbu-y
P = pencerminan yang dilakukan terhadap garis y = -x
-
Refleksi terhadap garis x = k
Jika titik A(x,y) direfleksikan terhadap garis x = k, maka hasil refleksinya adalah A'((2k-x),y).
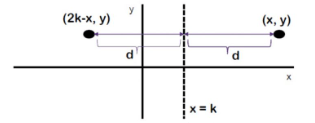
A(x,y) → P = A’((2k−x),y)
Keterangan:
A = titik A
A’ = hasil pencerminan dari titik A
x = titik yang terdapat pada sumbu-x
y = titik yang terdapat pada sumbu-y
P = pencerminan yang dilakukan terhadap garis x = k
-
Refleksi terhadap garis y = k
Jika titik A(x,y) direfleksikan terhadap garis y = k, maka hasil refleksinya adalah A'(x,(2k-y)).
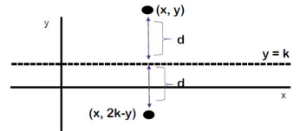
A(x,y) → P = A’(x,(2k−y))
Keterangan:
A = titik A
A’ = hasil pencerminan dari titik A
x = titik yang terdapat pada sumbu-x
y = titik yang terdapat pada sumbu-y
P = pencerminan yang dilakukan terhadap garis y = k\
Baca Juga: Cara Menyusun Persamaan Kuadrat dan Contohnya
Contoh Soal Refleksi
Berapakah hasil refleksi titik A(3,5) terhadap sumbu y?
Pembahasan:
Diketahui: A(3,5)
Ditanya: A’ terhadap sumbu-y …?
Jawab:
x = 3
y = 5
A(x,y) → P = A’(−x,y)
A(3,5) → P = A’(−3,5)
Jadi, hasil pencerminan titik A terhadap sumbu-y adalah A’(−3,5).
3. Rotasi (Perputaran)
Coba sebutin benda-benda yang berotasi?
Duh, banyak banget ya pasti. Ada jarum jam, roda kendaraan, sampai planet di angkasa juga berotasi. Nah, prinsip jenis transformasi ini sebenarnya sama ya dengan benda-benda yang berputar di sekeliling kita.
Rotasi adalah perubahan posisi suatu titik atau bidang dengan cara diputar dengan sudut tertentu. Ini nih yang khas dari rotasi, dia berpatokan pada sudut untuk mengubah posisi titiknya. Sudut yang dipakai biasanya sudut 90°, 180°, dan 270°.
Harus diinget, setiap terjadi rotasi, ukuran dan bentuk bidangnya akan selalu sama, nggak berubah-ubah ya. Tapi, kamu juga harus perhatikan unsur dari rotasi. Apa sih unsur-unsur rotasi itu?
Sifat-Sifat Rotasi
- Rotasi memiliki arah dan besar sudut,
- Jika diputar searah jarum jam, sudut akan bernilai negatif,
- Jika diputar berlawanan arah jarum jam, sudut bernilai positif. Jangan kebalik ya!
Rumus Umum Rotasi
Secara umum, rotasi suatu titik dibagi menjadi dua, yakni rotasi terhadap titik pusat (0,0) dan rotasi terhadap titik (a,b).
Namun, pada tingkatan ini, kita hanya akan membahas rotasi terhadap titik pusat (0,0) dulu, ya. Nanti deh kalo kamu sudah berada di bangku SMA, baru akan belajar materi yang lebih lanjut.
| Titik Asal | Rotasi | Titik Bayangan |
| (x,y) | (0,90°) | (-y,x) |
| (x,y) | (0,-90°) | (y,-x) |
| (x,y) | (0,180°) | (-x,-y) |
| (x,y) | (0,-180°) | (-x,-y) |
| (x,y) | (0,270°) | (y,-x) |
| (x,y) | (0,-270°) | (-y,x) |
Catatan: Sudut positif menandakan rotasi berlawanan jarum jam, sedangkan sudut negatif menandakan rotasi searah jarum jam.
Contoh Soal Rotasi
Segiempat PQRS berkoordinat di titik P(2,-2), Q(4,-1), R(4,-3), dan S(2,-4). Tentukan bayangan segiempat PQRS pada rotasi 90° berlawanan arah jarum jam yang berpusat di titik asal O(0,0)!
Pembahasan:
Rotasi 90° berlawanan arah jarum jam yang berpusat di titik asal O(0,0), maka
(x,y) O,90° → (-y,x)
- Titik P(2,-2) O,90° → P'(2,2)
- Titik Q(4,-1) O,90° → Q'(1,4)
- Titik R(4,-3) O,90° → R'(3,4)
- Titik S(2,-4) O,90° → S'(4,2)
Sehingga, diperoleh titik-titik bayangannya adalah P(2,-2), Q(1,4), R(3,4), dan S(4,2).
Baca Juga: 3 Cara Mudah Menyelesaikan Persamaan Kuadrat
4. Dilatasi
Biasanya saat listrik di rumah padam, terus kamu nyalain senter dan mengarahkan ke tangan, pasti ada bayangan yang terbentuk. Bayangannya berukuran lebih besar dari tangan kita normalnya.
Nah, tanpa disadari perilaku kita itu berkaitan dengan dilatasi, atau bisa dibilang tangan kita didilatasi. Wihh kedengarannya matematis banget tuh ya, hahaha!
Tau nggak sih? dilatasi itu jenis transformasi yang paling beda dari ketiga jenis transformasi lainnya. Hmm, kira-kira apa yang bikin beda, nih?
Dari segi definisinya aja, dilatasi adalah suatu transformasi yang mengubah ukuran suatu objek atau benda, bisa memperbesar atau memperkecil. Kalo jenis transformasi sebelumnya kan yang berubah hanya posisinya, nah kalo hasil dari dilatasi posisi sama ukurannya yang berubah. Eits, tapi bentuknya tetap sama ya.
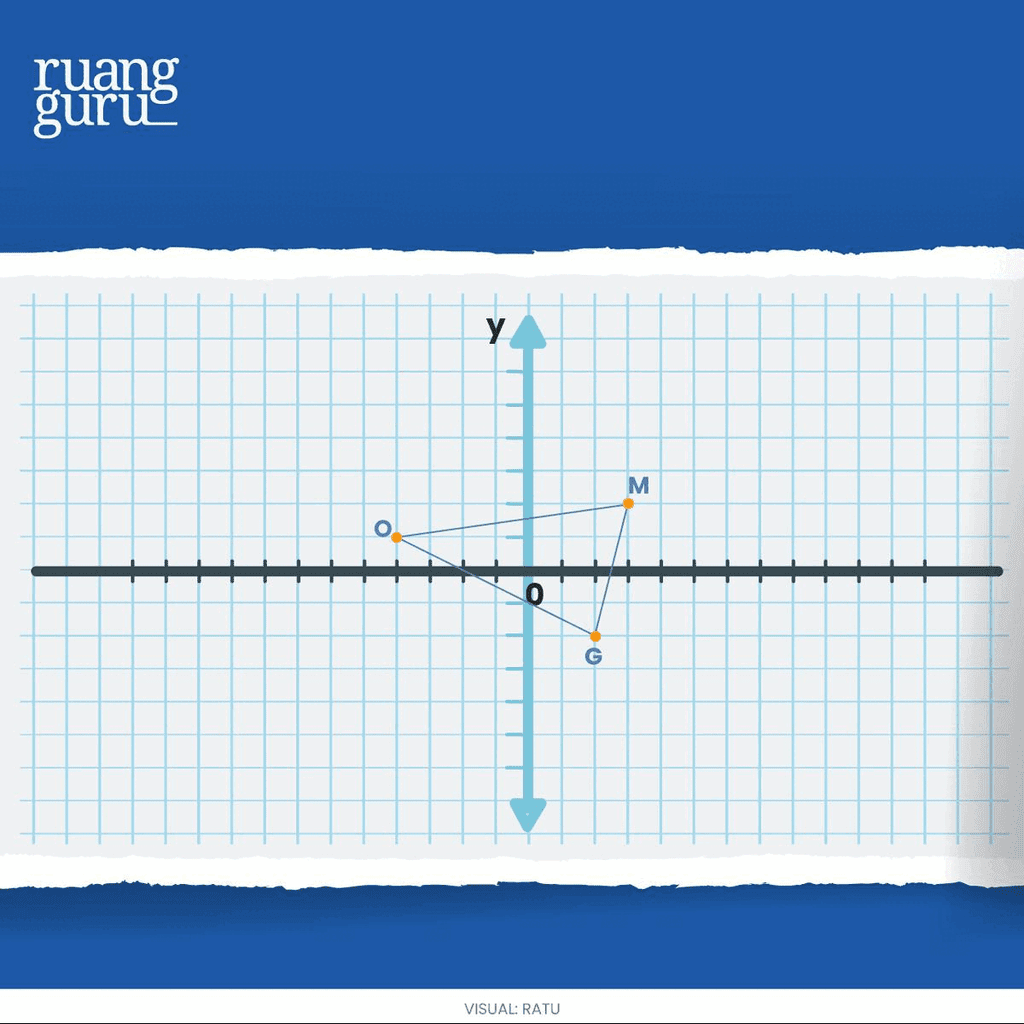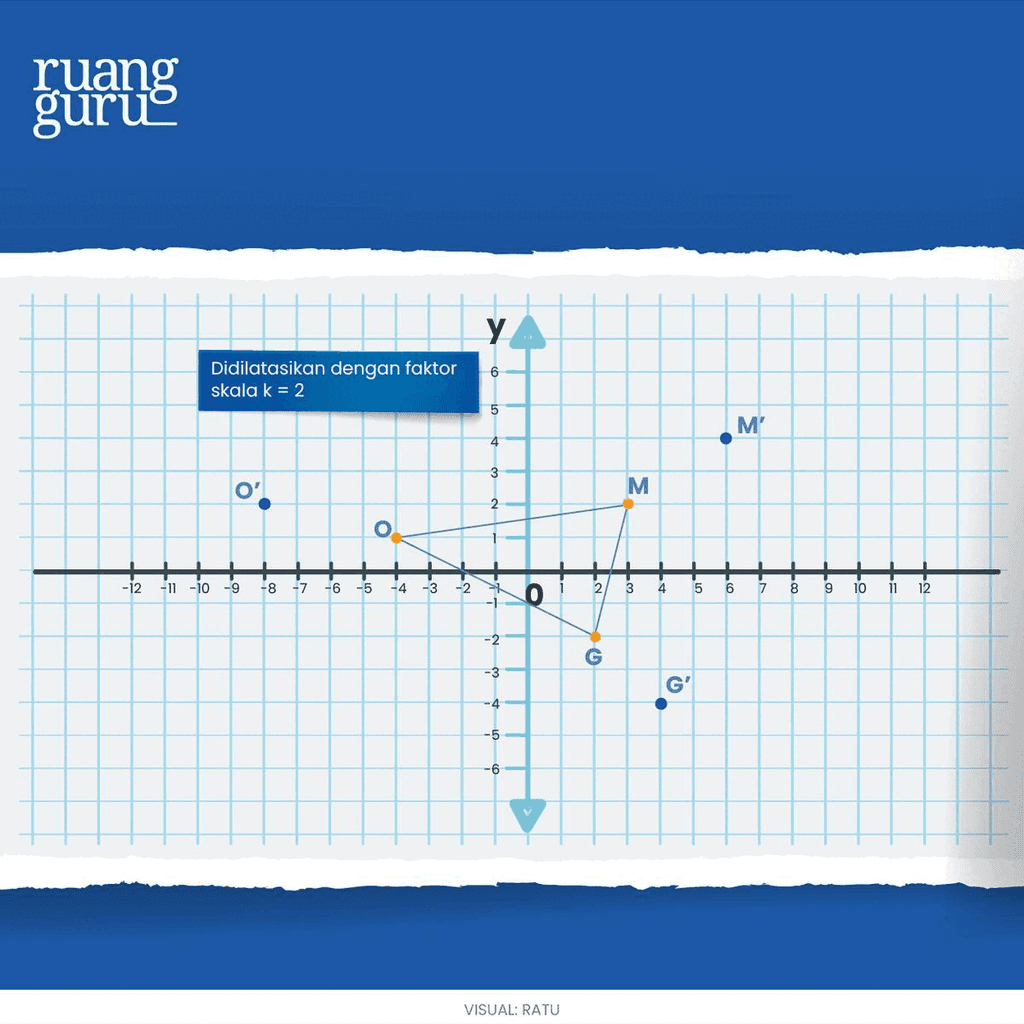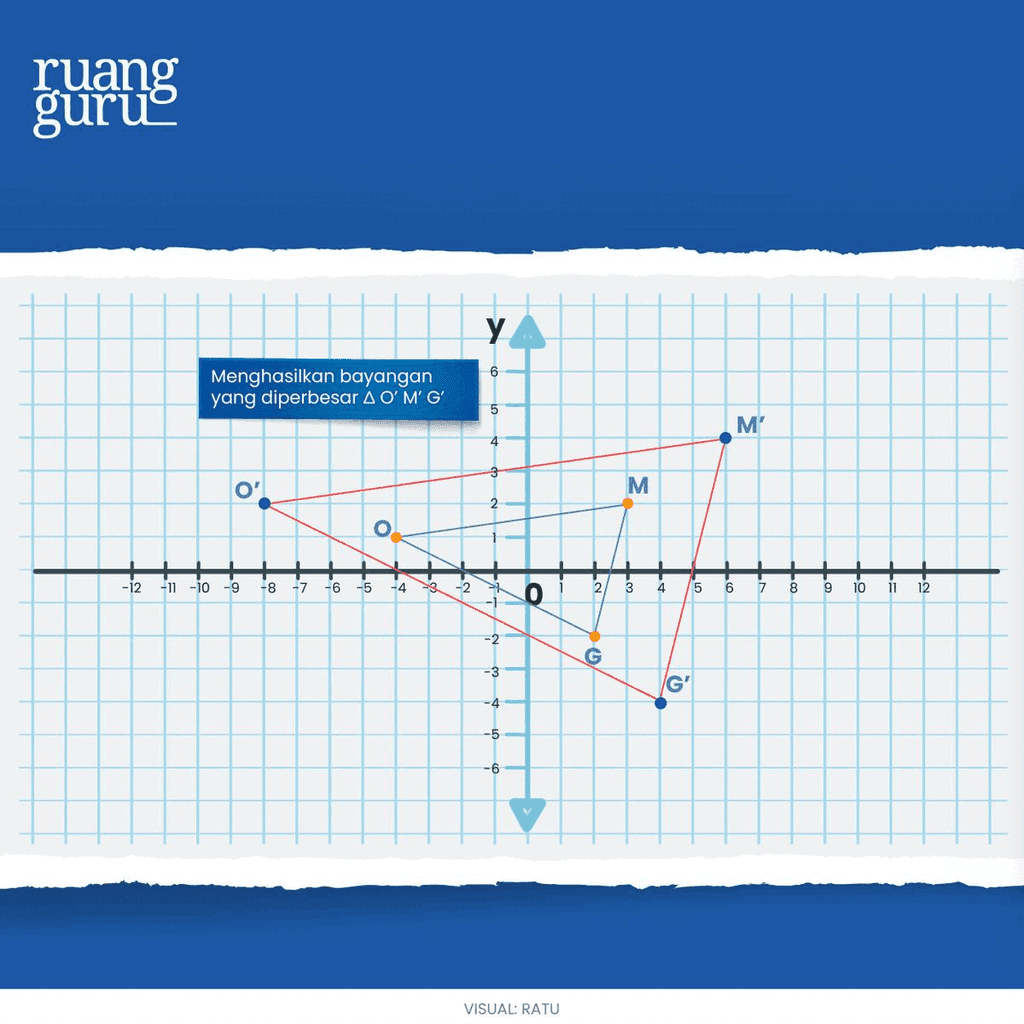
Unsur-Unsur Dilatasi
Unsur dilatasi yang harus kamu perhatikan, ada 2 nih:
1. Pusat dilatasi atau titik acuan
Kalo dari ilustrasi di awal tadi sih, senter itu adalah pusat dilatasinya.
2. Faktor skala biasa disimbolkan dengan k
Maksudnya adalah faktor yang menyebabkan hasil dilatasi memperbesar atau memperkecil objek aslinya.
Rumus Umum Dilatasi
Kamu bisa liat rumusnya di bawah ini ya! Kamu pahami dulu, nanti kita bahas soal-soal dari jenis transformasi ini:

Contoh Soal Dilatasi
Titik A(1,3) akan didilatasikan sebesar tiga kali, dengan pusat yang berada di (-3,1). Tentukanlah bayangan titik A setelah didilatasikan!
Pembahasan:
Diketahui:
k = 3
x = 1, y = 3
a = -3, b = 1
Ditanya: A’ … ?
Jawab:
A(x, y) = A'(k(x-a) + a, k(y – b) + b)
A(1, 3) = A'(3(1 – (-3)) + (-3), 3(3 – 1) + 1)
A(1, 3) = A'(3(1 + 3) – 3, 3(2) + 1)
A(1,3) = A'(3(4) – 3, 6 + 1)
A(1,3) = A'(12 – 3, 6 + 1)
A(1,3) = A'(9,7)
Maka letak titik A’ dari koordinat (1,3) dengan dilatasi sebesar tiga kali yang berada di titik pusat (-3,1) adalah (9,7).
—
Keempat jenis transformasi udah dibahas. Menurut kamu yang paling seru yang mana nih? Eits, tapi sesuai janji aku tadi, kita bahas soal HOTS yuk, supaya kamu paham untuk penggunaan rumus-rumus tadi.
Baca Juga: Ketahui Sifat-Sifat Bentuk Akar & Cara Merasionalkannya
Contoh Soal Transformasi Geometri
Titik A(2,1) direfleksikan terhadap garis y = 3. Kemudian, dilatasi terhadap pusat (1,2) dengan faktor skala -2. Selanjutnya, dirotasi 180 derajat dengan pusat O(0,0). Bayangan titik A adalah…
- A’’’(-1,4)
- A’’’(-1,-4)
- A’’’(1,4)
- A’’’(1,-4)
Nah, karena di awal kita sudah banyak mengerjakan soal-soal transformasi geometri, boleh dong yang ini kamu kerjakan mandiri sebagai bahan latihan. hehehe… Kalo sudah ketemu jawabannya, bisa tulis di kolom komentar, ya!
Buat kamu yang masih gemes untuk ngerjain soal-soal seru lainnya langsung gabung aja deh ke ruangbelajar. Soal-soalnya selalu upgrade plus ada pembahasan soalnya juga. Sampai ketemu di artikel selanjutnya, dadah!
Referensi:
Subchan. Winarni. Mufid, M. S. dkk. (2018) Matematika. Jakarta: Kemendikbud.















