Cara Menyusun Persamaan Kuadrat dan Contohnya | Matematika Kelas 9

Di artikel sebelumnya, kita sudah belajar cara mencari akar-akar dari persamaan kuadrat. Masih ingat nggak dengan bentuk umum persamaan kuadrat? Yup! Bentuk umum persamaan kuadrat adalah

ax² + bx + c = 0

dengan a, b, c merupakan bilangan real dan a ≠ 0

Nah, kali ini kebalikannya, nih. Kita akan belajar cara menyusun persamaan kuadrat dari akar-akar yang diketahui. Wah, gimana tuh caranya? Oke, daripada penasaran, yuk simak artikel berikut ini!

Ada dua metode untuk menyusun persamaan kuadrat. Metode yang pertama, jika diketahui akar-akar persamaan kuadratnya. Lalu, metode yang kedua, jika diketahui jumlah dan hasil kali dari akar-akar persamaan kuadratnya. Nanti pas ngerjain soal, kamu pilih deh pakai metode yang mana, menyesuaikan dengan yang diketahui di soal.

1. Cara Menyusun Persamaan Kuadrat Jika Diketahui Akar-akarnya

Misalnya, diketahui akar-akar persamaan kuadrat adalah x₁ dan x₂. Untuk mendapatkan persamaan kuadratnya, kamu bisa substitusi akar-akar tersebut ke persamaan berikut:

Baca juga: Cara Menghitung Luas dan Volume Kerucut

Kenapa sih harus disubstitusi ke persamaan itu? Kamu masih ingat nggak, kalau ingin mendapatkan akar-akar dari suatu persamaan kuadrat, salah satu caranya adalah dengan memfaktorkan persamaan kuadrat tersebut. Nah, bentuk persamaan (x – x₁)(x – x₂) = 0 adalah hasil dari pemfaktoran persamaan kuadrat. Kalau kita lakukan sedikit operasi aljabar, kita kali silang persamaan itu, maka akan didapat suatu persamaan kuadrat.

Oke, supaya lebih paham, perhatikan contoh soal di bawah ini, yuk!

Contoh soal 1

Tentukan persamaan kuadrat yang akar-akarnya adalah 3 dan -7.

Penyelesaian:

Diketahui akar-akar persamaan kuadrat adalah 3 dan -7. Berarti, kamu bisa tulis x₁ = 3 dan x₂ = -7. Kemudian, kedua akar tersebut bisa kamu substitusikan ke persamaan (x – x₁)(x – x₂) = 0, sehingga penyelesaiannya menjadi sebagai berikut:

(x – 3)(x – (-7)) = 0

(x – 3)(x + 7) = 0

x² + 7x – 3x – 21 = 0

x² + 4x – 21 = 0

Jadiii, persamaan kuadrat yang akar-akarnya 3 dan -7 adalah x² + 4x – 21 = 0.

Gimana gengs, mudah bukan caranya? Cukup dengan mensubstitusi nilai akar-akarnya dan sedikit melakukan operasi aljabar, kamu sudah bisa mendapatkan persamaan kuadratnya. Yuk, kita lanjut ke metode kedua, ya!

2. Cara Menyusun Persamaan Kuadrat Jika Diketahui Jumlah dan Hasil Kali Akar-akarnya

Misalkan, akar-akar suatu persamaan kuadrat adalah x₁ dan x₂. Jika yang diketahui pada soal adalah jumlah dan hasil kali akar-akarnya, maka untuk mendapatkan persamaan kuadratnya, kamu bisa gunakan rumus berikut ini:

Nah, sebenarnya, bentuk persamaan x² – (x₁ + x₂)x + (x₁ . x₂) = 0 merupakan hasil kali silang dari persamaan (x – x₁)(x – x₂) = 0, yang kita gunakan untuk mencari persamaan kuadrat di metode sebelumnya. Penjabarannya, bisa kamu lihat pada gambar di bawah ini, nih.

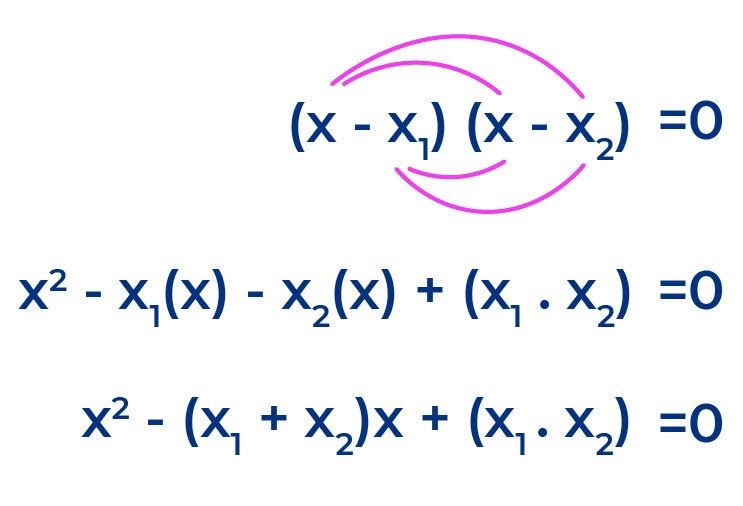
Terus, kenapa sih bisa dapat x₁ + x₂= -b/a dan x₁ . x₂ = c/a? Berawal dari persamaan x² – (x₁ + x₂)x + (x₁ . x₂) = 0, kemudian masing-masing ruas dikalikan dengan konstanta a, sehingga persamaan tersebut menjadi sebagai berikut:

ax² – a(x₁ + x₂)x + a(x₁ . x₂) = 0

Setelah itu, disamain deh dengan bentuk umum persamaan kuadrat, sehingga diperoleh:

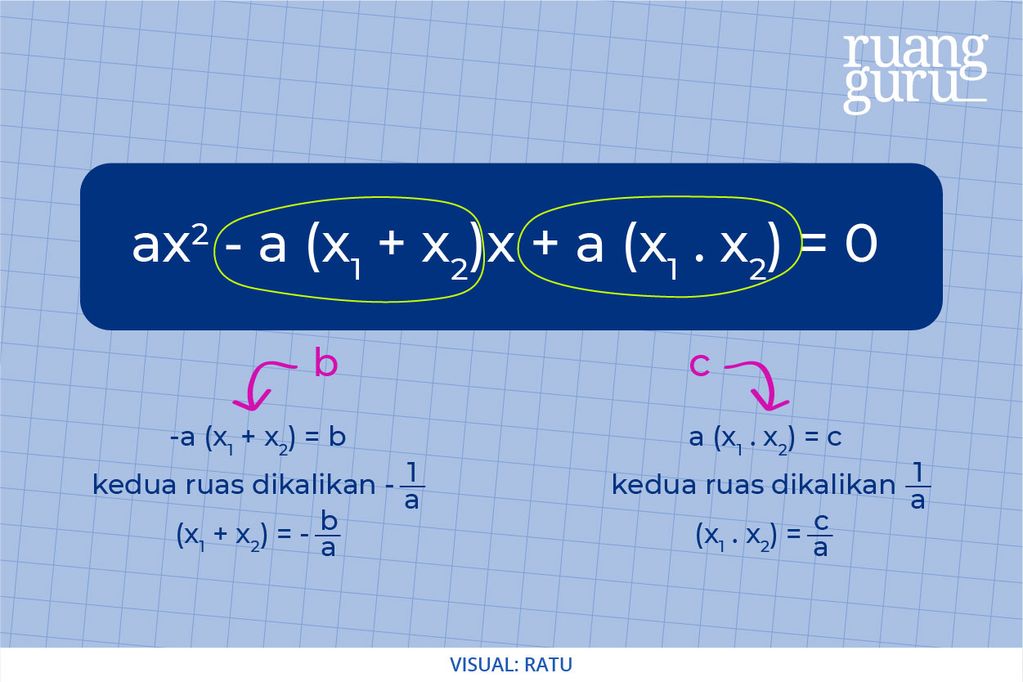
Dari penjabaran itu lah rumus hasil jumlah dan kali akar-akar persamaan kuadrat berasal. Gimana, sudah paham ya dengan konsep rumusnya? Oke, sekarang, kita perhatikan contoh soal dibawah ini, ya!

Contoh soal 2

Tentukan persaman kuadrat yang akar-akarnya adalah α dan β, serta jumlah dan hasil kali akar-akarnya adalah -1 dan -20.

Penyelesaian:

Diketahui akar-akarnya adalah x₁ dan x₂. Kemudian, hasil jumlah akar-akarnya adalah -1, berarti x₁ + x₂ = -1. Lalu, hasil kali akar-akarnya adalah -20, berarti x₁ . x₂ = – 20. Nah, kamu bisa langsung substitusi hasil jumlah dan kali akar-akar yang sudah diketahui ke persamaan:

x² – (x₁ + x₂)x + (x₁ . x₂) = 0

Sehingga persamaannya menjadi seperti berikut:

x² – (-1)x + (-20) = 0

x² + x – 20 = 0

Jadi, diperoleh persamaan kuadratnya adalah x² + x -20 = 0.

Baca Juga: Cara Menghitung Luas dan Volume Bola

Contoh soal 3

Susunlah persamaan kuadrat yang akar-akarnya 3 kali akar-akar persamaan persamaan kuadrat 2x² + 5x – 3 = 0.

Penyelesaian:

Karena akar persamaan kuadrat yang baru adalah transformasi akar persamaan kuadrat yang lama, kita bisa gunakan metode substitusi.

Apa sih maksudnya transformasi? Maksudnya, dua-duanya berubahnya sama gitu. Di sini, kedua akarnya sama-sama 3 kali akar-akar yang lama.

Biar nggak bingung, kita pakai variabel p untuk persamaan kuadrat yang baru.

Nah, jadinya p = 3x atau kalau kita mau x dalam p, jadinya x = 1/3 p.

Langsung aja kita substitusiin ya,

2x² + 5x – 3 = 0

2(1/3p)² + 5(1/3p) – 3 = 0

2/9p² + 5/3p – 3 = 0

kedua ruas kita kalikan dengan 9

2p² + 15p – 27 = 0

Sehingga, persamaan kuadrat baru yang akar-akarnya 3 kali persamaan kuadrat 2x² + 5x – 3 = 0 adalah 2p² + 15p – 27 = 0.

Kalau mau ditulis lagi dalam x juga nggak papa. Jadinya,  2x² + 15x – 27 = 0.

Contoh soal 4 

Diketahui akar-akar persamaan kuadrat x² + qx + r = 0 adalah x₁ dan x₂, dimana x₁ < x₂. Tentukan persamaan kuadrat dengan akar x₁ + 2 dan x₂ – 2.

Penyelesaian:

Nah, kalau soalnya kayak gini, nggak bisa pake metode substitusi tadi. Soalnya, x₁ dan x₂ berubahnya beda. Ada yang ditambah 2, ada yang dikurangi 2.

Terus, gimana, dong? Tenang.

Akar-akar persamaan kuadrat x² + 3x -10 = 0 adalah x₁ dan x₂. Kita langsung faktorin aja persamaan kuadratnya, ya. Jadinya,

x² + 3x -10 = 0

(x-2)(x+5) = 0

Sehingga, diperoleh akar-akarnya, yaitu x = -5 atau x = 2.

Nah, di soal diketahui kalau x₁ < x₂. Akar yang lebih kecil yang mana? -5 kan ya. Jadi, x₁ = -5 dan x₂ = 2.

Untuk mencari persamaan kuadrat yang barunya, kita bisa gunakan rumus (x – x₁)(x – x₂) = 0. Karena diketahui di soal kalau akar-akarnya x₁ + 2 dan x₂ – 2, berarti: 

[x – (x₁ + 2)][x – (x₂ – 2)]=0 

Kita substitusi nilai x₁ dan x₂ yang kita dapatkan barusan, sehingga:

[x – (-5 + 2)][x – (2 – 2)]=0 

(x-(-3))(x-0) = 0

(x+3)(x) = 0

kita kali silang

x² + 3x = 0

Jadi, persamaan kuadrat dengan akar x₁ + 2 dan x₂ – 2 adalah x² + 3x = 0. 

Oke, contoh soalnya sudah ada empat, nih. Bisa dong sekarang kalau diminta menyusun persamaan kuadrat. Huehehe…

Gengs, sadar nggak sih, salah satu kunci agar pandai dalam matematika itu adalah banyak mengerjakan latihan soal. Dengan begitu, logika berpikir kamu akan semakin terasah, rumus-rumus yang sering digunakan pun akan melekat di otak kamu dengan sendirinya. Selain itu, kamu juga bisa bertemu dengan berbagai macam variasi soal. Jadi, pemahaman materi kamu akan semakin dalam.

Nah, kamu bisa lho cobain latihan berbagai macam soal di ruangbelajar. Di sana latihan soalnya lengkap dan ada pembahasannya juga. So, tunggu apa lagi? Buruan gabung sekarang juga!

Sumber Referensi:

Wagiyo, A. Mulyono, S. and Susanto, (2008) Pegangan Belajar Matematika 3. Jakarta: Pusat Perbukuan, Departemen Pendidikan Nasional.