Ketahui Sifat-Sifat Bentuk Akar & Cara Merasionalkannya | Matematika Kelas 9

Artikel Matematika kelas 9 ini menjelaskan tentang bentuk akar dalam matematika, meliputi pengertian, sifat-sifat, dan cara merasionalkannya.

—

Apa yang terlintas dalam pikiranmu saat mendengar kata akar? Mungkin kamu membayangkan sebuah pohon yang ditopang oleh akar yang kokoh. Tapi, adakah di antara kamu yang terpikir akar dalam bentuk matematika? Nah, yang akan kita bahas kali ini adalah bentuk akar dalam matematika, ya. Lalu, apa yang dimaksud dengan bentuk akar itu?

Dalam matematika, bentuk akar merupakan suatu operasi aljabar yang dapat digunakan untuk menyelesaikan masalah bilangan. Bentuk akar memiliki sifat-sifat khusus dan dapat dirasionalkan. Apa saja sifat-sifat itu dan bagaimana cara merasionalkan bentuk akar? Simak penjelasan berikut, yuk!

Mengenal Bentuk Akar

Bentuk akar adalah akar dari suatu bilangan rasional yang hasilnya berupa bilangan irasional. Hayo, kamu masih ingat nggak nih dengan bilangan rasional dan irasional? Kalo lupa, bisa baca-baca artikelnya di link ini, ya. Bentuk akar merupakan bentuk lain untuk menyatakan bilangan berpangkat pecahan. Bilangan bentuk akar akan berada dalam tanda “√”, atau bisa kita sebut sebagai tanda akar. 

Aku kasih contoh deh biar kamu nggak bingung. Misalnya, ada bilangan berpangkat 2^1/2. Nah, bilangan berpangkat 2^1/2 kalo kita ubah ke bentuk akar, jadinya akan seperti ini:

2^1/2  (a = 2, m = 1, n = 2)

2^1/2 = atau √2

Fyi nih, kalo indeks akarnya bernilai 2, nggak perlu kamu tulis juga nggak papa, ya.

Contoh bentuk akar yang lain di antaranya √6, √7, √11, 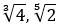 dan masih banyak lagi. Coba aku tanya, √25 itu termasuk bentuk akar atau bukan, sih? Eits! Jawabannya bukan bentuk akar. Kenapa? Ingat definisinya, bentuk akar itu berupa bilangan irasional, sedangkan √25 bisa kita sederhanakan menjadi √5² = 5^2/2 = 5 (5 adalah bilangan rasional). Jadi, √25 bukan bentuk akar. Paham, ya?

Baca Juga: Cara Menyelesaikan Persamaan Kuadrat

Sifat-Sifat Bentuk Akar

Seperti halnya bilangan berpangkat, bilangan bentuk akar juga memiliki sifat-sifat tertentu, lho! Sifat-sifat ini akan memudahkan kita dalam melakukan operasi aljabar yang melibatkan bentuk akar nantinya. Sifat-sifat bentuk akar, di antaranya sebagai berikut:

Nah, setelah kamu mengetahui maksud dari bentuk akar dan sifat-sifatnya, selanjutnya, kita ketahui cara merasionalkan bentuk akar, yuk! Sebeneranya, merasionalkan bentuk akar tuh apa, sih?

Cara Merasionalkan Bentuk Akar

Untuk memudahkan penggunaan bentuk akar dalam operasi aljabar, bentuk akar harus ditulis dalam bentuk yang paling rasional (sederhana). Cara merasionalkan bentuk akar harus memenuhi syarat-syarat tertentu. Syarat-syarat tersebut antara lain sebagai berikut:

Terus, gimana nih kalo misalnya kita menemukan bentuk yang belum sederhana? Gimana cara menyederhanakan bentuk tersebut? Oke, tenang-tenang, aku bakal jelasin caranya di bawah ini.

Kasus 1: Jika bilangan pokok memiliki pangkat lebih besar dari indeks akarnya.

Nah, kalo kamu menemukan bentuk yang kayak gitu, dan bilangan pokoknya itu bernilai positif, maka kamu bisa jabarkan aja bentuk pangkatnya.

Contoh 1: √x⁵

Bentuk akar √x⁵ belum sederhana karena pangkat bilangan pokoknya atau pangkat si x lebih besar dari indeks akarnya (5 > 2). Jadi, untuk menyederhanakan bentuk tersebut, kita jabarkan aja pangkat si x nya.

Karena, indeks akarnya itu bernilai 2, maka bisa kita jabarkan kayak gini:

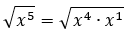
Ingat sifat bentuk akar, ya! Kalo ada operasi perkalian dalam akar, bisa kita pecah jadi seperti ini:

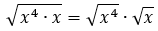
Nah, √x⁴ itu sama aja dengan x^4/2, sehingga bisa disederhanakan menjadi x². Jadi,

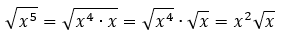
Gimana, paham ya cara menyederhanakannya? Contoh lagi, deh!

Baca Juga: Cara Menyusun Persamaan Kuadrat dan Contohnya

Contoh 2: √20

Kurang lebih cara penyederhanaannya sama kayak contoh 1 kok, teman-teman. Penjabarannya kayak gini,

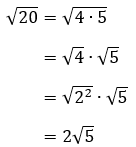
Itu cara penyederhanaan untuk kasus pertama, ya. Sekarang, kita masuk ke kasus kedua.

Kasus 2: Pada bilangan pecahan, terdapat akar di bagian penyebut.

Kalo kamu menemukan bentuk seperti itu, kamu bisa menyederhanakannya dengan mengalikan bilangan pecahan tersebut dengan bentuk akar yang sekawan dari penyebutnya. Maksudnya bentuk akar yang sekawan tuh gimana, ya? Bentuk akar sekawan itu berarti bentuk akarnya sama, cuma beda tanda operasinya aja. Nah, penjelasan lebih lengkapnya bisa kamu lihat pada gambar di bawah ini!

Biar lebih paham, kita masuk ke contoh soal, ya!

Contoh Soal Bentuk Akar

Contoh: Sederhanakan bentuk akar !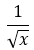

Untuk menyederhanakan bentuk akar tersebut, kita bisa kalikan dengan bentuk akar yang sekawan dari penyebutnya. Karena penyebutnya itu √x, berarti bentuk sekawannya juga √x. Jadi, penyelesaiannya akan seperti ini,

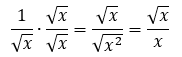
Sudah paham? Kalo gitu, kita masuk ke kasus terakhir.

Kasus 3: Jika di dalam akar memuat bilangan pecahan.

Waduh, gimana nih kalo misalnya kita menemukan soal yang bentuknya kayak gitu? Tenang, kamu masih ingat dengan sifat bentuk akar di atas, kan? Kalo ada pecahan di dalam akar, maka bisa kita jabarkan kayak gini,

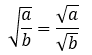
Nah, karena setelah dijabarkan bentuknya menjadi seperti kasus nomer 2 (ada akar di penyebut), jadi langkah selanjutnya bisa kita selesaikan seperti kasus nomer 2, teman-teman. Yup! Betul sekali, kita kalikan dengan bentuk akar sekawan penyebutnya. Langsung masuk ke contoh soal aja, deh.

Contoh: Rasionalkan bentuk akar !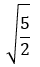

Sesuai penjabaran di atas, kita pecah dulu ya bentuk akarnya jadi seperti ini,

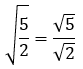
Kemudian, kita kalikan dengan bentuk akar sekawan pada penyebutnya. Ingat, pada penyebutnya loh ya, bukan pembilang. Sehingga,

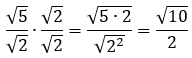
Begitu teman-teman cara merasionalkannya. Sudah paham belum nih sampai sini?

Oke, supaya kamu bisa lebih menguasai materi ini, berikut aku kasih beberapa contoh soal. Bisa kamu kerjakan sendiri atau diskusi dengan teman sekolahmu, ya!

Latihan Soal Bentuk Akar

Sederhanakanlah bentuk akar berikut ini:

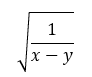
Nah, itulah penjelasan mengenai pengertian bentuk akar dalam matematika, sifat-sifat, dan cara merasionalkannya. Jangan lupa untuk terus berlatih soal-soal, ya. Kalo kamu masih ingin mempelajari lagi materi ini, langsung aja gunakan ruangbelajar. Kamu bisa belajar sambil menonton video animasi lengkap dengan soal, pembahasan, dan rangkumannya. Yuk, belajar jadi hebat dengan Ruangguru!

Referensi:

Subchan, Winarni, Hanafi L, dkk. (2015) Matematika SMP/MTs Kelas IX Semester 1. Jakarta: Kementerian Pendidikan dan Kebudayaan

Artikel ini pertama kali dibuat oleh Karina Dwi Adistiana dan diperbarui oleh Hani Ammariah pada 27 Juli 2021.