Cara Menghitung Luas Permukaan dan Volume Gabungan Bangun Ruang Sisi Lengkung | Matematika Kelas 9

Kalau menghitung luas dan volume suatu bangun ruang itu mah udah biasa ya. Tapi kalo bangun-bangun tersebut digabungkan, luas dan volumenya seperti apa, ya? Yuk, cek di sini!

 —

Hai gengs, wih kalo udah klik artikel ini, berarti kamu udah selesai belajar konsep masing-masing bangun ruang sisi lengkung, ya?

Inget loh, syarat utama supaya kamu bisa menghitung gabungan luas dan volume bangun ruang sisi lengkung adalah paham konsep masing-masing bangun ruang sisi lengkung itu sendiri. 

Bangun ruang sisi lengkung yang udah kita bahas kan ada tabung, kerucut, dan bola. Jadi, untuk paham konsep dari bangun itu semua gak susah kok guys, apalagi rumus luas dan volumenya berkaitan, jadi makin gampang kan buat nempel di otaknya.

Eits, tapi gapapa banget kalo kamu mau baca-baca dulu konsep dari ketiga bangun ruang sisi lengkung ini.  Aku setia nungguin kamu kok, tapi jangan lupa balik lagi ya wehehe.

(Sumber: Giphy.com)

Nah, setelah kamu udah paham betul konsepnya, nih aku kasih bonus tabel rumusnya.

Baca juga: Cara Menyusun Persamaan Kuadrat

Rumus-Rumus Bangun Ruang Sisi Lengkung

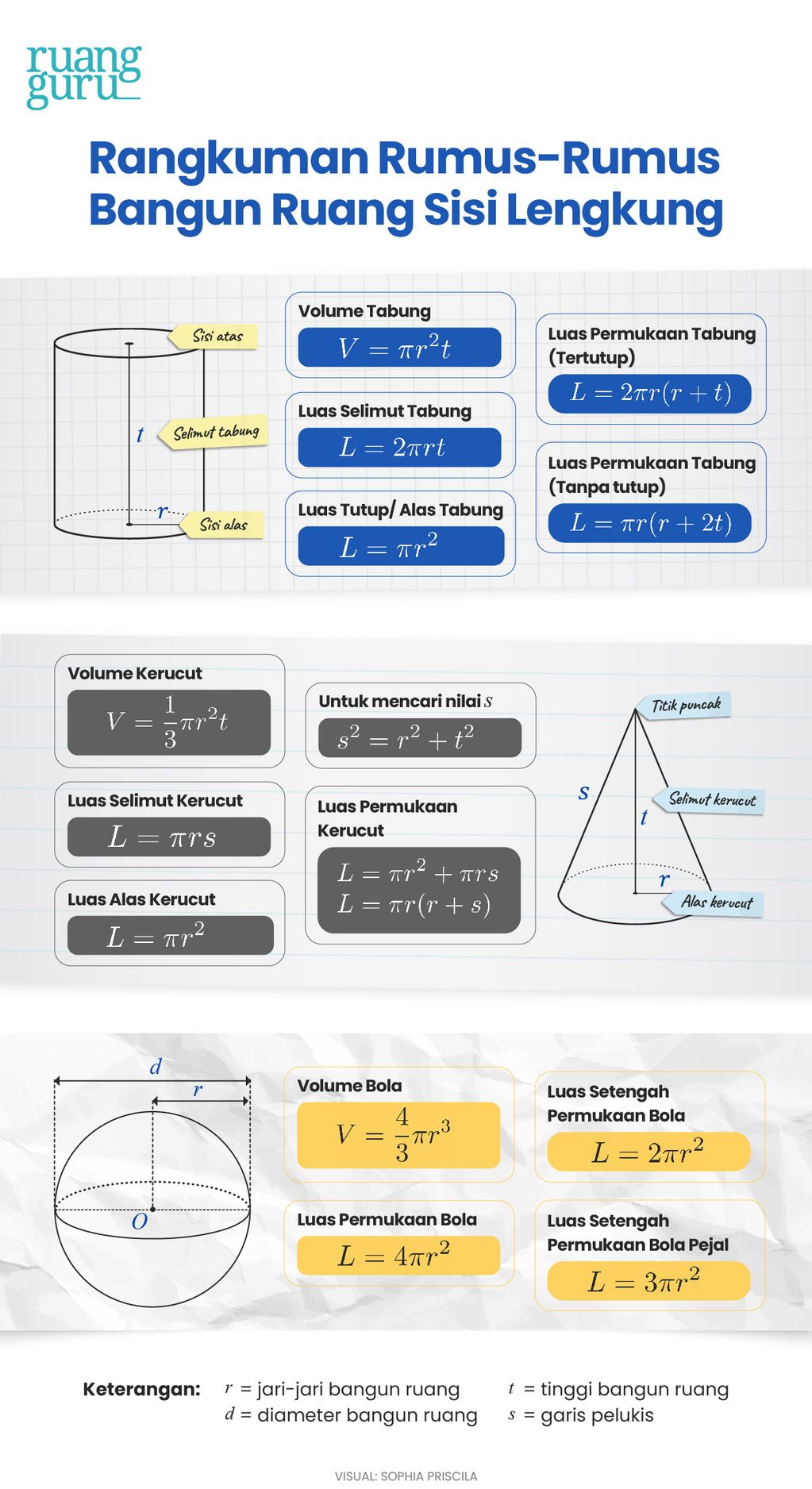
Konsep Gabungan Bangun Ruang Sisi Lengkung

Sekarang kita fokus ke gabungan bangun ruang sisi lengkung. Coba deh liat dan jawab pertanyaan dari gambar di bawah!

Untuk bagian A, B, dan C, pasti bisa kamu jawab dengan benar. Tapi untuk gambar yang d, pasti ada juga yang bingung, ayo ngaku hehehe! Well, gambar D itu lah yang disebut gabungan bangun ruang sisi lengkung. Karena dia tersusun dari beberapa bangun ruang sisi lengkung, yaitu tabung tanpa tutup di bagian bawah dan kerucut tanpa atas di bagian atas. 

Baca juga: Apa Bedanya Kongruen dan Sebangun pada Bangun Datar?

Contoh gabungan bangun ruang sisi lengkung di sekitar kita banyak banget loh. Misalnya, tenda sirkus, pensil, obat kapsul, tabung reaksi, pajangan, dan masih banyak lagi.

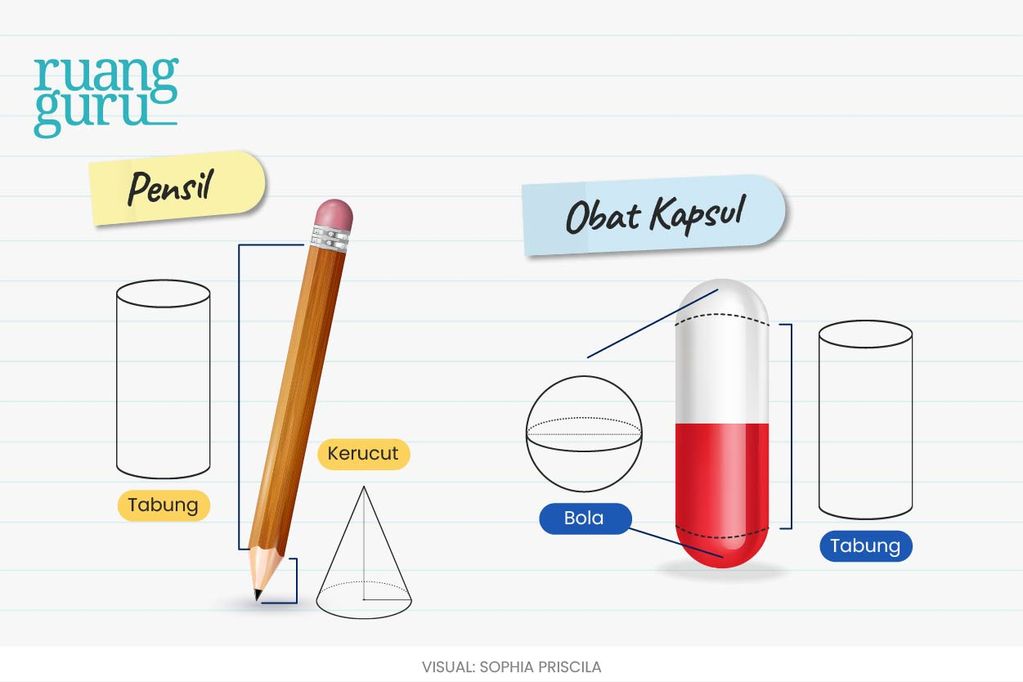
Pokoknya, buat kamu yang tadi bingung, mulai sekarang gak boleh bingung lagi ya! 

Nah, sebelum masuk ke pembahasan soal, ada tips sedikit nih dari aku. Jadi, untuk menghitung luas dan volume gabungan bangun ruang sisi lengkung, kamu wajib bisa menganalisis dan membayangkan bangunnya. Contohnya, bangun tersebut punya tutup/alas atau tidak. Tujuannya, supaya kamu nggak salah ngitung. Oke, kalo gitu kita langsung aja masuk ke soal yang pertama.

Contoh Soal Gabungan Bangun Ruang Sisi Lengkung

Soal 1

Penyelesaian:

Tabung reaksi terbentuk dari gabungan tabung dan setengah bola. Tapi, kamu wajib analisis kedua bangun itu lebih lanjut nih. Tabung tersebut nggak ada tutup alasnya kan, makanya yang kita cari adalah selimut tabungnya. Terus, untuk setengah bola juga nggak ada tutupnya atau disebut dengan bola berongga.

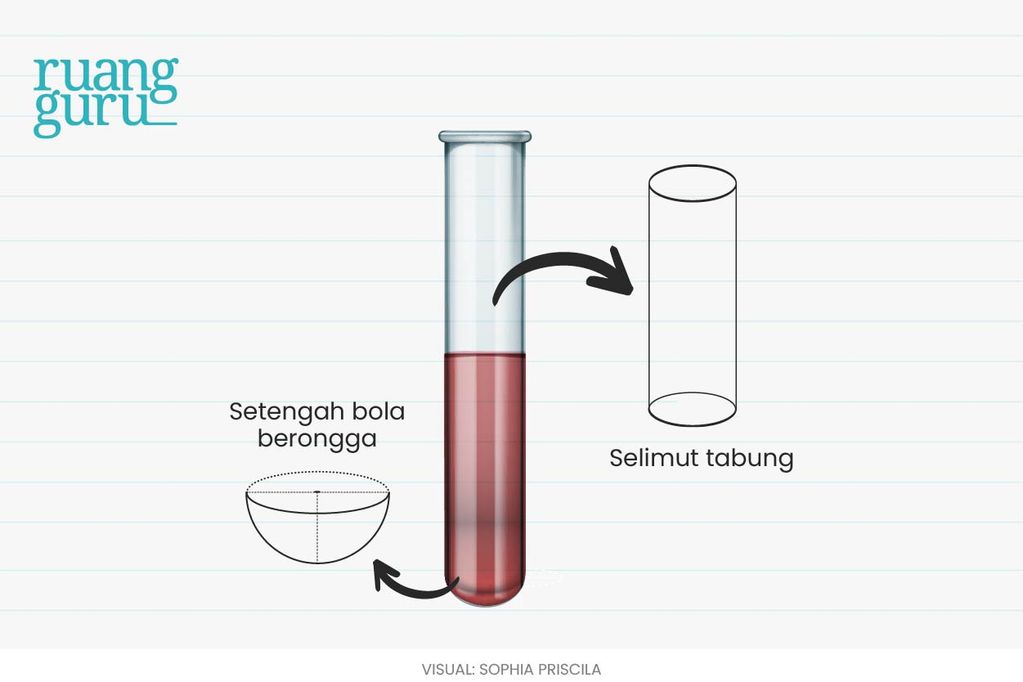
Diketahui:

diameter = 16 mm r = 8 mm

Yang ditanya Luas permukaan, maka rumusnya adalah

Luas permukaan tabung reaksi = luas selimut tabung + luas selimut setengah bola

• Sebelum mencari luas selimut tabung, kita cari dulu tinggi tabung.
  Tinggi tabung = tinggi keseluruhan – jari-jari setengah bola
                                = 150mm – 8mm
                                = 142 mm

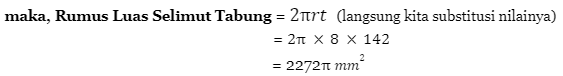
Inget ya guys, karena dalam pilihan ganda (PG) di soal ini tetap, jadi kita nggak perlu ubah ke bentuk bilangan (22/7 atau 3,14).  

• Next, cari luas selimut setengah bola.

Maka, luas permukaan tabung reaksi tersebut adalah :

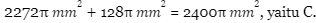
Oke, kalau cuma bahas 1 soal kurang banget ya?! Kita lanjut ke soal berikutnya.

Soal 2

Penyelesaian:

Cek terlebih dahulu, bahwa tenda tersebut terbentuk dari 2 bangun ruang sisi lengkung, yaitu tabung dan kerucut. Nah, karena pertanyaannya adalah volume, jadi kita bisa langsung menghitung volume tendanya. 

Tapi, kalo pertanyaannya adalah luas permukaan, kamu harus analisis lagi bentuk tabung dan kerucutnya, apakah punya tutup dan alas atau tidak.

Diketahui:

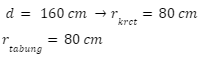
Volume tenda = Volume kerucut + volume tabung

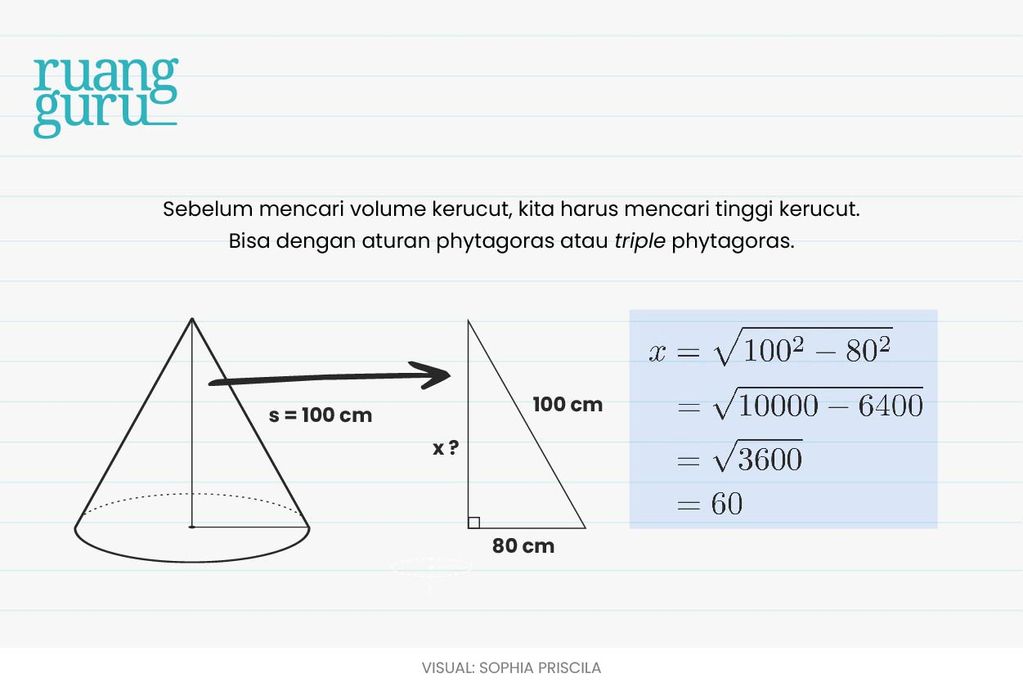
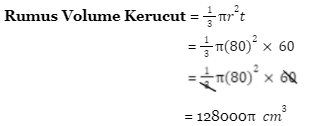
Next, kita cari volume tabung!
Jangan lupa cari tinggi tabung terlebih dahulu.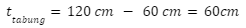

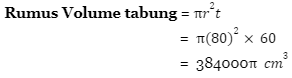
Jadi, volume tenda tersebut adalah

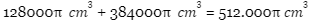
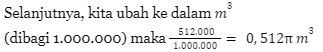
Untuk soal kedua ini, jawaban yang tepat adalah D.

Soal 3

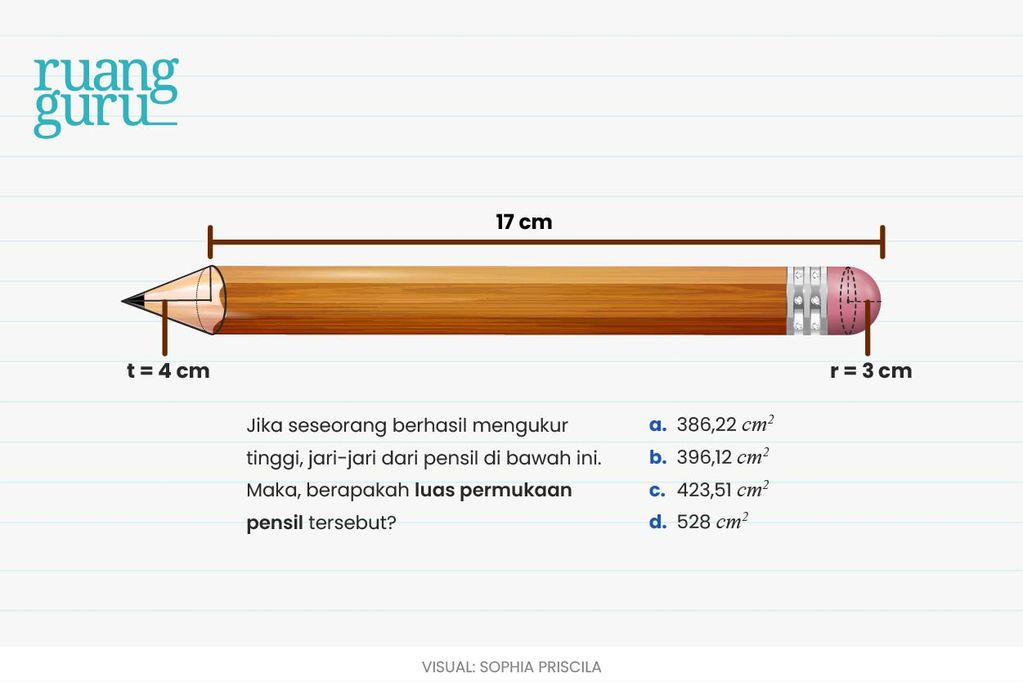
Penyelesaian:

Kalau kamu lihat pensil di atas tersusun dari 3 bangun ruang sisi lengkung, yaitu kerucut, tabung, dan setengah bola. Eits, tapi kita analisis lagi nih, bangun ruang tersebut apakah memiliki tutup/alas? 

Jawabannya enggak ya, guys! Ketiga susunan bangun ruangnya terhubung tanpa adanya tutup dan alas. Makanya, kerucut, tabung, dan bola dalam soal ini yang dihitung adalah selimutnya aja. Yuk, kita hitung!

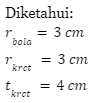
Yang akan kita cari:

Luas permukaan pensil = luas selimut kerucut + luas selimut tabung + luas setengah bola

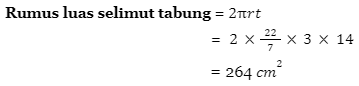
• Cari luas setengah bola tanpa tutup
  
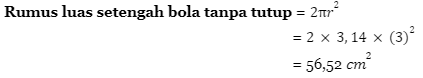
  Nah, karena kita udah dapat masing-masing nilai luasnya, jadi luas permukaannya adalah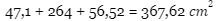

Maka, jawaban yang tepat adalah A.

Soal 4

Sebuah gelas berbentuk tabung memiliki diameter 14 cm dan tinggi 12 cm. Gelas telah terisi teh sebanyak ½ dari total volumenya. Sebongkah batu es berbentuk bola dan berjari-jari 3 cm dimasukkan ke dalam gelas. Berapa tinggi teh dalam gelas setelah batu es dimasukkan ke dalam gelas?

Penyelesaian:

Di soal ini berbeda sama soal sebelumnya ya. Ada 2 bangun ruang yaitu tabung dan bola. 

Diketahui: 

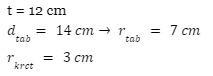
Yang ditanya adalah tinggi teh dalam gelas setelah batu es dimasukkan.

• Kita cari dulu volume teh dalam gelas

Karena dalam kondisi ini gelas yang berbentuk tabung sudah berisi teh setengah bagian.

Maka, rumusnya menjadi ½ volume tabung, atau bisa ditulis seperti ini:

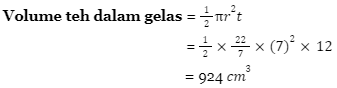
Next, kita cari volume es batu yang berbentuk bola.

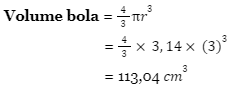
Jadi, tinggi teh di gelas setelah batu es dimasukkan adalah 6,734 cm.

Gimana nih? ternyata seru juga bahas soal gabungan bangun ruang sisi lengkung ini. Hal penting yang harus kamu perhatikan sih bentuk pasti dari bangun yang ada di soal. Jangan sampai salah mengenali struktur bangun ruang sisi lengkungnya ya!

Wah, nggak kerasa nih udah banyak soal yang kita bahas. Tapi, semua soal ini nggak ada artinya kalo kamu nggak lanjut latihan bahas-bahas soal. Supaya kalo dapet soal HOTS, kamu udah santai ngerjainnya.

Ohya, aku juga mau kasih tau nih, kalo ada soal yang belum bisa terpecahkan atau ragu-ragu, langsung aja tanya ke Roboguru. Tinggal foto soalnya, langsung keluar deh jawabannya. Udah gampang, gratis juga loh, mantep kan! 

Sampai jumpa di artikel selanjutnya ya, dadah!

Referensi:

Subchan, dkk. (2018) Matematika SMP/MTs Kelas IX. Jakarta : Pusat Perbukuan, Departemen Pendidikan Nasional.