Perbedaan Kesebangunan dan Kongruen pada Bangun Datar | Matematika Kelas 9

Artikel Matematika kelas 9 ini akan menjelaskan tentang perbedaan kekongruenan dan kesebangunan dalam bangun datar berdasarkan ciri-cirinya. Yuk, belajar bersama!

—

Pernah gak ketika kamu ngerjain tugas kelompok, ada aja anggota kelompok yang malah mainan smartphone. Hayo, siapa yang kayak gini?

Salah satu tips agar fokus mengerjakan tugas adalah dengan mengumpulkan semua smartphone di satu tempat, biar gak ada yang mainin. Kamu pernah kayak gini gak?

Emang ya, mengumpulkan smartphone di satu tempat bisa bikin lebih fokus ngerjain tugas. Pas udah selesai ngerjain dan mau ngambil smartphone, pastikan kalau kamu gak salah ambil ya, siapa tau ada yang tipe smartphonenya sama kayak kamu.

Kalau di dalam matematika, benda yang sama persis ada sebutannya lho, yaitu kongruen. Kalau dalam hubungan, butuh dua hati yang kongruen biar bisa bersatu. Jadi, kalau ngerasa ada yang beda, udah gak kongruen lagi, gak usah dipaksain ya.

Loh, loh, kok malah jadi ngelantur gini sih. Hehehe…

Dalam materi bangun datar, selain mengenal berbagai macam bangun datar, sifat-sifat, hingga rumus mencari luas dan kelilingnya, kamu juga akan mempelajari tentang istilah kongruen dan sebangun. Wah, apa tuh ya? Yuk, kita simak bersama di artikel ini!

Baca Juga: Rumus Bangun Datar (Luas dan Keliling) serta Contohnya

Pengertian Kekongruenan pada Bangun Datar

Sederhananya, kongruen adalah istilah yang digunakan untuk menyatakan dua bangun datar yang sama persis. Baik itu ukurannya, sifatnya, maupun sudut yang dimilikinya.

Nah, kongruen dilambangkan dengan simbol “≡” atau “≅”. Kamu bisa membacanya dengan sebutan “tanda sama dengan garis ganda”. Artinya, dua objek tersebut memiliki kesamaan yang sama persis (kongruen).

Contoh kekongruenan sering kita temui dalam kehidupan kita, loh! Contohnya aja, jendela yang ada di ruang tamu kamu. Pasti punya bentuk yang sama persis. Atau, kalau di sekolah ada temen kamu yang punya smartphone dengan merk dan tipe serupa dengan kamu, itu tandanya HP kamu dan temanmu kongruen!

Baca Juga: Rumus Luas & Volume Kerucut serta Contoh Soalnya

Contoh Kekongruenan

Syarat Kongruen pada Bangun Datar

Dua bangun yang sama persis emang disebut sebagai kongruen. Tapi, secara formal, dalam konteks bangun datar, dua buah bangun datar dapat dikatakan kongruen jika memenuhi dua syarat, yaitu:

• Sudut-sudut yang bersesuaian sama besar
• Sisi-sisi yang bersesuaian sama panjang

Oke, supaya kamu lebih paham, coba perhatikan gambar di bawah ini, deh!

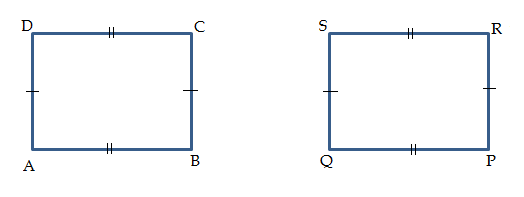
Contoh bangun datar yang kongruen. (Sumber: deni11math.wordpress.com)

Kalau kita bedah berdasarkan sifat-sifatnya, maka:

• Sudut-sudut yang bersesuaian sama besar

Persegi panjang ABCD dan persegi panjang QPRS memiliki sudut-sudut yang sama besar, yaitu ∠A = ∠Q, ∠B = ∠P, ∠C = ∠R, ∠D = ∠S. Sudut-sudut tersebut sama-sama merupakan sudut siku-siku 90°.

• Sisi-sisi yang bersesuaian sama panjang

Kemudian, sisi-sisi yang bersesuaian pada persegi panjang ABCD dan persegi panjang QPRS juga memiliki panjang yang sama. Sisi AB = sisi QP, sisi BC = sisi PR, sisi CD = sisi RS, sisi DA = sisi SQ.

Nah, karena kedua syarat kekongruenan telah terpenuhi, maka dapat dikatakan bahwa persegi panjang ABCD kongruen dengan persegi panjang QPRS (ABCD ≡ QPRS).

Pengertian Kesebangunan pada Bangun Datar

Selain kongruen, ada juga yang disebut dengan sebangun. Kalau kesebangunan adalah istilah yang digunakan untuk menyatakan dua bangun datar yang memiliki proporsi yang mirip satu sama lain.

Mmm, gampangnya sih, kalau kamu menemukan dua bangun datar yang bentuknya sama tapi ukurannya berbeda, maka dua bangun datar tersebut dapat dikatakan sebangun.

Kesebangunan disimbolkan dengan “≈” yang dibaca sebagai “sebangun dengan”.

Baca Juga: Rumus Luas dan Volume Bola, Cara Menghitung & Contohnya

Contoh Kesebangunan

Contoh sebangun tuh gini, kamu tahu gak berapa luas negara Indonesia?

Wilayah Indonesia terbentang sepanjang 3.977 mil di antara Samudra Hindia dan Samudra Pasifik. Luas daratannya 1.922.570 km² dan luas perairannya 3.257.483 km². Dengan ukuran seluas itu, gak mungkin ya bisa menggambar Indonesia di atas selembar kertas dengan ukuran sesungguhnya.

Agar bisa menggambar peta Indonesia, digunakanlah skala. Nah, kalau misalkan petanya memakai skala 1:1.000.000 berarti 1 cm di peta sama dengan 1.000.000 cm pada aslinya. Karena skala merupakan perbandingan, maka peta juga termasuk contoh kesebangunan.

Selain peta, ada apalagi ya yang sebangun?

Syarat Kesebangunan pada Bangun Datar

Kalau kita bicara dalam konteks bangun datar, selain perbandingan panjang yang sama, agar bisa disebut sebangun, dua bangun datar harus memenuhi syarat:

• Sudut-sudut yang bersesuaian sama besar
• Sisi-sisi yang bersesuaian memiliki perbandingan yang sama

Yuk, kita perhatikan gambar di bawah biar kamu nggak bingung!

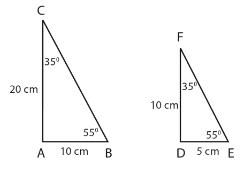
Contoh bangun datar yang sebangun. (Sumber: kompas.com)

Kita bedah satu per satu, ya.

• Sudut-sudut yang bersesuaian sama besar

Sama seperti syarat dua bangun yang kongruen, pada bangun datar yang sebangun juga harus memiliki besar sudut yang sama. Nah, pada segitiga ABC dan DEF, keduanya juga memiliki sudut-sudut yang sama besar, loh. Besar ∠A = ∠D = 90°, ∠B = ∠E = 55°, dan ∠C = ∠F = 35°.

• Sisi-sisi yang bersesuaian memiliki perbandingan yang sama

Selain itu, sisi-sisi yang bersesuaian antara segitiga ABC dengan segitiga DEF juga memiliki perbandingan yang sama.

• Sisi AB dan sisi DE memiliki perbandingan 10 : 5 = 1 : 2
• Sisi CA dan sisi FD memiliki perbandingan 20 : 10 = 1 : 2

Karena kedua syarat kesebangunan telah terbukti, maka bisa dikatakan kalau segitiga ABC sebangun dengan segitiga DEF (ABC ≈ DEF).

Apa Bedanya Kesebangunan dan Kongruen?

Gimana nih sampai sini, apakah kamu sudah bisa membedakan antara benda yang sebangun dan kongruen?

Hal mendasar yang membedakan kongruen dan sebangun adalah, kalau kongruen sisi-sisi yang bersesuaian harus sama panjang, sedangkan kalau sebangun perbandingan sisi-sisi yang bersesuaian harus sama besar. Jadi, semua bangun yang kongruen udah pasti sebangun, tapi kalau sebangun belum tentu kongruen ya.

Baca Juga: Macam-Macam Transformasi Geometri, Sifat & Contoh Soal

Contoh Soal Kesebangunan dan Kekongruenan

1. Pada ∠ABC, diketahui AC ≡ DE. Bila panjang BE = x cm, maka nilai x adalah …

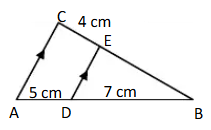
Pembahasan:

Diketahui:

AD = 5 cm

DB = 7 cm

AB = 5 cm + 7 cm = 12 cm

CE = 4 cm

AC ≡ DE

Ditanya: BE … ?

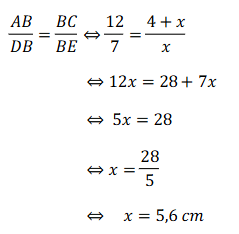
Jadi, diketahui nilai x = 5,6 cm.

2. Perhatikan gambar berikut!

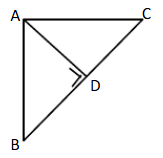
Jika panjang AB = 12 cm dan BC = 15 cm, maka panjang AD adalah …

Pembahasan:

Diketahui:

AB = 12 cm

BC = 15 cm

Ditanya: AD … ?

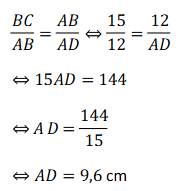
Jadi, panjang AD adalah 9,6 cm.

—

Sekarang kamu udah paham kan bedanya kongruen dan sebangun? Kalau kamu masih ada pertanyaan seputar materi kesebangunan dan kongruen atau materi lainnya, bisa lho langsung tonton videonya di ruangbelajar biar belajar kamu makin seru!