Kejadian Majemuk dalam Teori Peluang Matematika | Matematika Kelas 12

RG Squad, jika kamu diminta Ibu untuk merapikan bola warna-warni yang kalian miliki ke dalam kotak mainan. Namun tiba-tiba, adikmu yang masih kecil minta diambilkan bola. Secara acak, kamu akan mengambil kembali bola tersebut. Nah, peluang terambilnya bola warna biru dan merah kira-kira ada berapa ya RG Squad? Kejadian-kejadian seperti ini dapat dijawab dengan mempelajari materi kejadian majemuk di dalam teori peluang matematika. Simak caranya di bawah ini!

Apabila ada kejadian atau percobaan yang terjadi lebih dari satu kali sehingga menghasilkan kejadian baru, maka kejadian baru itu disebut kejadian majemuk. Terdapat beberapa kejadian yang disebut sebagai kejadian majemuk. Yuk kita pelajari lebih lanjut!

1. Dua Kejadian Sembarang

Untuk dua kejadian sembarang A dan B pada ruang sampel S, berlaku rumus:

P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

Contoh :

Dari 45 siswa pada suatu kelas, diketahui 28 siswa suka Matematika, 22 siswa suka bahasa Inggris, dan 10 siswa suka kedua-duanya. Jika seorang siswa dipilih secara acak, tentukan peluang siswa yang terpilih adalah yang menyukai Matematika atau bahasa Inggris!

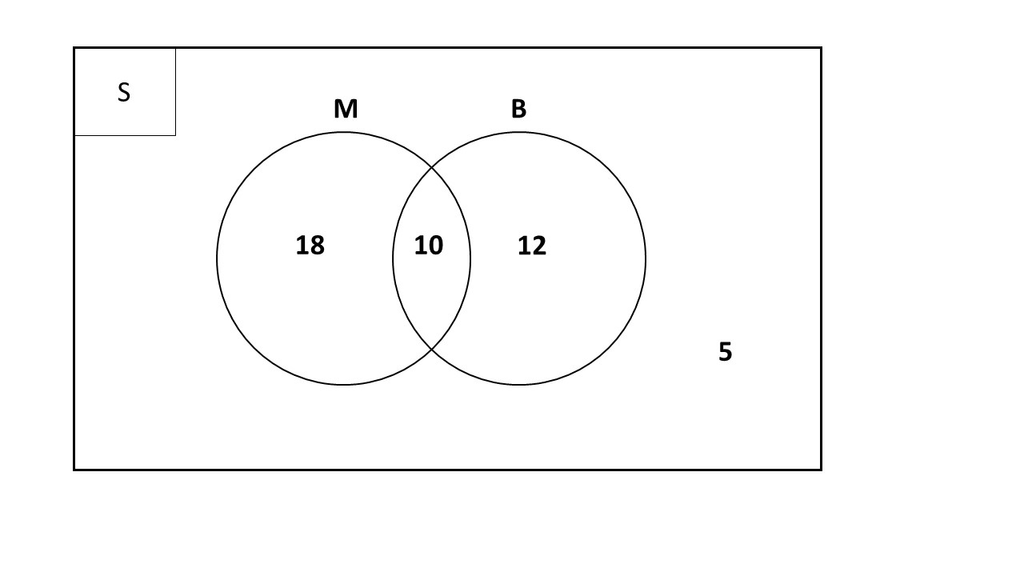
n(S) = 45

Suka Matematika, n(M) = 28

Suka Bahasa Inggris, n(B) = 22

Suka keduanya, n(M ∩ B ) = 10

Jawab :

n(S) = 45

Suka Matematika, n(M) = 28

Suka Bahasa Inggris, n(B) = 22

Suka keduanya, n(M ∩ B ) = 10

Peluang terpilih yang suka Matematika atau Bahasa Inggris ialah:

P (M ∪ B) = P (M) + P (B) – P (M ∩ B)

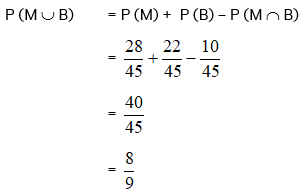
2. Komplemen Suatu Kejadian

Rumus: P (A^c) = 1 – P (A)

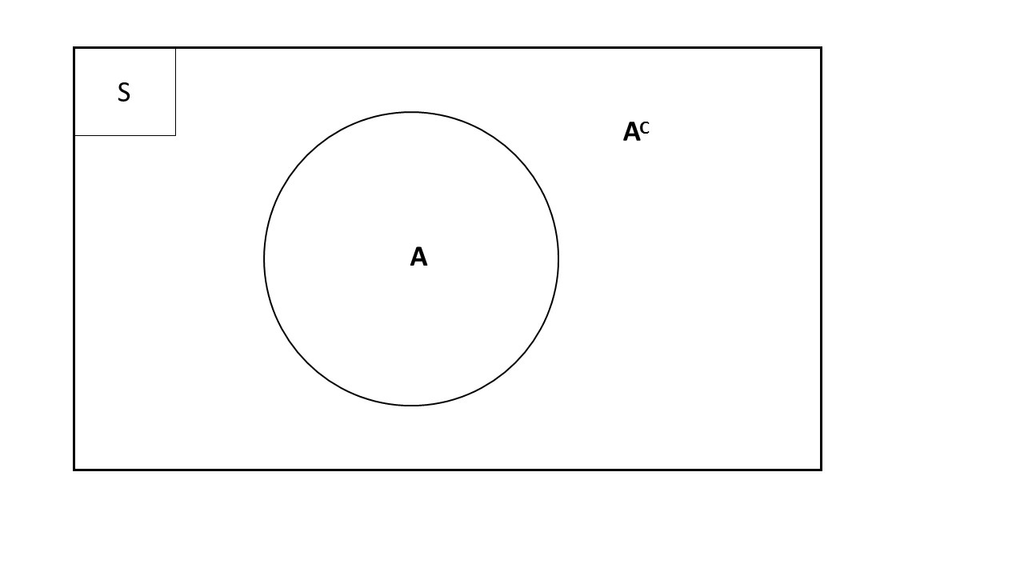Contoh:

Sebuah dadu dilempar sekali, tentukan peluang munculnya mata dadu lebih dari dua.

Jawab:

Sebuah dadu dilempar sekali, maka n (S) = 6

Jika A = {mata dadu lebih dari sama dengan 2}

Sehingga A^c = { mata dadu kurang dari atau sama dengan 2 } = {1, 2}, n(A^c) = 2

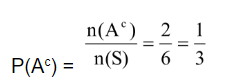
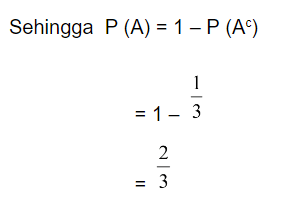
Jadi, peluang munculnya mata dadu lebih dari 2 adalah 2/3

3. Dua Kejadian Saling Lepas

Rumus: P (A ∪ B) = P(A) + P (B)

Contoh:

Pada pelemparan sebuah dadu bermata 6, berapakah peluang mendapatkan dadu mata 1 atau 3 ?

Jawab:

A = {1}, B = {3}

n(A) = 1, n(B) = 1

Peluang mendapatkan dadu mata 1 atau 3:

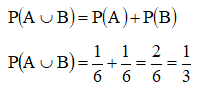
RG Squad, pembahasan tentang teori peluang ini masih ada di peluang kejadian majemuk bagian ke dua lho. Kalau kalian masih bingung dengan penjelasan di atas, kalian bisa tonton video belajarnya hanya di ruangbelajar!

Sumber Referensi 

Waluyo S, Sutrisna. () Konsep dan Penerapan Matematika SMA/MA/SMK/MAK. Jakarta:Bailmu

Artikel diperbarui 25 Januari 2021