Teori Peluang Kejadian Majemuk (bagian 2) | Matematika Kelas 12

RG Squad, sebelumnya kalian telah belajar teori peluang kejadian majemuk bagian 1 mengenai dua kejadian sembarang, komplemen suatu kejadian, dan dua kejadian saling lepas. Nah, di artikel kali ini akan melanjutkan pembahasan tersebut dengan penambahan penjelasan tentang dua kejadian saling bebas dan dua kejadian bersyarat.
1. Dua Kejadian Saling Bebas
Kejadian A dan B dikatakan saling bebas jika kejadian A tidak mempengaruhi kejadian B dan kejadian B tidak mempengaruhi kejadian A. Dirumuskan:
P (A ∩ B) = P (A) X P (B)
Contoh:
Jika peluang Andi dapat menyelesaikan suatu soal adalah 0,4 dan peluang Budi dapat menyelesaikan soal yang sama adalah 0,3 maka peluang mereka berdua dapat menyelesaikan soal tersebut adalah …
Jawab :
P(A) = 0,4
P(B) = 0,3
Peluang Andi dan Budi dapat menyelesaikan soal:
- Dua Kejadian Bersyarat
Jika kejadian A dan B tidak saling bebas, kejadian B dipengaruhi oleh kejadian A atau kejadian B dengan syarat A, dirumuskan:
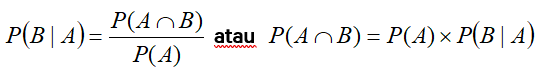
Contoh:
Sebuah dadu dilempar sekali. Tentukan peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima lebih dahulu.
Jawab:
S = {1, 2, 3, 4, 5, 6}, n(S) = 6
A = Kejadian munculnya angka prima
A = {2, 3, 5}, n(A) = 3
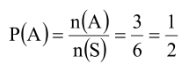
B = Kejadian muncul mata dadu ganjil
B = {1, 3, 5}
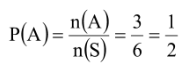
Peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima lebih dahulu:
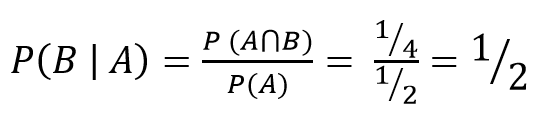
Setelah mempelajari seluruh peluang kejadian majemuk, maka dapat disimpulkan:
Kali ini RG Squad telah selesai belajar tentang teori peluang, yaitu mengenai aturan perkalian dan faktorial, permutasi, kombinasi dan Binomial Newton, percobaan ruang sampel dan peluang suatu kejadian, dan peluang kejadian majemuk.
Yuk belajar berbagai topik dan pelajaran lainnya di ruangbelajar!
Sumber Referensi
Sharma S. N, Widiastuti N, Himawan C, dkk (2017) Jelajah Matematika SMA Kelas XII Program Wajib. Jakarta:Yudisthira
Artikel diperbarui 21 Januari 2021













