Latihan Soal Tryout UTBK 1 Tahun 2021: Matematika IPA

Ayo, persiapkan dirimu sejak dini dalam menghadapi UTBK 2021! Lihat latihan soal tryout UTBK Episode 1 tahun 2021 untuk mata pelajaran Matematika IPA.

—

Sudah mengikuti tyout UTBK 1 dari ruanguji? Nah, masih penasaran mengenai pembahasan soal-soalnya? Yuk, lihat latihan soal tryout UTBK Episode 1 tahun 2021 untuk mata pelajaran Matematika IPA berikut ini. Jangan lupa untuk mempelajari lagi materi yang belum kamu kuasai ya.

1. Suatu perusahaan memproduksi x unit barang dengan biaya 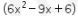ribu rupiah untuk tiap unit. Jika barang tersebut terjual habis dengan harga Rp42.000,00 untuk tiap unit, maka keuntungan maksimum yang diperoleh perusahaan tersebut adalah ….

1. Rp24.000,00
2. Rp60.000,00
3. Rp84.000,00
4. Rp96.000,00
5. Rp156.000,00

 

Pembahasan: 

Misalkan f(x) menyatakan total biaya produksi x unit barang, g (x) menyatakan harga jual x unit barang dalam satuan ribu rupiah, dan h(x) menyatakan kentungan yang diperoleh atas penjualan x unit barang, maka diperoleh hasil-hasil sebagai berikut.

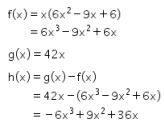
Agar maksimum, nilai turunan pertama h(x) harus bernilai 0. Maka

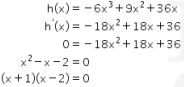
Diperoleh x = -1 atau x = 2. Karena x menyatakan jumlah barang dan nilainya tidak mungkin negatif atau pecahan, sehingga x yang diambil adalah x = 2.

Dilakukan substitusi x = 2 ke h(x), didapat

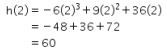
Maka keuntungan maksimum yang diperoleh perusahaan tersebut adalah Rp60.000,00.

Jadi, jawabannya adalah B.

2. Sebuah balok ABCD.EFGH memiliki panjang rusuk AB = 6 dan BC = CG = 4. Jika titik P terletak di tengah rusuk AB dan θ adalah sudut antara EP dan PG, maka nilai cosθ adalah ….

 

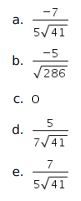
Pembahasan: 

Perhatikan gambar berikut ini!

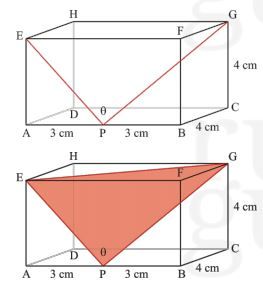
Perhatikan bahwa

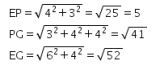
Sehingga

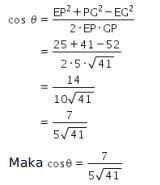
Jadi, jawabannya adalah E.

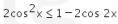3. Himpunan bilangan real x pada selang yang memenuhi  memiliki bentuk  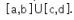Nilai dari 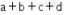adalah ….

 

 

Pembahasan: 

Perhatikan bahwa

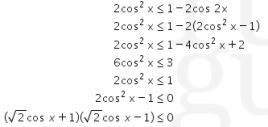
Pembuat nolnya adalah

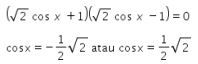
Maka didapat nilai-nilai x yang memenuhi adalah

Didapat garis bilangannya sebagai berikut.

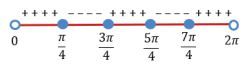
Karena tanda pertidaksamaannya adalah maka didapat solusinya adalah 

Sehingga intervalnya adalah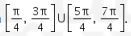

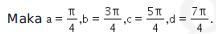
Akibatnya,

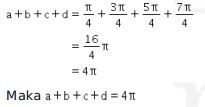
Jadi, jawabannya adalahA.

4. Diketahui sebuah segitiga ABC dengan sudut B adalah 105⁰ dan sudut A adalah 15⁰. Jika panjang AC adalah 5, maka panjang BC adalah ….

 

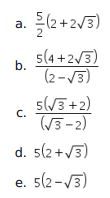
Pembahasan: 

Perhatikan gambar berikut ini!

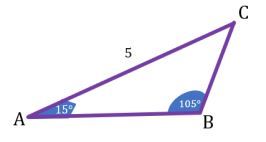
Dari gambar tersebut, didapat

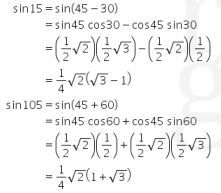
Dengan menggunakan aturan sinus,

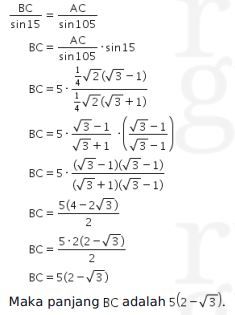
Jadi, jawabannya adalah E.

5. Diketahui vektor-vektor 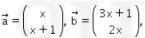 dan . Jika 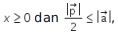 maka interval x yang memenuhi adalah ….

 

Pembahasan: 

Dari soal diketahui bahw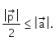a  Maka

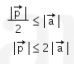
Kemudian, karena , maka 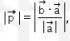 sehingga

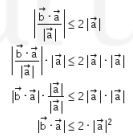
Lalu perhatikan bahwa

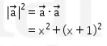
dan juga

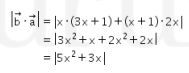
Karena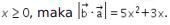 

Sehingga didapat

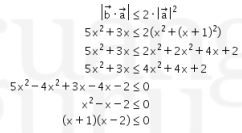
Pembuat nol dari bentuk di ruas kiri adalah

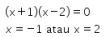
Didapat garis bilangan sebagai berikut.

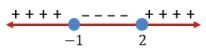
Karena tanda pertidaksamaannya adalah  maka solusinya adalah 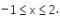 Namun, karena pada soal
diketahui  maka diambil irisannya, yaitu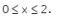 

Sehingga, interval x yang memenuhi adalah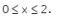

Jadi, jawabannya adalah B.

6. 

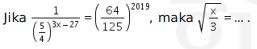
1. 25
2. 26
3. 27
4. 576
5. 676

 

Pembahasan: 

Dengan menggunakan sifat-sifat pada eksponen, diperoleh

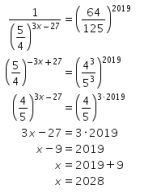
sehingga

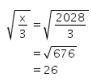
Dengan demikian, kita peroleh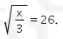 

Jadi, jawaban yang tepat adalah B.

7. Diketahui sistem persamaan

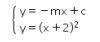
Jika sistem persamaan tersebut memiliki tepat satu penyelesaian, maka jumlah semua nilai m yang
mungkin adalah ….

1. – 32
2. – 20
3. – 16
4. – 8
5. – 4

 

Pembahasan: 

Penyelesaian sistem persamaan pada soal dapat diselesaikan sebagai berikut.

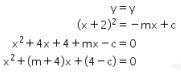
Karena sistem persamaan di atas meiliki tepat satu penyelesaian, maka nilai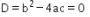 

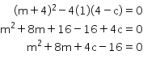
Sehingga

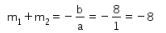
Maka jumlah semua nilai m adalah -8.

Jadi, jawaban yang tepat adalah D.

8. 

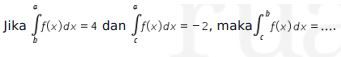
1. – 2
2. – 6
3. 0
4. 2
5. 6

 

Pembahasan:

Ingat kembali beberapa sifat yang berlaku pada integral, yaitu

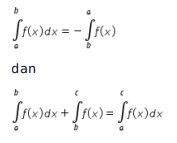
Dengan menggunakan kedua sifat tersebut, diperoleh

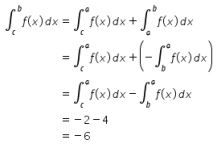
Dengan demikian,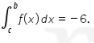 

Jadi, jawaban yang tepat adalah B.

9. 

 

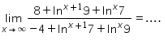
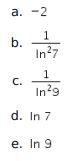
Pembahasan:

Perhatikan bahwa

Dengan demikian,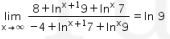 

Jadi, jawaban yang tepat adalah E.

10. Jika 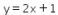digeser sejauh a satuan ke kanan dan sejauh b satuan ke bawah, kemudian dicerminkan terhadap sumbu-y , bayangannya menjadi 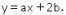Nilai dari 3ab adalah ….

1. – 15
2. – 12
3. – 10
4. – 6
5. 0

 

Pembahasan:

Garis 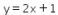digeser sejauh a satuan ke kanan dan sejauh b satuan ke bawah, maka

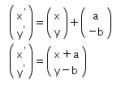
sehingga 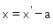 dan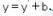 

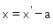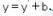Dengan substitusi dan ke 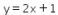, maka bayangan garis 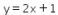hasil pergeseran di
atas adalah

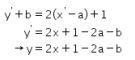
Kemudian garis tersebut dicerminkan terhadap sumbu-y, maka

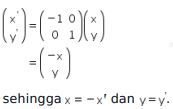
Dengan substitusi ke 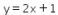, maka hasil pencerminan garis 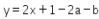terhadap sumbu-y adalah

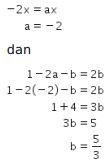
Dengan demikian, kita peroleh

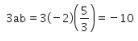
Jadi, jawaban yang tepat adalah C. 

11. Diketahui sistem persamaan berikut.

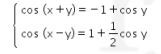
Jika 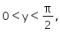 maka nilai dari adalah ….

 

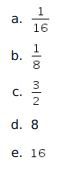
Pembahasan:

Kita tuliskan dua persamaan yang ada pada soal, yaitu sebagai berikut.

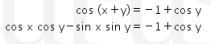
dan

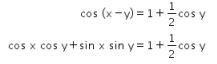
Eliminasi 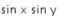dengan cara berikut.

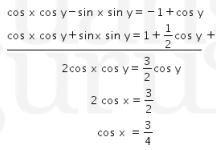
Oleh karena itu, didapat nilai sebagai berikut.

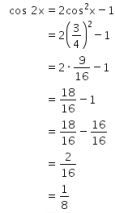
Dengan demikian, nilai dari adalah sebagai berikut.

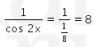
Jadi, jawaban yang tepat adalah D. 

12. Sebuah lingkaran memiliki pusat (p, q) dengan jari-jari 12, dan menyinggung garis 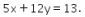 Nilai
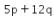yang mungkin adalah ….

 

Pembahasan:

Diketahui bahwa suatu lingkaran memiliki pusat (p, q), jari-jari 12, dan menyinggung garis 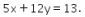. Oleh karena itu, didapat  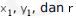sebagai berikut.

Kemudian, garis 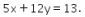dapat dituliskan sebagai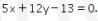 

Didapat nilai a, b, dan c sebagai berikut.

a = 5

b = 12

c = – 13

Selanjutnya, dapat diperhatikan perhitungan di bawah ini.

Terdapat dua kemungkinan yaitu 

Kemungkinan pertama:

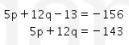Kemungkinan kedua:

Dengan demikian, nilai 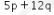 yang mungkin adalah -143 dan 169.

Jadi, jawaban yang tepat adalah D.

13. Suku banyak 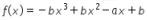 habis dibagi  dan dibagi  bersisa 20. Nilai ab adalah ….

1. – 16
2. – 4
3. 4
4. 8
5. 16

 

Pembahasan:

Dapat diperhatikan pembagian polinomial berikut ini.

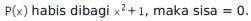Oleh karena itu, didapat persamaan berikut.

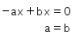
Kemudian, diketahui bahwa 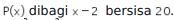 Oleh karena itu, substitusi  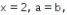dan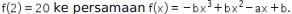 

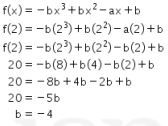
Dikarenakan .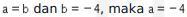

Akibatnya, diperoleh nilai ab sebagai berikut.

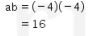
Dengan demikian, nilai ab = 16.

Jadi, jawaban yang tepat adalah E.

14. Seorang berkendara dengan kecepatan 100 km/jam selama satu jam pertama. Pada jam kedua, kecepatan berkurang menjadi seperlimanya. Demikian juga pada jam berikutnya. Jarak terjauh yang dapat ditempuh orang tersebut adalah … km.

1. 150
2. 125
3. 100
4. 75
5. 50

 

Pembahasan:

Dapat diperhatikan bahwa jarak yang ditempuh oleh seseorang pada jam pertama adalah 100 km. Kemudian, diketahui bahwa kecepatannya berkurang  pada jam kedua. Akibatnya, jarak yang ditempuh orang tersebut pada jam kedua adalah Begitupun seterusnya sehingga jarak yang ditempuh orang tersebut dapat dituliskan sebagai berikut.

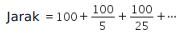
Jarak yang ditempuh oleh seseorang tersebut membentuk deret geometri tak hingga dengan a = 100 dan r = sehingga dapat dituliskan sebagai berikut.

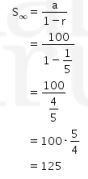
Oleh karena itu, jarak terjauh yang dapat ditempuh orang tersebut adalah 125 km.

Jadi, jawaban yang tepat adalah B.

15. Garis 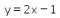dirotasi searah jarum jam sebesar 180⁰ terhadap titik asal. Kemudian, digeser ke bawah sejauh b satuan dan ke kiri sejauh a satuan sehingga bayangannya menjadi 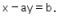. Nilai adalah ….

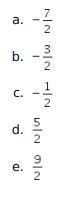
Pembahasan:

Ingat bahwa jika suatu benda dirotasi sebesar searah jarum jam, maka sudut rotasinya diberi tanda negatif, sehingga menjadi

Diketahui bahwa garis 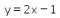dirotasi sebesar 180⁰ searah jarum jam terhadap titik asal, maka bayangannya adalah sebagai berikut.

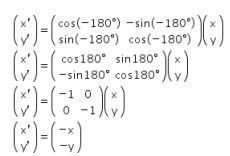
Oleh karena itu, didapat nilai x dan y sebagai berikut.

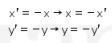
Akibatnya, garis 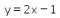menjadi

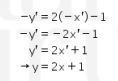
Kemudian, digeser ke bawah sejauh b satuan dan ke kiri sejauh a satuan atau dapat dituliskan sebagai

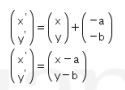
Didapat nilai x dan y berikut ini

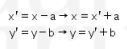
Akibatnya, garis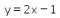 menjadi

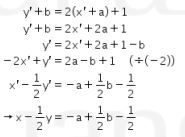
Diketahui pada soal bahwa  sama dengan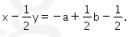 

Didapat

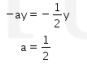
dan

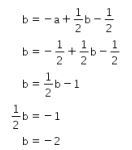
Oleh karena itu, nilai dapat dihitung dengan cara sebagai berikut

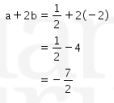
Dengan demikian, nilai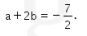

Jadi, jawaban yang tepat adalah A.

16. 

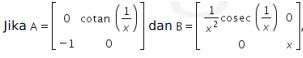
maka nilai dari 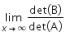 adalah ….

 

Pembahasan:

Diketahui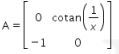 

maka didapat

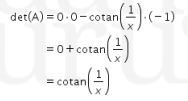
Selanjutnya diketahui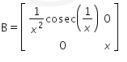 

maka didapat

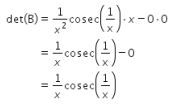
Sehingga didapat

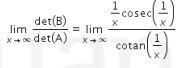
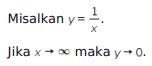
Oleh karena itu didapat

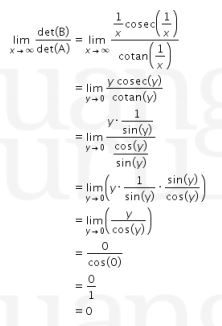
Dengan demikian, nilai dari 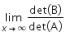adalah 0.

Jadi, jawaban yang tepat adalah C.

17. Misalkan fungsi f memenuhi 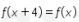 untuk setiap  Jika  maka nilai dari 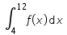 adalah ….

1. – 3
2. 3
3. – 5
4. 6
5. – 6

 

Pembahasan:

Ingat bahwa

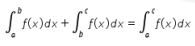
Jika f periodik dengan periode p, maka

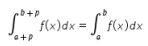
Suatu fungsi f adalah periodik jika terdapat suatu bilangan p sedemikian sehingga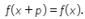 

Karena 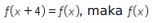periodik dengan periode 4.

Sehingga berlaku

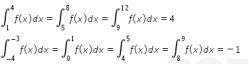
Dengan menggunakan sifat integral di atas, maka

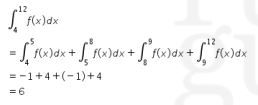
Dengan demikian, nilai dari 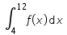adalah 6.

Jadi, jawaban yang tepat adalah D.

18. Dari angka-angka 1, 4, 5, 6, 8, 9 akan dibentuk bilangan genap yang terdiri dari 3 digit berbeda. Banyak bilangan yang terbentuk yang nilainya kurang dari 400 adalah ….

1. 30
2. 20
3. 12
4. 9
5. 8

 

Pembahasan:

Diketahui angka-angka 1, 4, 5, 6, 8, 9.

Misalkan bilangan yang akan dibentuk adalah a₁a₂a_3.

a₁ adalah angka yang menempati ratusan, a₂ adalah angka yang menempati puluhan, dan a₃ adalah angka yang menempati satuan.

Karena akan dibentuk bilangan genap, maka banyak angka yang menempati satuan (yaitu a₃) ada 3 (angka 4, 6, 8)

Kemudian bilangan yang dibentuk nilainya kurang dari 400, maka banyak angka yang menempati ratusan (yaitu a₁) ada 1 (angka 1)

Selanjutnya perhatikan bahwa bilangan terdiri dari 3 digit berbeda, maka banyak angka yang menempati puluhan (yaitu a₂) ada 4 (angka yang tersisa)

Sehingga didapat

Dengan demikian, banyak bilangan yang terbentuk yang nilainya kurang dari 400 adalah 12.

Jadi, jawaban yang tepat adalah C. 

19. Diketahui barisan aritmetika dengan U_k menyatakan suku ke-k. Jika U_{k+2 =} U₂ + kU₁₇ – 3, maka U₁+U₁₃ +U₁₉+U₃₅= ….

 

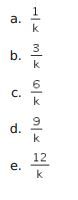
Pembahasan:

Perhatikan bahwa

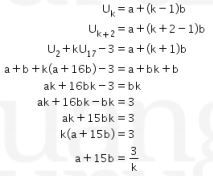
Sehingga didapatkan

Dengan demikian,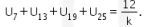

Jadi, jawaban yang tepat adalah E.

20. Suku banyak 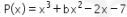 dibagi  bersisa 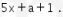 Nilai dari  adalah ….

1. 32
2. 48
3. – 26
4. – 48
5. – 52

 

Pembahasan:

Perhatikan bahwa

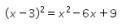
Selanjutnya perhatikan pembagian berikut ini.

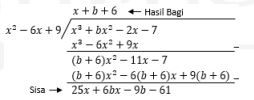
Diketahui 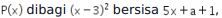maka

Sehingga didapatkan

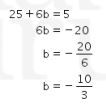
dan

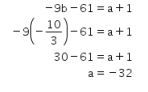
Dengan demikian,

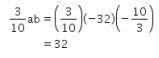
Jadi, jawaban yang tepat adalah A.

UTBK memang masih akan dilaksanakan tahun depan, tapi nggak ada salahnya untuk kamu mencuri start dan mulai mempersiapkan diri sejak dini. Mau mengukur kemampuanmu dalam mengerjakan soal-soal UTBK? Tunggu tryout UTBK Episode 2 dari ruanguji!