Memahami Fungsi Trigonometri Sederhana | Matematika Kelas 10

Belajar fungsi trigonometri sederhana, yuk! Ada fungsi sinus, fungsi cosinus, dan fungsi tangen. Simak pembahasan beserta gambar grafiknya di artikel ini!

—

Pada materi sebelumnya, kamu sudah mempelajari tentang trigonometri secara umum. Nah, kali ini, kamu akan mempelajari materi lanjutannya, yaitu fungsi trigonometri. Apa yang dimaksud dengan fungsi trigonometri?

Fungsi trigonometri adalah suatu fungsi yang grafiknya berulang secara terus menerus dalam periode tertentu. Seperti terlihat pada header di artikel ini, grafik fungsi trigonometri terdiri atas bukit dan lembah yang berulang-ulang secara terus menerus dalam periode tertentu. Oh iya, gambar grafik yang ada di header itu adalah gambar grafik fungsi sinus, ya! Nanti akan kita bahas lebih lanjut di artikel kok, tenang aja, hehe..

Unsur-Unsur Grafik Fungsi Trigonometri

Pada fungsi trigonometri terdapat beberapa unsur, yakni periode, amplitudo, nilai maksimum, dan nilai minimum. Kita bahas satu per satu, ya.

a. Periode

Periode adalah jarak antara dua puncak atau dua lembah pada grafik fungsi trigonometri. Atau dapat diartikan juga sebagai jarak terjadinya grafik fungsi trigonometri tersebut berulang.

b. Amplitudo

Amplitudo adalah setengah dari selisih nilai maksimum dan minimum dari suatu fungsi. Rumus amplitudo yakni sebagai berikut:

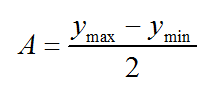
c. Nilai Maksimum

Nilai maksimum adalah nilai tertinggi yang bisa dicapai oleh suatu fungsi trigonometri. Pada grafik, nilai maksimum merupakan titik puncak dari bukit. 

d. Nilai Minimum

Nilai minimum adalah nilai terendah yang bisa dicapai oleh suatu fungsi trigonometri. Pada grafik, nilai minimum merupakan titik terendah dari lembah.

Baca juga: Persamaan Trigonometri Sederhana

Jenis-Jenis Grafik Fungsi Trigonometri

Fungsi trigonometri sederhana terdiri dari tiga macam atau jenis, yaitu fungsi sinus, fungsi cosinus, dan fungsi tangen. Nah, masing-masing fungsi tersebut dapat dijelaskan menggunakan grafik baku fungsi trigonometri. Kita bahas satu per satu, ya!

a. Grafik Fungsi Sinus (y = sin x)

Nilai dari sinus adalah -1 ≤ sin(x) ≤ 1. Untuk gambar grafik fungsi sinus dapat kamu lihat pada infografik berikut.

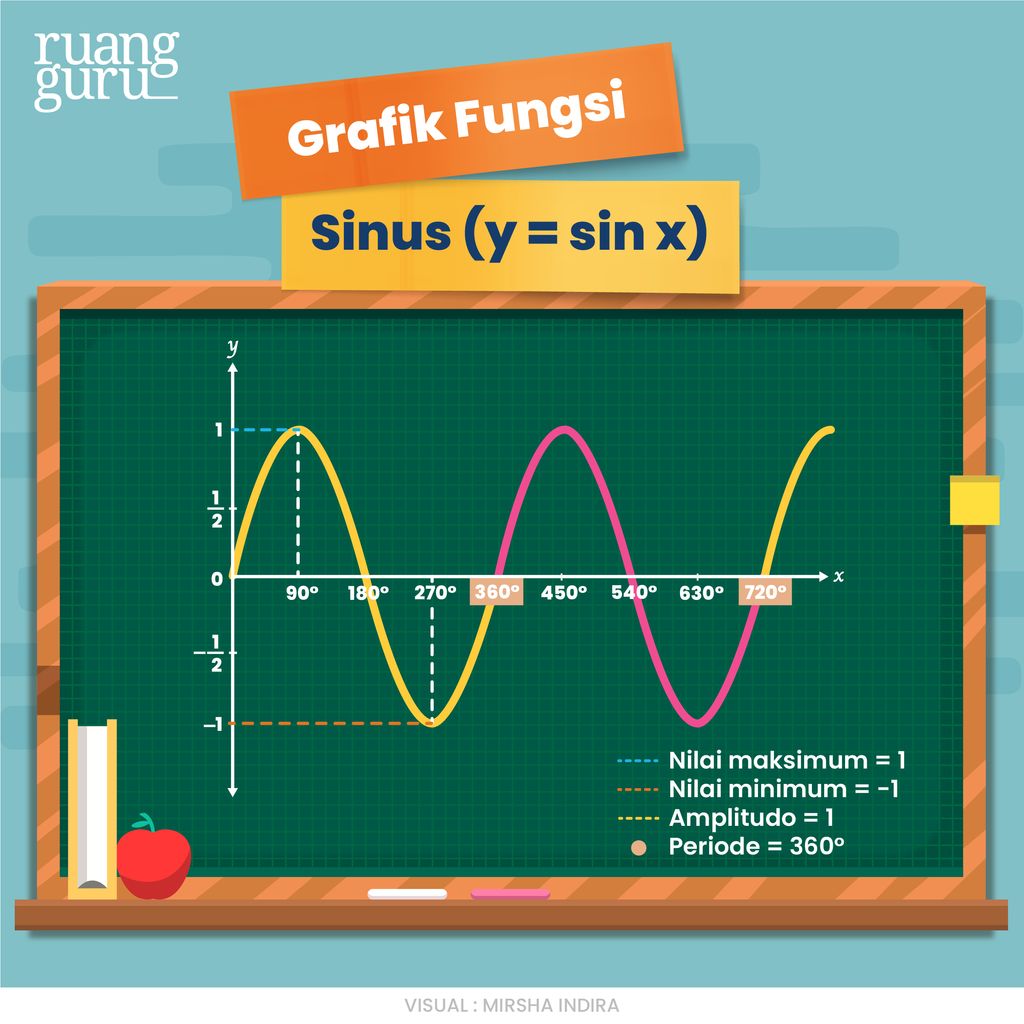
Pada grafik fungsi sinus berlaku:

• Nilai maksimum = 1
• Nilai minimum = -1
• Amplitudo = 1
• Periode = 360°

b. Grafik Fungsi Cosinus (y = cos x)

Nilai dari cosinus adalah -1 ≤ cos(x) ≤ 1. Untuk gambar grafik fungsi cosinus dapat kamu lihat pada infografik berikut.

Pada grafik fungsi cosinus berlaku:

• Nilai maksimum = 1
• Nilai minimum = -1
• Amplitudo = 1
• Periode = 360°

Baca juga: Belajar Fungsi Komposisi & Contohnya, Lengkap!

c. Grafik Fungsi Tangen (y = tan x)

Grafik tangen tidak mempunyai nilai maksimum. Untuk gambar grafik fungsi tangen dapat kamu lihat pada infografik berikut.

Pada grafik fungsi tangen berlaku:

• Nilai maksimum = Tidak ada
• Nilai minimum = Tidak ada
• Amplitudo = Tidak ada
• Periode = 180°

Selain itu, terdapat pula grafik tidak baku pada fungsi trigonometri yang lebih kompleks. Grafik tidak baku ini digambar berdasarkan fungsi seperti tertera dalam tabel berikut.

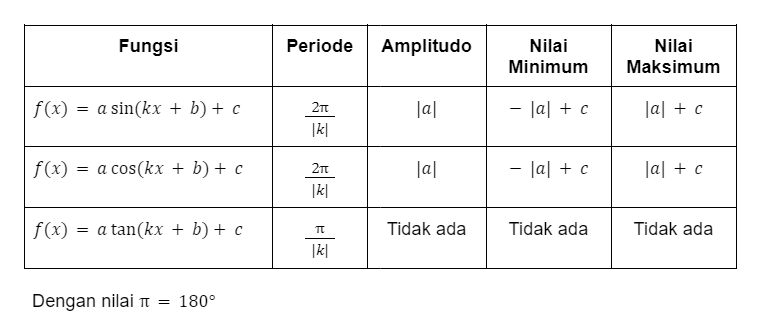
Untuk contoh gambar grafik fungsi trigonometri tidak baku akan dibahas pada materi selanjutnya, ya. Stay tuned terus di ruangbaca, okeyy!

Baca juga: Cara Menyusun Persamaan dari Grafik Fungsi Kuadrat

Nah, sekarang kita coba kerjakan contoh soal di bawah ini aja, ya!

Contoh Soal Fungsi Trigonometri

1. Tentukan nilai maksimum dan nilai minimum dari fungsi trigonometri di bawah in!

a. f(x) = 2 sin 2x + 5

b. f(x) = -3 cos (3(x+90°)) – 8

Penyelesaian:

a. f(x) = 2 sin 2x + 5 → a = 2 , c = 5

Nilai maksimum = |a| + c = |2| + 5 = 7

Nilai minimum = -|a| + c = -|2| + 5 = 3

b. f(x) = -3 cos (3(x+90°)) – 8

     f(x) = – 3 cos (3x+270°) – 8 → a = -3 , c = -8

Nilai maksimum = |a| + c = |-3| + (-8) = 3 – 8 = -5

Nilai minimum = -|a| + c = -|-3| + (-8) = -3 – 8 = -11

—

Begitulah materi kita kali ini tentang fungsi trigonometri sederhana, yang terdiri atas fungsi sinus, fungsi cosinus, dan fungsi tangen. Semoga kamu paham ya, dengan penjelasan di atas. Eits, kamu juga bisa mempelajari lagi materi ini melalui ruangbelajar, lho! Yuk, download sekarang!

Referensi:

Sinaga, B., dkk. (2017). Matematika. Jakarta: Kemendikbud.

Artikel ini pertama kali ditulis oleh Karina Dwi Adistiana dan telah diperbarui oleh Kenya Swawikanti pada 21 April 2022.