Latihan Soal dan Pembahasan UTBK 2021: Matematika Saintek

Masih belum yakin mengerjakan soal UTBK Matematika? Nggak masalah, kamu hanya perlu berlatih lebih giat. Latihan lagi yuk, simak soal Matematika beserta pembahasannya di bawah ini!
—

1) Topik : Aljabar Saintek
Subtopik : Barisan dan Deret
Misal ![]() adalah barisan aritmetika dengan suku pertama a dan beda 2a. Jika
adalah barisan aritmetika dengan suku pertama a dan beda 2a. Jika 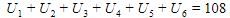 maka nilai dari
maka nilai dari 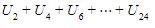 adalah..
adalah..
- 216
- 864
- 900
- 1.632
- 1.776
Jawaban: C
Pembahasan:
Dari soal, diketahui 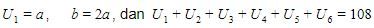
Akan dicari nilai dari 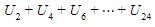
Dapat diperhatikan perhitungan berikut ini.
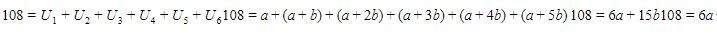
Diperoleh a=3 sehingga b=2a=6. Oleh karena itu, kita dapat menghitung nilai 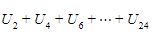 sebagai berikut.
sebagai berikut.
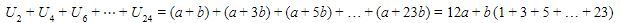
Dapat diperhatikan bahwa 1+3+5++23 adalah deret aritmetika dengan suku pertama 1, beda 3, dan banyaknya suku adalah 12. Akibatnya,
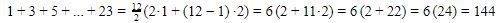
Oleh karena itu, didapat nilai 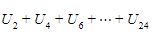 sebagai berikut.
sebagai berikut.
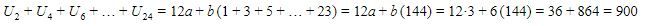
Dengan demikian, nilai dari 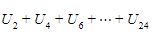 adalah 900.
adalah 900.
Jadi, jawaban yang tepat adalah C.

2) Topik : Aljabar Saintek
Subtopik : Sistem Persamaan dan Pertidaksamaan
Diketahui sistem persamaan berikut ini.
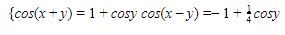
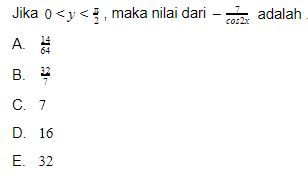
Jawaban: E
Pembahasan:
Dapat diperhatikan bahwa sistem persamaan pada soal dapat dituliskan menjadi dua persamaan sebagai berikut.
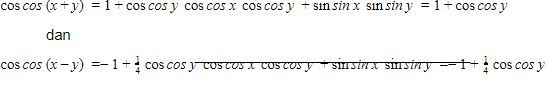
Kemudian, eliminasi sin sin x sin sin y sebagai berikut.
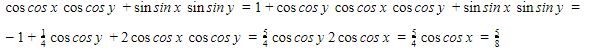

Jadi, jawaban yang tepat adalah E.
Baca juga: Latihan Soal dan Pembahasan UTBK 2022: TPS Penalaran Umum

3)Topik : Trigonometri Saintek
Subtopik : Pertidaksamaan Trigonometri
Untuk 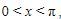 penyelesaian dari pertidaksamaan
penyelesaian dari pertidaksamaan 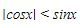

Jawaban: A
Pembahasan:
Perhatikan bahwa 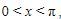 sehingga, x berada di kuadran I atau II. Akibatnya, sin x akan bernilai bernilai positif.
sehingga, x berada di kuadran I atau II. Akibatnya, sin x akan bernilai bernilai positif.
Kemudian, perhatikan bahwa 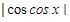 pasti tidak bernilai negatif, maka kedua ruas pada pertidaksamaan dapat dikuadratkan tanpa mengubah tanda pertidaksamaannya, menjadi
pasti tidak bernilai negatif, maka kedua ruas pada pertidaksamaan dapat dikuadratkan tanpa mengubah tanda pertidaksamaannya, menjadi
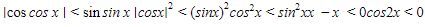
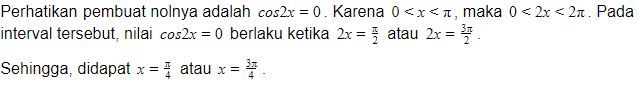
Perhatikan garis bilangan berikut!
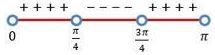
Karena tanda pertidaksamaannya adalah <, maka pilih daerah yang bernilai negatif, yaitu 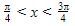
Sehingga, penyelesaian dari pertidaksamaan 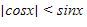 adalah
adalah 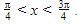
Jadi, jawaban yang tepat adalah A.

4) Topik : Geometri Saintek
Subtopik : Transformasi Geometri
Jika 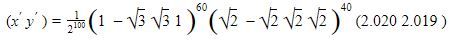 , maka nilai dari
, maka nilai dari ![]() adalah
adalah
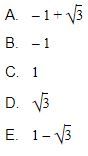
Jawaban: C
Pembahasan:
Perhatikan bahwa
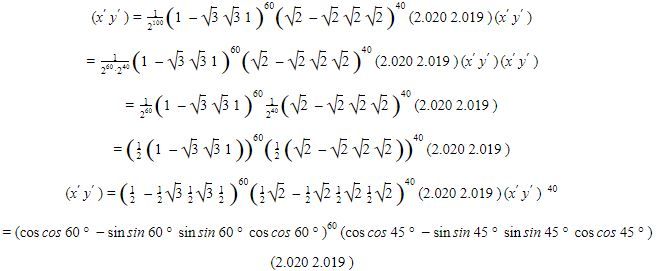
Sehingga persamaan 
dapat diartikan sebagai sebuah transformasi berupa rotasi pada titik (x, y)=2.020, 2.019 oleh matriks-matriks transformasi sebagai berikut:
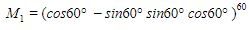 dan
dan 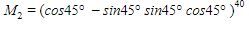




Topik : Kalkulus Saintek
Subtopik : Limit Fungsi
5. Jika 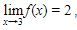 maka nilai dari
maka nilai dari 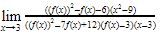 adalah..
adalah..
- -4
- -2
- 2
- 10
- 12
Jawaban: E
Pembahasan:
Perhatikan bahwa
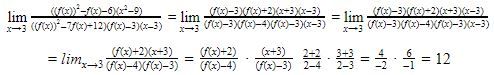
Jadi, jawaban yang tepat adalah E.
Baca juga: Latihan Soal dan Pembahasan UTBK 2022: TPS Pemahaman Bacaan

Topik : Teori Peluang Saintek
Subtopik : Kaidah Pencacahan dan Peluang Kejadian
6. Banyaknya bilangan ribuan dengan angka pertama dan terakhir memiliki selisih 5 serta tidak ada angka yang berulang adalah ….
- 504
- 576
- 648
- 729
- 900
Jawaban: E
Pembahasan:
Perhatikan gambar berikut!
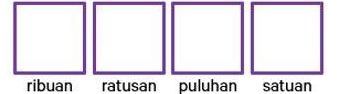
Angka pertama dan terakhir memiliki selisih 5. Sehingga, selisih angka ribuan dan angka satuannya adalah 5.
Diumpamakan
angka ribuan<angka satuan
dengan selisih angka ribuan oleh angka satuan adalah 5. Maka, didapat beberapa kemungkinan sebagai berikut.

Sehingga, ada 4 kemungkinan. Selanjutnya, diumpamakan
angka ribuan>angka satuan
dengan selisih angka satuan oleh angka ribuan adalah 5. Maka, didapat beberapa kemungkinan sebagai berikut.
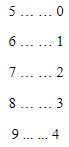
Sehingga, ada 5 kemungkinan. Secara total terdapat 9 kemungkinan untuk angka ribuan dan angka satuan.
Karena tidak boleh ada angka yang berulang, maka banyaknya angka yang mungkin untuk angka ratusan adalah 8 buah (didapat dari total angka 10 buah, namun dikurang 1 angka yang telah dipakai untuk angka ribuan, dan dikurang 1 lagi yang telah dipakai untuk angka satuan).
Kemudian, dengan cara yang serupa, didapat untuk angka puluhan tersisa 7 buah angka. Sehingga, secara total, terdapat 9×8×7=504 kemungkinan.
Jadi, jawaban yang tepat adalah A

Topik : Aljabar Saintek
Subtopik : Vektor
7. Diketahui titik A-x, -11, B7, x+1, dan C-1, 2x-3 dengan x adalah bilangan bulat. Jika 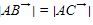 maka nilai dari
maka nilai dari 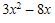 adalah..
adalah..
- 124
- 128
- 129
- 256
- 258
Jawaban: B
Pembahasan:
Perhatikan bahwa titik 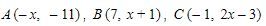 dapat dinyatakan dalam vektor posisi terhadap titik O dengan notasi masing-masing adalah
dapat dinyatakan dalam vektor posisi terhadap titik O dengan notasi masing-masing adalah 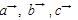 sebagai berikut:
sebagai berikut:
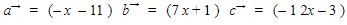
Dengan demikian, vektor ![]() dapat dicari sebagai berikut:
dapat dicari sebagai berikut:
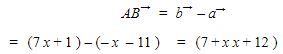
Kemudian, vektor ![]() dapat dicari dengan cara sebagai berikut:
dapat dicari dengan cara sebagai berikut:
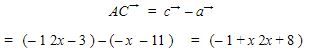
Akibatnya, didapat hasil perhitungan sebagai berikut.
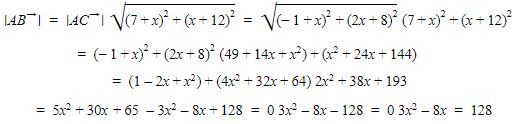
Jadi, jawaban yang tepat adalah B.

Topik : Aljabar Saintek
Subtopik : Persamaan Lingkaran
8. Lingkaran L yang memiliki titik pusat di kuadran I, menyinggung sumbu-x dan menyinggung lingkaran 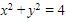 . Jika lingkaran L melalui titik (4, 6), maka persamaan dari lingkaran L yang tepat adalah ….
. Jika lingkaran L melalui titik (4, 6), maka persamaan dari lingkaran L yang tepat adalah ….
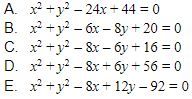
Jawaban: C
Pembahasan:
Dapat diperhatikan bahwa lingkaran 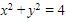 memiliki pusat di titik (0, 0) dan jari-jari dengan panjang 2 satuan. Diketahui lingkaran L memiliki titik pusat di kuadran I.
memiliki pusat di titik (0, 0) dan jari-jari dengan panjang 2 satuan. Diketahui lingkaran L memiliki titik pusat di kuadran I.
Misal lingkaran L yang bersinggungan dengan sumbu- memiliki pusat pada titik (a, b) maka didapat gambar sebagai berikut.
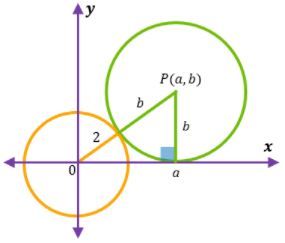
(Catatan: Gambar di atas adalah ilustrasi apabila a>b).
Karena titik pusat lingkaran L berada di kuadran I, maka a>0 dan b>0. Dapat diperhatikan bahwa panjang jari-jari lingkaran L adalah b satuan. Berdasarkan gambar di atas, dapat diterapkan Teorema Pythagoras sebagai berikut.
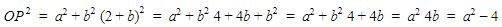
Karena lingkaran L berpusat pada titik (a, b) dan panjang jari-jari lingkaran L adalah b satuan, maka persamaan lingkaran L dapat ditulis sebagai berikut.
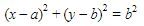
Karena lingkaran L melalui titik (4, 6) maka didapat perhitungan sebagai berikut.
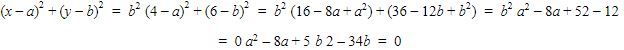
Karena 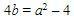 maka didapat perhitungan sebagai berikut.
maka didapat perhitungan sebagai berikut.
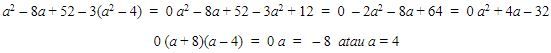
Karena a>0, maka a=4. Oleh karena itu, didapat perhitungan sebagai berikut.
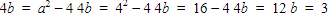
Oleh karena itu, didapat persamaan lingkaran L adalah sebagai berikut.
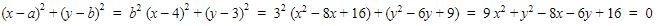
Jadi, jawaban yang tepat adalah C.

Topik : Kalkulus Saintek
Subtopik : Limit
9. Diberikan fungsi ![]() dan
dan ![]() yang kontinu untuk seluruh bilangan real. Jika
yang kontinu untuk seluruh bilangan real. Jika  maka nilai dari
maka nilai dari 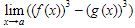 adalah..
adalah..
- 26
- 27
- 63
- 64
- 65
Jawaban: C
Pembahasan:
Perhatikan bahwa
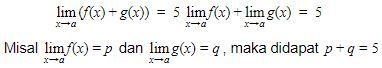
Kemudian, perhatikan perhitungan berikut!
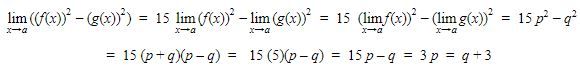
Oleh karena itu, didapat perhitungan sebagai berikut.
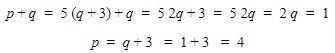
Dengan demikian, didapat hasil perhitungan sebagai berikut.
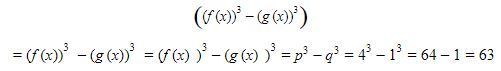
Jadi, jawaban yang tepat adalah C.
Baca juga: Latihan Soal dan Pembahasan UTBK 2021: Fisika

Topik : Geometri Saintek
Subtopik : Transformasi Geometri
10. Untuk ![]() , hasil dari
, hasil dari 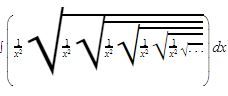 adalah…
adalah…
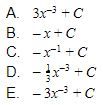
Jawaban: D
Pembahasan:
Misal 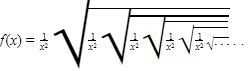
Dapat diperhatikan bahwa fungsi tersebut dapat dituliskan sebagai berikut.
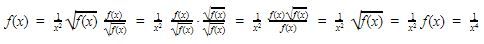
Oleh karena itu, didapat
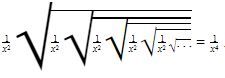
Dengan demikian, didapat hasil integralnya adalah sebagai berikut
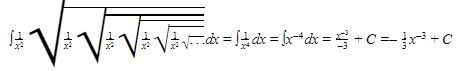
Jadi, jawaban yang tepat adalah D.

Akhirnya selesai juga~ Kamu capek gak? Istirahat sebentar gak dilarang kok. Selain materi TKA dan TPS, kesehatan juga perlu diperhatikan untuk menghadapi UTBK 2021. Kalau pengen curhat persiapan kuliah, langsung aja ngobrol bareng kakak konselor di ruangles. Semoga membantu!
















