Latihan Soal PTS Kelas 11 SMA IPA Semester Ganjil 2023 & Pembahasannya

Yuhuuu, siapa yang udah nungguin latihan soal dan pembahasan PTS Semester Ganjil 2023 untuk kelas 11 IPA? Yuk, kerjakan soalnya lalu simak pembahasannya, ya!

—

 

Guys, PTS Semester Ganjil 2023 udah di depan mata nih, sudah sejauh apa persiapanmu? Nah, selagi mempelajari materi-materi yang sudah pernah dibahas di sekolah, kamu juga perlu mengerjakan latihan soal ya, supaya persiapanmu jadi semakin matang. Yuk, langsung aja kerjakan latihan soal berikut ini!

BIOLOGI

 

Topik: Sel

Subtopik: Organel sel

Konsep: Struktur mitokondria

Level: Medium

 

1. Perhatikan fungsi organel sel di bawah ini!

1. 1. Respirasi sel
2. 2. Detoksifikasi
3. 3. Dehidrogenasi
4. 4. Oksidasi makanan
5. 5. Autolisis

 

Fungsi mitokondria ditunjukkan oleh nomor ….

a. 1, 2, dan 3
b. 1, 3, dan 4
c. 2, 3, dan 4
d. 1, 3, dan 5
e. 1, 4 dan 5

 

 

 

Jawaban: B

Pembahasan:

Mitokondria merupakan organel berbentuk oval yang mana bagian dalam organel mitokondria berbentuk lekukan-lekukan atau lipatan-lipatan. Fungsi mitokondria adalah sebagai berikut.

• – Respirasi sel untuk menghasilkan energi atau ATP
• – Oksidasi makanan
• – Dehidrogenasi
• – Fosforilasi oksidatif
• – Sistem transpor elektron

 

Dengan demikian, pilihan jawaban yang tepat adalah B.

Topik: Sel

Subtopik: Komponen kimiawi sel 

Konsep: Komponen air pada sel

Level: Medium

 

2. Komponen kimiawi anorganik terbanyak yang penyusun sel dan memiliki peran dalam mempercepat suatu reaksi di dalam sel adalah ….

a. air
b. vitamin
c. mineral
d. protein
e. karbohidrat

 

 

 

Jawaban: A

Pembahasan:

Air merupakan komponen kimia terbanyak penyusun sel. Di dalam sel, air berperan sebagai pelarut, medium berbagai reaksi kimia di dalam sel, serta mempercepat reaksi biologi di dalam sel.

Dengan demikian, pilihan jawaban yang tepat adalah A.

Topik: Sel

Subtopik: Transpor membran

Konsep: Definisi osmosis

Level: HOTS

 

3. Perhatikan gambar di bawah ini!

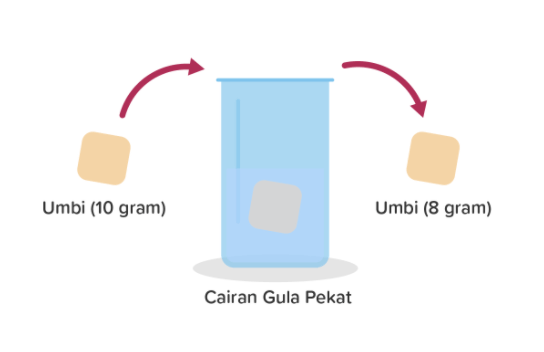
Hal yang menyebabkan perubahan berat dari umbi setelah direndam dalam cairan gula pekat adalah …. 

a. peristiwa difusi, dimana cairan gula pekat bersifat hipertonis dan cairan dalam sel umbi bersifat hipotonis
b. peristiwa osmosis, dimana cairan gula pekat bersifat hipotonis dan cairan dalam sel umbi bersifat hipertonis
c. peristiwa difusi, dimana cairan gula pekat bersifat hipotonis dan cairan dalam sel umbi bersifat hipertonis
d. peristiwa osmosis, dimana cairan gula pekat bersifat hipertonis dan cairan dalam sel umbi bersifat hipotonis
e. peristiwa osmosis, dimana cairan gula pekat dan cairan dalam sel umbi bersifat isotonis

 

 

 

Jawaban: D

Pembahasan:

Proses yang terjadi pada gambar menunjukkan pengurangan massa umbi dari 10 gram ke 8 gram setelah dilakukan perendaman dalam larutan cairan gula pekat. Terjadinya penurunan massa ini diduga karena cairan dari dalam sel umbi mengalir keluar menuju larutan pekat. Proses keluarnya cairan dari dalam sel umbi ini terjadi melalui proses osmosis. Osmosis merupakan perpindahan pelarut dari konsentrasi pelarut tinggi (larutan encer atau hipotonis) ke konsentrasi pelarut rendah (larutan pekat atau hipotonis) melewati membran semipermeabel. Sehingga, dapat disimpulkan hal yang menyebabkan perubahan berat dari umbi adalah peristiwa osmosis, dimana cairan gula pekat bersifat hipertonis dan cairan pada sel umbi bersifat hipotonis.

Dengan demikian, pilihan jawaban yang benar adalah D.

Topik: Struktur dan Fungsi Jaringan pada Tumbuhan

Subtopik: Jaringan Sekretori

Konsep: Jaringan latisifer tidak beruas, Jaringan latisifer beruas

Level: Medium

 

4. Berdasarkan sel penyusunnya, jaringan latisifer pada tumbuhan dapat dibedakan menjadi ….

a. latisifer bercabang dan tidak bercabang
b. latisifer glanduler dan non-glanduler
c. latisifer inti tunggal dan inti banyak
d. latisifer beruas dan tidak beruas
e. sel lateks dan jaringan lateks

 

 

 

Jawaban: D

Pembahasan:

Berdasarkan sel penyusunnya, jaringan latisifer pada tumbuhan dapat dibedakan menjadi latisifer beruas dan tidak beruas. Latisifer tidak beruas disebut juga sebagai sel lateks karena hanya tersusun atas satu sel yang memanjang dengan banyak inti. Latisifer tidak beruas atau sel lateks ini nantinya masih dibedakan lagi menjadi bercabang dan tidak bercabang, berdasarkan pada ada tidaknya percabangan.

Dengan demikian, pilihan jawaban yang tepat adalah D.

Topik: Struktur dan Fungsi Jaringan pada Hewan

Subtopik: Jaringan Ikat

Konsep: Jaringan Ikat

Level: Medium

 

5. Rogu menemukan sebuah jaringan yang memiliki ciri tersusun oleh sel dan cairan, memiliki kemampuan untuk menembus dinding pembuluh darah menuju jaringan, dan berfungsi untuk mengangkut hormon. Jaringan yang memiliki ciri tersebut tergolong ke dalam ….

a. jaringan saraf
b. jaringan ikat
c. jaringan penyokong
d. jaringan ikat longgar
e. jaringan otot

 

 

 

Jawaban: B

Pembahasan:

Jaringan yang memiliki ciri tersusun oleh sel dan cairan, memiliki kemampuan untuk menembus dinding pembuluh darah menuju jaringan, dan berfungsi untuk mengangkut hormon adalah jaringan darah. Jaringan darah termasuk ke dalam jaringan ikat, yaitu jaringan ikat cair.

Dengan demikian, pilihan jawaban yang tepat adalah B.

Topik: Struktur dan Fungsi Jaringan Tumbuhan

Subtopik: Jaringan Penyokong

Level Kognitif: MOTS

 

6. Perhatikan karakteristik jaringan tumbuhan berikut!

1. Memiliki nukleus
2. Mengandung lignin
3. Kaku dan sangat kuat
4. Tidak menyisakan ruang antar sel
5. Kekuatan berasal dari tekanan turgor
6. Dapat ditemukan pada serabut kelapa
7. Mengalami penebalan primer yang tidak merata

Karakteristik dari sklerenkim ditunjukkan oleh nomor ….
a. 2, 3, 4, dan 6
b. 2, 5, 6, dan 7
c. 1, 2, 4, dan 5
d. 1, 3, 5, dan 7
e. 1, 3, 4. dan 6

 

 

 

Kunci Jawaban: A

Pembahasan:

Sklerenkim merupakan jaringan penyokong yang berfungsi untuk menyokong tubuh tumbuhan. Karakteristik dari jaringan sklerenkim adalah sebagai berikut:
– tersusun atas sel mati saat dewasa
– tidak memiliki nukleus
– mengalami penebalan sekunder yang merata
– tidak menyisakan ruang antar sel
– mengandung lignin
– kaku dan sangat kuat
– kekuatan berasal dari lignifikasi
– dapat ditemukan pada organ sudah dewasa, misalnya serabut kelapa, serabut tumbuhan rami, dan kulit biji

Berdasarkan informasi tersebut, karakteristik dari sklerenkim ditunjukkan oleh nomor 2, 3, 4, dan 6. Sementara itu, nomor 1, 5, dan 7 adalah ciri dari jaringan penyokong kolenkim.

Dengan demikian, pilihan jawaban yang tepat adalah A.

Baca Juga: Latihan Soal PTS Kelas 11 SMA IPA Semester Genap Tahun 2023

KIMIA

 

Topik: Hidrokarbon 

Subtopik: Hidrokarbon dalam Kehidupan

 

1. Berikut ini zat atau bahan yang banyak digunakan dalam kehidupan sehari-hari.

1. 1. Polivinil klorida
2. 2. Kloroform
3. 3. Isoprena
4. 4. Asetilena

 

Pasangan senyawa yang tergolong haloalkana adalah ….

a. 1 dan 2
b. 1 dan 3
c. 1 dan 4
d. 2 dan 3
e. 2 dan 4

 

 

 

Jawaban: A

Pembahasan:

Haloalkana adalah senyawa alkana yang mengandung satu atau lebih unsur halogen (F, Cl, Br, dan I).

1. 1. Polivinil klorida = C2H3Cln
2. 2. Kloroform = CHCl3
3. 3. Isoprena =C5H8
4. 4. Asetilena =C2H2

 

Senyawa 1 dan 2 tergolong haloalkana, sedangkan senyawa 3 dan 4 tergolong hidrokarbon.

Jadi, jawaban yang tepat adalah A.

Topik: Hidrokarbon 

Subtopik: Reaksi Senyawa Hidrokarbon

 

2. Perhatikan senyawa berikut!

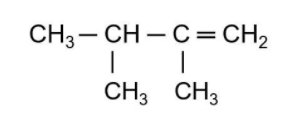
Senyawa hidrokarbon dapat mengalami beberapa reaksi, yaitu reaksi substitusi, eliminasi, dan adisi. Jika senyawa di atas direaksikan dengan HCl, akan menghasilkan ….

a. 2,3-dimetil-2-klorobutana
b. 2-kloro-2,3-dimetilbutana
c. 2,3-dimetil-1-klorobutana
d. 2,3-dimetil-2-klorobutena
e. 2-kloro-2,3-dimetilbutena

 

 

 

Jawaban: B

Pembahasan:

Jika senyawa alkena dan alkuna direaksikan dengan golongan halogen, akan terjadi reaksi adisi. Reaksi adisi adalah reaksi penambahan atom. Ciri dari reaksi adisi adalah pengurangan ikatan rangkap. Alkuna diadisi akan membentuk alkena, sedangkan alkena jika diadisi akan membentuk alkana. Alkana tidak dapat diadisi karena tidak memiliki ikatan rangkap.

Pada reaksi adisi ini, berlaku hukum Markovnikov. Atom H dari HCl akan masuk ke atom karbon rangkap yang mengikat lebih banyak atom H. Reaksi yang terjadi adalah sebagai berikut.

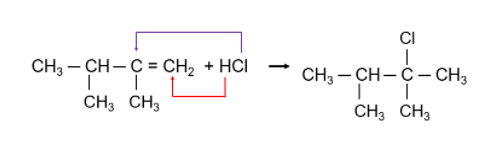
Berikut ini penomoran dari produk yang dihasilkan.

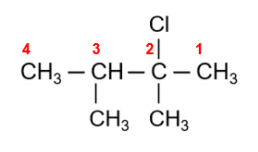
Nama senyawa yang terbentuk dari reaksi tersebut adalah 2-kloro-2,3-dimetilbutana. Cabang kloro ditulis terlebih dahulu karena diserap dari kata chloro yang memiliki awalan “c”.

Jadi, jawaban yang tepat adalah B.

Topik: Minyak Bumi 

Subtopik: Minyak Bumi dan Fraksi Penting Minyak Bumi

 

3. Data penyulingan minyak mentah adalah sebagai berikut.

1. 1. Pemanasan pada 140°C-180°C
2. 2. Pemanasan pada 180°C-250°C
3. 3. Pemanasan pada 250°C-350°C

 

Urutan fraksi minyak bumi yang diperoleh dari minyak mentah, dari yang teringan hingga terberat secara berurutan adalah ….

a. nafta – kerosin – solar
b. kerosin – solar – nafta
c. solar – nafta – kerosin
d. kerosin – nafta – solar
e. solar – kerosin – nafta

 

 

 

Jawaban: A

Pembahasan:

Berikut ini analisis fraksi minyak bumi pada suhu tertentu.

• – Pemanasannya pada 140°C-180°C –> nafta
• – Pemanasannya pada 180°C-250°C –> kerosin
• – Pemanasannya pada 250°C-350°C –> solar

Fraksi minyak bumi yang dipanaskan pada suhu lebih rendah artinya akan menguap lebih dahulu dan memiliki jumlah atom C lebih sedikit dibandingkan dengan fraksi yang dipanaskan pada suhu lebih tinggi. Oleh karena itu, urutan fraksi minyak bumi dari yang teringan hingga yang terberat secara berurutan, yaitu nafta – kerosin – solar.

Jadi, jawaban yang tepat adalah A.

Topik: Termokimia 

Subtopik: Energi dan Perubahan Energi

 

4. Suatu campuran antara air panas dan gula yang dimasukan ke dalam gelas akan menyebabkan gelas menjadi panas. Pada peristiwa ini terjadi ….

a. reaksi eksoterm
b. reaksi endoterm
c. reaksi reduksi
d. reaksi perubahan entalpi
e. reaksi perubahan entalpi standar

 

 

 

Jawaban: A

Pembahasan:

Pada reaksi antara air panas dengan gula yang menyebabkan gelas menjadi panas merupakan contoh dari reaksi eksoterm.  Reaksi eksoterm ditandai dengan kenaikan suhu (keadaan gelas yang menjadi tempat terjadinya reaksi menjadi panas).

Jadi, jawaban yang tepat adalah A.

Topik: Termokimia 

Subtopik: Penentuan Perubahan Entalpi

 

5. Diketahui data perubahan entalpi pembentukan standar H₂O(l)= -285 kJ/mol, CO₂(g)= -393 kJ/mol, dan C₂H₄(g)= +52,5 kJ/mol. Jumlah kalor yang dibebaskan pada pembakaran 1,4 g gas C₂H₄ (M_r=28) adalah ….

a. 26,23 kJ
b. 47,34 kJ
c. 70,43 kJ
d. 28.170 kJ
e. 110,25 kJ

 

 

 

Jawaban: C

Pembahasan:

Reaksi pembakaran 1 mol C₂H₄:

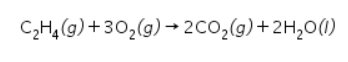
Perubahan entalpi reaksinya dapat dihitung sebagai berikut.

Hitung jumlah mol untuk 1,4 g gas C₂H₄.

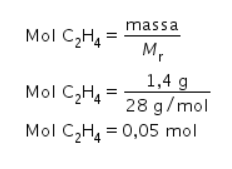
Kalor pembakaran 1,4 g gas C₂H₄, yaitu sebagai berikut.

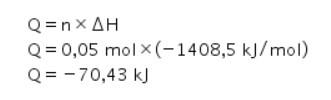
Tanda minus (-) artinya terjadi pelepasan kalor.

Jadi, jawaban yang tepat adalah C.

Topik: Hidrokarbon

Subtopik: Isomer

Level Kognitif: HOTS

 

6. Senyawa berikut yang memiliki isomer cis trans adalah ….
a. 3-etil-2-metil-2-pentena
b. 4-metil-2-pentena
c. 2-metil-1-butena
d. 1-butena
e. 1-propena

 

 

 

Kunci Jawaban: B

Pembahasan:

Isomer cis-trans atau isomer geometri merupakan isomer yang terjadi pada molekul yang mempunyai rumus molekul sama, tetapi struktur ruangnya berbeda. Isomer cis-trans biasanya terjadi pada senyawa alkena dan sikloalkana. Pada senyawa alkena, isomer cis-trans terjadi jika dua atom C rangkap masing-masing mengikat dua gugus yang berbeda. Isomer cis terjadi jika posisi kedua atom hidrogen letaknya sejajar, sedangkan isomer trans terjadi jika posisi kedua atom hidrogen letaknya berseberangan. Struktur senyawa 4-metil-2-pentena dapat digambarkan sebagai berikut.

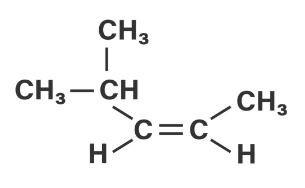
Berdasarkan strukturnya, atom C rangkap mengikat dua gugus yang berbeda. Oleh karena dua atom hidrogen terikat di dua atom C rangkap yang berbeda, isomer cis-trans dapat ditinjau dari posisi atom hidrogennya. Isomer cis-trans dari senyawa 4-metil-2-pentena adalah sebagai berikut.

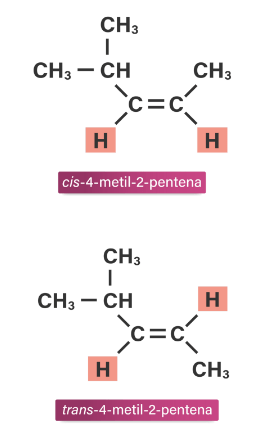
Ingat! Isomer cis terjadi ketika kedua atom hidrogen terletak sejajar, sedangkan isomer trans terjadi ketika kedua atom hidrogen terletak berseberangan. Pada senyawa di opsi A, C, D, dan E, dua atom C rangkap masing-masing mengikat dua gugus yang sama sehingga keempat senyawa tersebut tidak memiliki isomer cis-trans.

Jadi, jawaban yang benar adalah B.

Baca Juga: Latihan Soal dan Pembahasan PTS Kelas 11 IPA Semester Genap 2021

FISIKA

 

Topik: Kesetimbangan dan Dinamika Rotasi

Subtopik: Momen Gaya

Level: MOTS

 

1. Perhatikan gambar berikut ini!

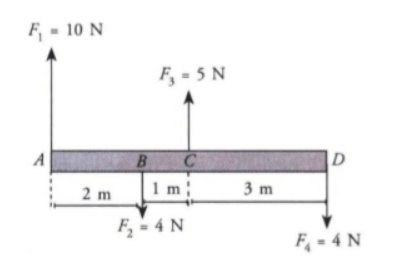
Jika massa batang diabaikan, nilai momen gaya terhadap titik D adalah ….

a. 17 Nm
b. 23 Nm
c. 29 Nm
d. 31 Nm
e. 59 Nm

 

 

 

Jawaban: E

Pembahasan:

Kesepakatan tanda yang digunakan:

• – searah jarum jam bernilai negatif (-)
• – berlawanan arah jarum jam bernilai positif (+).

Momen gaya terhadap titik D dapat diketahui dengan

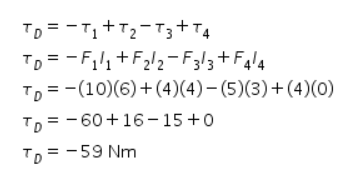
Tanda minus hanya menunjukkan arah momen gaya, yaitu searah dengan putaran jarum jam. Dengan demikian, nilai momen gaya terhadap titik D adalah 59 N m.

Jadi, jawaban yang tepat adalah E.

Topik: Kesetimbangan dan Dinamika Rotasi

Subtopik: Energi Kinetik

Level: HOTS

 

2. Sebuah silinder tipis berongga dengan jari-jari 20 cm dan bermassa 1 kg bergerak dengan kelajuan awal sebesar 10 m/s menaiki sebuah bidang miring kasar. Jika saat menaiki bidang miring tersebut silinder selalu menggelinding dan tidak pernah tergelincir, ketinggian maksimum yang dapat dicapai oleh silinder adalah ….

a. 1 m
b. 2 m
c. 5 m
d. 8 m
e. 10 m

 

 

 

Jawaban: E

Pembahasan:

Diketahui:

m = 1 kg

R = 20 cm = 0,2 m

v = 10 m/s

Ketinggian maksimum yang dapat dicapai silinder berongga dapat diketahui dengan menggunakan hukum kekekalan energi mekanik. Energi mekanik silinder di posisi awal sama dengan energi mekaniknya ketika berada di posisi akhir.

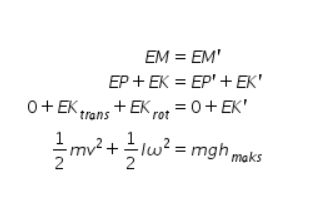
Kita ketahui persamaan momen inersia silinder tipis berongga adalah 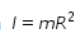, dan kecepatan sudut dapat diuraikan menjadi 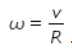. Sehingga persamaannya berubah menjadi:

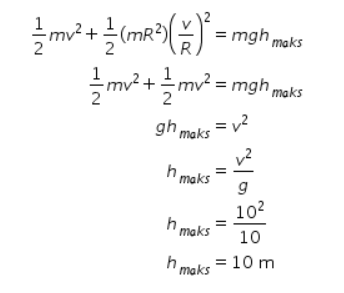
Jadi, jawaban yang tepat adalah E.

Topik: Elastisitas dan Hukum Hooke

Subtopik: Rangkaian Pegas

Level: MOTS

 

3. Delapan pegas identik memiliki konstanta masing-masing 250 N/m. Empat pegas disusun secara seri dan empat pegas lainnya disusun secara paralel. Perbandingan konstanta pegas yang disusun secara seri dan paralel sebesar ….

a. 1 : 4
b. 1 : 8
c. 1 : 16
d. 4 : 1
e. 8 : 1

 

 

 

Jawaban: C

Pembahasan:

Diketahui:

k = 250 N/m

Konstanta pegas pengganti yang disusun secara paralel adalah:

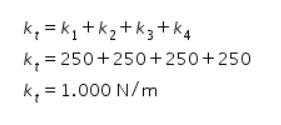
Konstanta pegas pengganti yang disusun secara seri adalah:

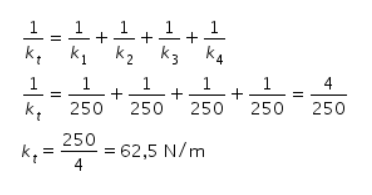
Sehingga perbandingan konstanta pegas seri dan paralel yaitu:

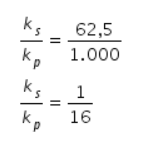
Jadi, jawaban yang tepat adalah C.

Topik: Elastisitas dan Hukum Hooke

Subtopik: Tegangan

Level: LOTS

 

4. Tegangan yang dialami oleh seutas kawat yang memiliki luas penampang 4 cm² dan dikenai gaya sebesar 6 N adalah ….

a. 0,5 x 10⁴ N/m²

b. 1,0 x 10⁴ N/m²

c. 1,5 x 10⁴ N/m²

d. 2,0 x 10⁴ N/m²

e. 2,5 x 10⁴ N/m²

 

 

 

Jawaban: C

Pembahasan:

Diketahui:

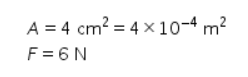
Tegangan yang dialami oleh kawat dapat dihitung dengan persamaan

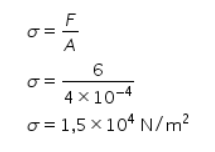
Jadi, jawaban yang tepat adalah C.

Topik: Fluida Statis

Subtopik: Hukum Pascal

Level: MOTS

 

5. Sebuah pompa hidrolik memiliki pengisap input dengan jari-jari 5 mm dan pengisap output dengan jari-jari 20 mm. Jika gaya sebesar 50 N digunakan pada pengisap input, gaya yang dapat dihasilkan pada pengisap output sebesar ….

a. 12,5 N
b. 50 N
c. 200 N
d. 800 N
e. 1.200 N

 

 

 

Jawaban: D

Pembahasan:

Diketahui:

 

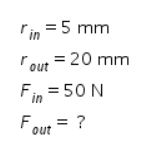
Berdasarkan hukum Pascal, tekanan pada pengisap input sama dengan tekanan pada pengisap output. Persamaannya dapat dinyatakan sebagai berikut:

 

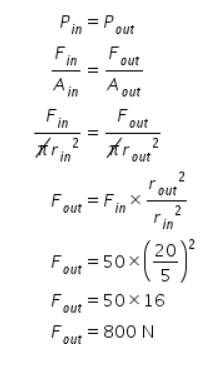
Dengan demikian, gaya yang dapat dihasilkan pada pengisap output sebesar 800 N.

Jadi, jawaban yang tepat adalah D.

Topik: Elastisitas dan Hukum Hooke

Subtopik: Rangkaian Pegas

Level Kognitif: HOTS

 

6. Tiga pegas identik dirangkai seri kemudian digantungkan beban bermassa 200 gram, sehingga rangkaian pegas bertambah panjang sebesar 3 cm. Jika ketiga pegas kemudian dirangkai paralel dan massa beban ditambah 400 gram dari semula, besar pertambahan panjang yang dialami rangkaian pegas adalah ….
a. 1 cm
b. 2 cm
c. 3 cm
d. 4 cm
e. 5 cm

 

 

 

Kunci Jawaban: A

Pembahasan:

Diketahui:

F merupakan gaya tarik pada pegas dan pada kasus ini gaya tarik berasal dari gaya berat beban w, sehingga F = w. Untuk menentukan pertambahan panjang pegas kedua dapat dihitung dengan menggunakan perbandingan nilai sebagai berikut.

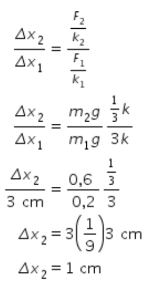
Jadi, jawaban yang benar adalah A.

Topik: Kesetimbangan dan Dinamika Rotasi

Subtopik: Hubungan antara Momen Gaya dan Momen Inersia

Level Kognitif: MOTS

 

7. Sebuah batang homogen dengan panjang 60 cm memiliki total momen gaya 15 Nm. Jika poros putar berada di ujung batang dan percepatan sudut sistem 6,25 rad/s², massa batang homogen tersebut adalah ….
a. 2 kg
b. 4 kg
c. 10 kg
d. 20 kg
e. 25 kg

 

 

 

Kunci Jawaban: D

Pembahasan:

Diketahui:

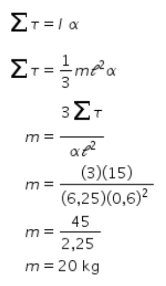
Jadi, jawaban yang tepat adalah D.

Baca Juga: Latihan Soal PTS Kelas 11 IPA Semester Ganjil 2022

MATEMATIKA

 

Topik: Induksi Matematika

Subtopik: Induksi Matematika 2 (Ketidaksamaan)

Level: HOTS

 

1. Diketahui pernyataan-pernyataan sebagai berikut.

1. 1. n²-5>2n-3 untuk setiap bilangan bulat n>2.
2. 2. 2n²+1>5n+4 untuk setiap bilangan bulat n≥3.

 

Dengan menggunakan prinsip induksi matematika, pernyataan yang bernilai benar ditunjukkan oleh nomor ….

a. 1 saja
b. 2 saja
c. 1 dan 2
d. Tidak keduanya
e. Tidak dapat ditentukan

 

 

 

Jawaban: A

Pembahasan:

Pernyataan 1

Perhatikan pernyataan berikut!

P_n : n²-5>2n-3

untuk setiap bilangan bulat n>2.

Karena akan dibuktikan pernyataan untuk setiap bilangan bulat n>2 atau n≥3, maka langkah pertamanya adalah buktikan P₃ benar.

 

LANGKAH 1: Buktikan P₃ benar.
Perhatikan pernyataan berikut!

P_n : n²-5>2n-3

Oleh karena itu, diperoleh pernyataan berikut.

P₃ : 3²-5>2(3)-3

Diperoleh nilai pada ruas kiri dan kanan berturut-turut, yaitu 3²-5=9-5=4 dan 2(3)-3=6-3=3. Karena nilai pada ruas kiri lebih besar dari nilai pada ruas kanan, maka P₃ benar.

LANGKAH 2: Buktikan untuk sembarang bilangan bulat k>2, jika P_k bernilai benar, maka mengakibatkan P_k+1 bernilai benar.

Perhatikan pernyataan berikut!

P_n : n²-5>2n-3

Asumsikan pernyataan berikut bernilai benar.

P_n : k²-5>2k-3

Perhatikan pernyataan berikut!

P_k+1 : (k+1)²-5>2(k+1)-3

Kemudian, perhatikan perhitungan pada ruas kiri P_k+1 sebagai berikut!

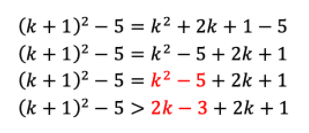
Karena k>2, maka 2k+1>5>2 sehingga diperoleh hubungan berikut.

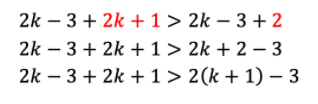
Dengan demikian, diperoleh pula hubungan berikut.

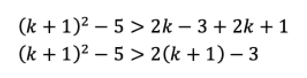
Perhatikan bahwa bentuk di atas merupakan pernyataan P_k+1 sehingga dapat disimpulkan bahwa P_k+1 bernilai benar.

Karena

1. 1. P₃ benar dan
2. 2. Untuk sembarang bilangan bulat k>2, jika P_k bernilai benar, maka mengakibatkan mengakibatkan P_k+1 bernilai benar,

 

maka Pn benar untuk setiap bilangan bulat n>2 menurut prinsip induksi matematika.

Pernyataan 2

Perhatikan pernyataan berikut!

P_n : 2n²+1>5n+4

untuk setiap bilangan bulat n≥3.

Karena akan dibuktikan pernyataan untuk setiap bilangan bulat n≥3, maka langkah pertamanya adalah buktikan P₃ benar.

LANGKAH 1: Buktikan P₃ benar.
Perhatikan pernyataan berikut!

P_n : 2n²+1>5n+4

Dengan demikian, diperoleh pernyataan berikut.

P₃ : 2(3)²+1>5(3)+4

Diperoleh nilai pada ruas kiri dan kanan berturut-turut, yaitu 2(3)²+1=29+1=18+1=19 dan 53+4=15+4=19. Karena nilai pada ruas kiri sama dengan nilai pada ruas kanan, maka P₃ salah.

Karena P₃ salah, maka P_n tidak bernilai benar untuk setiap bilangan bulat n≥3 menurut prinsip induksi matematika.

Oleh karena itu, dengan menggunakan prinsip induksi matematika, pernyataan yang bernilai benar ditunjukkan oleh nomor 1 saja.

Jadi, jawaban yang tepat adalah A.

Topik: Program Linear

Subtopik: Pemodelan Matematika

Level: Medium

 

2. Seorang anak diharuskan minum dua jenis tablet setiap hari. Tablet jenis I mengandung 5 unit vitamin A dan 3 unit vitamin B. Tablet jenis II mengandung 10 unit vitamin A dan 1 unit vitamin B. Dalam 1 hari, anak tersebut memerlukan minimal 25 unit vitamin A dan 5 unit vitamin B. Jika harga tablet I adalah Rp4.000,00 per butir dan harga tablet II adalah Rp8.000,00 per butir, maka biaya minimum untuk membeli tablet anak tersebut per hari adalah ….

a. Rp12.000,00
b. Rp14.000,00
c. Rp16.000,00
d. Rp18.000,00
e. Rp20.000,00

 

 

 

Jawaban: E

Pembahasan:

Dari informasi yang ada di soal, didapat tabel seperti di bawah ini.

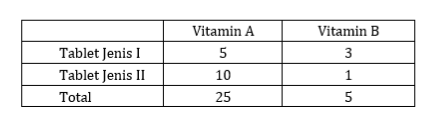
Dilakukan permisalan sebagai berikut.

x: banyak tablet jenis I
y: banyak tablet jenis II

Diketahui bahwa anak tersebut memerlukan minimal 25 unit vitamin A dan 5 unit vitamin B. Oleh karena itu, didapat sistem pertidaksamaan sebagai berikut.

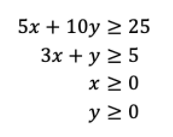
Kemudian, diketahui bahwa harga tablet I adalah Rp4.000,00 per butir dan harga tablet II Rp8.000,00 per butir. Oleh karena itu, fungsi objektifnya adalah sebagai berikut.

f(x, y) = 4.000x + 8.000y

Selanjutnya, daerah himpunan penyelesaian dari sistem pertidaksamaan tersebut dapat dicari sebagai berikut.

Dari pertidaksamaan 5x+10y≥25, didapat daerah penyelesaiannya berada di kanan garis 5x+10y=25.

Dari pertidaksamaan 3x+y≥5, didapat daerah penyelesaiannya berada di kanan garis 3x+y=5.

Dari pertidaksamaan x>0 dan y>0, didapat daerah penyelesaiannya berada di kuadran I (di atas sumbu-x dan di kanan sumbu-y).

Dengan demikian, daerah himpunan penyelesaiannya dapat digambarkan sebagai berikut.

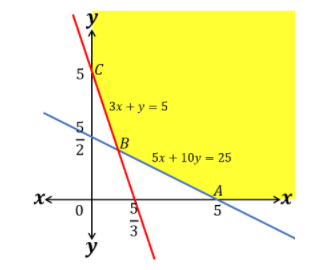
Didapatkan titik pojok A(5, 0) dan C(0, 5).

Selanjutnya, koordinat titik pojok B, yaitu titik potong antara garis 3x+y=5 dan garis 5x+10y=25 dapat ditentukan sebagai berikut.

Perhatikan bahwa dari 3x+y=5 , didapat persamaan sebagai berikut.

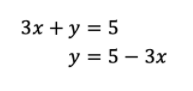
Substitusi y=5-3x ke persamaan 5x+10y=25 sehingga didapat hubungan sebagai berikut.

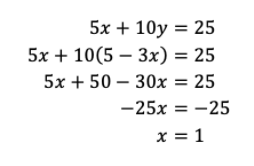
Kemudian, substitusi x=1 ke salah satu persamaan sehingga didapat nilai y sebagai berikut.

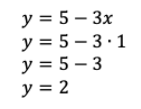
Jadi, koordinat titik B adalah (1, 2).

Selanjutnya, nilai minimum untuk f(x, y) = 4.000x + 8.000y dapat ditentukan sebagai berikut.

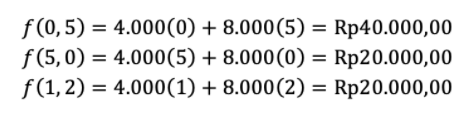
Didapatkan bahwa biaya minimum untuk membeli tablet anak tersebut per hari adalah Rp20.000,00.

Jadi, jawaban yang tepat adalah E.

Topik: Matriks

Subtopik: Operasi Hitung Matriks

Level: Medium

 

3. Jika (1 1 1 a b c)(-1 x -1 y -1 z) = (-3 3 3 6) , maka nilai dari ay+az+bx+bz+cx+cy adalah ….

a. -24
b. -15
c. 0
d. 12
e. 24

 

 

 

Jawaban: B

Pembahasan:

Perhatikan perhitungan berikut ini!

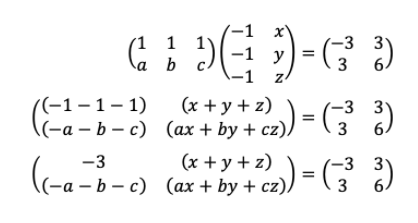
Dari kesamaan matriks di atas diperoleh persamaan-persamaan sebagai berikut.

Kemudian, perhatikan persamaan berikut!

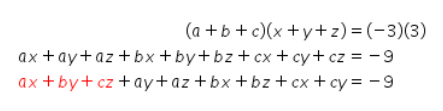
Ingat bahwa ax+by+cz=6 sehingga persamaannya menjadi seperti berikut.

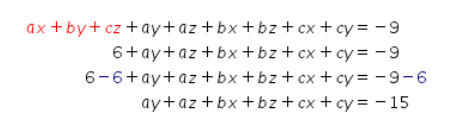
Dengan demikian, didapat ay + az + bx + bz + cx + cy = -15.

Jadi, jawaban yang tepat adalah B.

Topik: Persamaan Trigonometri

Subtopik: Persamaan Trigonometri Lanjutan

Level: Medium

4. Banyak nilai x yang memenuhi persamaan 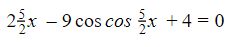dengan 0°<x<180° adalah … buah.

a. 5
b. 4
c. 3
d. 2
e. 0

 

 

 

Jawaban: C

Pembahasan:

Misalkan 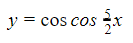  sehingga didapat perhitungan berikut ini.

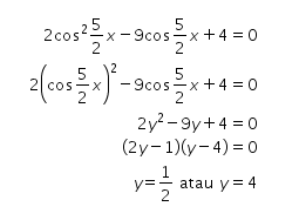
Substitusikan kembali nilai 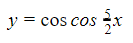 sehingga didapat hasil berikut ini.

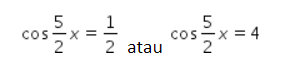
Ingat bahwa -1 ≤ cos cos α ≤ 1 untuk setiap α sehingga nilai cos cos  =4 tidak memiliki penyelesaian.

Jadi, perhatikan persamaan  =   saja.

Ingat bahwa cos cos 60° =  sehingga didapat nilai cos cos  = cos cos 60° .

Persamaan cos cos x = cos cos α terpenuhi oleh

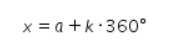
dan

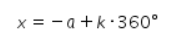
Dengan k∈N.

Oleh karena itu, persamaan cos cos  = cos cos 60°  terpenuhi oleh

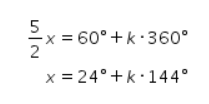
dan

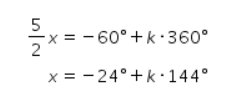
dengan k∈N.

Kemungkinan 1: x=24°+k∙144°, k∈N.

Jika k=-1, maka didapat perhitungan sebagai berikut.

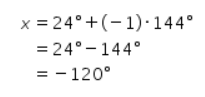
Karena -120° tidak memenuhi syarat dan -120° < 0°, maka untuk nilai k yang semakin kecil pasti akan didapat nilai x yang tidak memenuhi syarat juga.

Jika k=0, maka didapat x= 24° + 0∙144° = 24° sehingga nilai x = 24° memenuhi syarat.

Jika k=1, maka didapat perhitungan sebagai berikut.

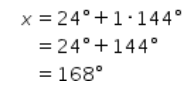
Didapat nilai x=168° memenuhi syarat.

Jika k=2, maka didapat perhitungan sebagai berikut.

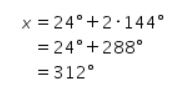
Karena 312° tidak memenuhi syarat dan 312°>180°, maka untuk nilai k yang semakin besar pasti akan didapat nilai x yang tidak memenuhi syarat juga.

Kemungkinan 2: x=-24°+k∙144°, k∈N.

Jika k=0, maka didapat x=-24°+0∙144°=-24°.

Karena -24° tidak memenuhi syarat dan -24°<0°, maka untuk nilai k yang semakin kecil pasti akan didapat nilai x yang tidak memenuhi syarat juga.

Jika k=1, maka didapat perhitungan sebagai berikut.

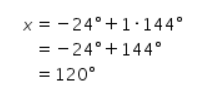
Didapat nilai x=120° memenuhi syarat.

Jika k=2, maka didapat perhitungan sebagai berikut.

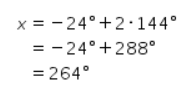
Karena 264° tidak memenuhi syarat dan 264°>180°, maka untuk nilai k yang semakin besar pasti akan didapat nilai x yang tidak memenuhi syarat juga.

Dengan demikian, diperoleh nilai-nilai x yang memenuhi yaitu 24°, 120°, dan 168° sehingga banyaknya nilai x yang memenuhi persamaan ada sebanyak 3 buah.

Jadi, jawaban yang tepat adalah C.

Topik: Minat – Trigonometri Analitika

Subtopik: Jumlah dan Selisih Dua Sudut

Level: HOTS

 

5. Perhatikan gambar berikut!

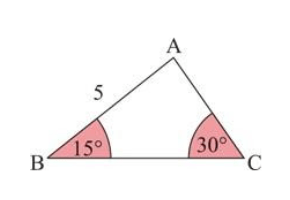
Panjang AC adalah ….

 

 

 

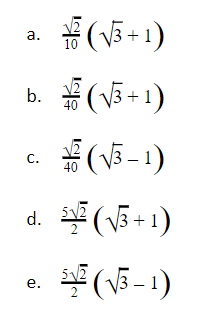
Jawaban: E

Pembahasan:

Perhatikan bahwa 15°=45°-30°. Oleh karena itu, nilai dari sin 15°  dapat ditentukan sebagai berikut.

Kemudian, dengan menggunakan aturan sinus, panjang AC dapat ditentukan sebagai berikut.

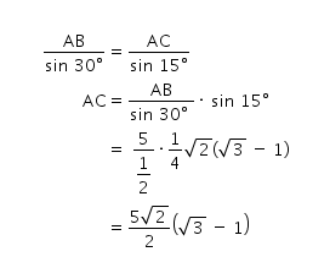
Jadi, jawaban yang tepat adalah E.

Topik: Induksi Matematika

Subtopik: Induksi Matematika 1 (Persamaan)

Level Kognitif: MOTS

 

6. Perhatikan pernyataan berikut!

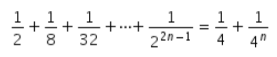
untuk setiap n bilangan asli. Dengan menggunakan induksi matematika, dapat disimpulkan bahwa …
a. Pernyataan tidak terbukti karena tahap pertama tidak bisa dibuktikan meskipun tahap kedua bisa dibuktikan.
b. Pernyataan tidak terbukti karena tahap kedua tidak bisa dibuktikan meskipun tahap pertama bisa dibuktikan.
c. Pernyataan tidak terbukti karena tahap pertama dan kedua tidak bisa dibuktikan.
d. Pernyataan terbukti dengan induksi matematika.
e. Tidak ada yang dapat disimpulkan.

 

 

 

Kunci Jawaban: B

Pembahasan:

Perhatikan pernyataan berikut!

Dengan demikian, pada proses pembuktian dengan induksi matematika tersebut, didapatkan bahwa pernyataan tidak terbukti karena tahap kedua tidak bisa dibuktikan meskipun tahap pertama bisa dibuktikan.

Jadi, jawaban yang tepat adalah B.

Topik: Program Linear

Subtopik: Aplikasi dan Latihan Soal Program Linear

Level Kognitif: MOTS

 

7. Diketahui sistem pertidaksamaan sebagai berikut.

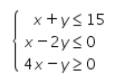
Nilai maksimum dari fungsi objektif f(x,y) = 3x + 2y adalah ….
a. 30
b. 33
c. 36
d. 40
e. 43

 

 

 

Kunci Jawaban: D

Pembahasan:

Pertama, gambarkan garis dari masing-masing pertidaksamaan dengan bantuan tabel berikut.

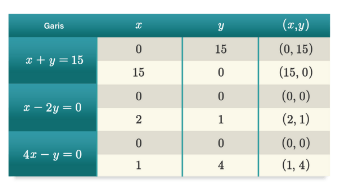
Didapatkan gambar seperti di bawah ini:

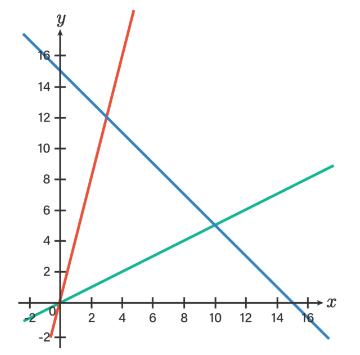
Untuk menentukan daerah penyelesaiannya, perhatikan lagi pertidaksamaannya.

Pada pertidaksamaan x + y ≤ 15, daerahnya berada di sebelah kiri garis x + y = 15 (garis biru).
Pada pertidaksamaan x – 2y ≤ 0, daerahnya berada di sebelah kiri garis x – 2y = 0 (garis hijau).
Pada pertidaksamaan 4x – y ≥ 0, daerahnya berada di sebelah kanan garis 4x – y = 0 (garis merah).

Oleh karena itu, diperoleh daerah penyelesaiannya adalah sebagai berikut.

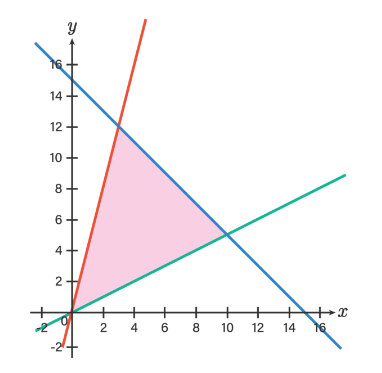
Dapat dilihat pada gambar, terdapat tiga titik pojok, yaitu (0,0) dan dua lagi adalah titik potong antara garis-garis tersebut.

Garis merah dan biru dapat ditentukan sebagai berikut.

Titik potong antara garis merah dan biru dapat ditentukan sebagai berikut.

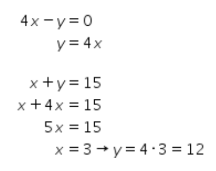
Didapat titik potong kedua garis tersebut adalah (3,12).

Kemudian, titik potong antara garis hijau dan biru dapat ditentukan sebagai berikut.

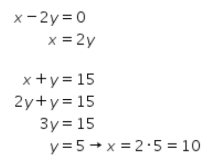
Didapat titik potong kedua garis tersebut adalah (10,5).

Berikutnya, substitusikan masing-masing titik pojok ke fungsi objektif f(x,y) = 3x + 2y sebagai berikut.

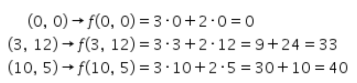
Dengan demikian, nilai maksimumnya adalah 40.

Jadi, jawaban yang tepat adalah D.

Nah, itu tadi latihan soal dan pembahasan PTS Semester Ganjil 2023 untuk kelas 11 IPA. Kalau kamu butuh latihan soal yang lebih banyak lagi, langsung meluncur aja ke ruangbelajar, ya! Di sana ada ribuan latihan soal yang bisa membantu kamu mempersiapkan diri menghadapi PTS, lho!