Barisan Aritmatika Bertingkat: Konsep Dasar, Rumus & Contoh Soal | Matematika Kelas 8

Artikel Matematika kelas 8 ini membahas mengenai barisan aritmatika bertingkat, meliputi rumus dan beberapa contoh soal untuk meningkatkan pemahamanmu.

—

Halo, teman-teman! Di artikel sebelumnya, kamu sudah belajar mengenai pengertian serta rumus barisan dan deret aritmatika, ya. Hayoo, ada yang masih ingat, apa bedanya barisan dengan deret aritmatika?

Yaps! Betul banget! Barisan aritmatika adalah barisan bilangan yang mempunyai beda (selisih) yang tetap di antara suku-sukunya yang saling berdekatan, sedangkan deret aritmatika adalah jumlah suku ke-n pertama pada barisan aritmatika.

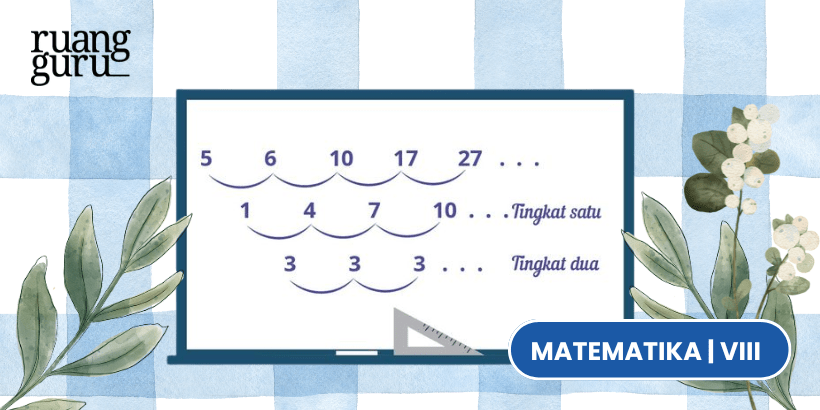
Nah, di materi barisan aritmatika yang sudah kamu pelajari sebelumnya, nilai beda yang tetap antara dua suku yang saling berurutan, bisa langsung kamu temukan. Contohnya, seperti gambar di atas, nih. Kita bisa langsung tahu kalau barisan aritmatika tersebut memiliki nilai beda tetap, yaitu 3.

Lalu, gimana nih kalau kamu menemukan soal barisan aritmatika yang nilai bedanya nggak tetap, alias nggak sama? Contohnya, kayak barisan aritmatika di bawah ini.

1, 5, 12, 22, 35, …

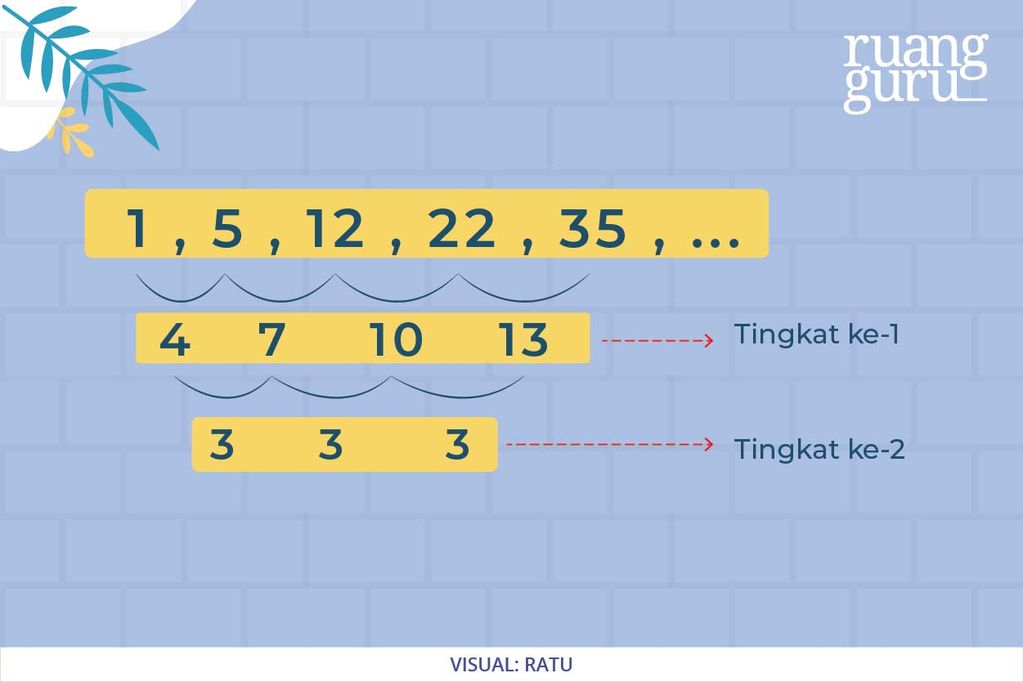
Nah, kalau kamu perhatikan, pada barisan aritmatika tersebut, beda antara suku pertama (U₁) dengan suku ke-2 (U₂) adalah 4. Tapi, beda antara suku ke-2 (U₂) dengan suku ke-3 (U₃) adalah 7. Begitupun dengan beda antara dua suku-suku berikutnya yang ternyata nggak sama. Tandanya, nilai beda tetapnya belum langsung bisa kita temukan pada barisan tersebut.

Tapi, coba kamu perhatikan hasil dari selisih suku-suku yang saling berdekatannya, deh. Kalau kita anggap selisih suku-suku itu sebagai barisan baru, lalu kita cari kembali nilai bedanya, ternyata suku-suku baru tersebut memiliki nilai beda yang sama atau tetap, ya, yaitu 3 (lihat gambar di bawah).

Baca Juga: Cara Mencari Rumus Pola Bilangan berdasarkan Jenis-Jenis dan Contohnya

Nah, jika barisan pertama kita anggap sebagai barisan tingkat satu, lalu suku-suku baru yang merupakan hasil selisih barisan sebelumnya kita anggap sebagai barisan tingkat dua, maka, artinya, nilai beda tetap dari barisan aritmatika tersebut baru bisa kita temukan di tingkat keduanya, ya.

Pengertian Barisan Aritmatika Bertingkat

Nah, barisan aritmatika yang nilai beda tetapnya nggak langsung ditemukan di tingkat pertamanya, sehingga kita harus mencari beda (selisih) yang bernilai tetap di tingkat-tingkat berikutnya, bisa kita sebut dengan barisan aritmatika bertingkat.

Kalau nilai beda tetapnya langsung bisa ditemukan di barisan tingkat pertamanya, kita bisa menyebutnya dengan barisan aritmatika bertingkat satu. Kalau nilai beda tetapnya ditemukan di barisan tingkat keduanya, kita bisa sebut dengan barisan aritmatika bertingkat dua. Kalau nilai beda tetapnya ditemukan di barisan tingkat ketiganya, kita bisa sebut dengan barisan aritmatika bertingkat tiga, begitupun seterusnya.

Jadi, tingkatan pada barisan aritmatika bertingkat itu sebenarnya banyak sekali, ya. Bisa sampai bertingkat lima, enam, tujuh, dan seterusnya.

Tapi, kamu nggak perlu khawatir nih, untuk materi barisan aritmatika bertingkat yang ada di SMP ini, biasanya, hanya sampai di tingkatan ke-2 atau ke-3 saja, ya.

Paham ya dengan konsep barisan aritmatika bertingkat? Lalu, gimana sih cara mencari suku ke-n (U_n) pada barisan aritmatika bertingkat itu?

Baca Juga: Belajar Konsep Sistem Koordinat Kartesius dan Cara Membuat Grafiknya, Yuk!

Rumus Barisan Aritmatika Bertingkat Dua

Untuk mencari U_n pada barisan aritmatika bertingkat satu, rumusnya sama saja ya dengan rumus barisan aritmatika yang sudah kamu pelajari sebelumnya, yaitu U_n = a + (n-1)b. Nah, untuk mencari U_n pada barisan aritmatika bertingkat dua dan tiga, kamu bisa menggunakan rumus di bawah ini, nih.

Sekarang, coba kita cari pola barisan bertingkat duanya ya dari rumus tersebut.

• Kalau kita masukkan n = 1 ke dalam U_n = an² + bn + c, maka diperoleh suku pertama, yaitu:
  U_n = an² + bn + c
  U₁ = a(1)² + b(1) +c
  U₁ = a + b + c  

• Kalau kita masukkan n = 2 ke dalam U_n = an² + bn + c, maka diperoleh suku kedua, yaitu:
  U_n = an² + bn + c
  U₂ = a(2)² + b(2) +c
  U₂ = 4a + 2b + c

• Kalau kita masukkan n = 3 ke dalam U_n = an² + bn + c, maka diperoleh suku ketiga, yaitu:
  U_n = an² + bn + c
  U₃ = a(3)² + b(3) +c
  U₃ = 9a + 3b + c

• Kalau kita masukkan n = 4 ke dalam U_n = an² + bn + c, maka diperoleh suku keempat, yaitu:
  U_n = an² + bn + c
  U₄ = a(4)² + b(4) +c
  U₄ = 16a + 4b + c

Sehingga, akan diperoleh barisan aritmatika sebagai berikut:

Kemudian, kalau kita cari beda (selisih) dari suku-suku tersebut, maka diperoleh:

• Beda suku pertama (U₁) dengan suku kedua (U₂)

b = U₂ – U₁ = (4a + 2b + c) – (a + b + c)

b = 4a – a + 2b – b + c – c

b = 3a + b

• Beda suku kedua (U₂) dengan suku ketiga (U₃)

b = U₃ – U₂ = (9a + 3b + c) – (4a + 2b + c)

b = 9a – 4a + 3b – 2b + c – c

b = 5a + b

• Beda suku ketiga (U₃) dengan suku keempat (U₄)

b = U₄ – U₃ = (16a + 4b + c) – (9a + 3b + c)

b = 16a – 9a + 4b – 3b + c – c

b = 7a + b

Sehingga, beda antara suku-suku yang saling berdekatan pada barisan aritmatika tersebut adalah:

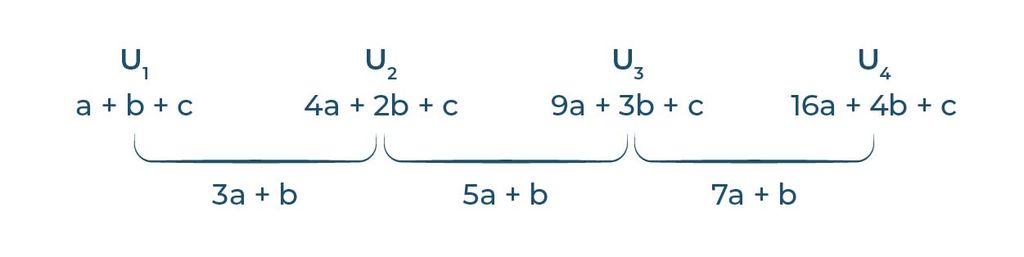
(gambar 1)

Nah, karena kita mencari pola barisan aritmatika bertingkat dua menggunakan rumus barisan aritmatika bertingkat dua, maka kamu bisa lihat ya kalau beda antara suku-suku tersebut belum tetap atau sama. Jadi, kita anggap 3a + b, 5a + b, dan 7a + b sebagai suku-suku baru di tingkat pertama. Lalu, kita cari lagi selisih antara suku-suku baru tersebut untuk mendapatkan beda yang tetap di tingkat kedua.

• Beda suku pertama di tingkat pertama (U₁*) dengan suku kedua di tingkat pertama (U₂*)

b = U₂* – U₁* = 5a + b – (3a + b)

b = 5a – 3a + b – b = 2a

• Beda suku kedua di tingkat pertama (U₂*) dengan suku ketiga di tingkat pertama (U₃*)

b = U₃* – U₂* = 7a + b – (5a + b)

b = 7a – 5a + b – b = 2a

Sehingga, beda antara suku-suku baru di tingkat 1 yang saling berdekatan pada barisan aritmatika tersebut adalah:

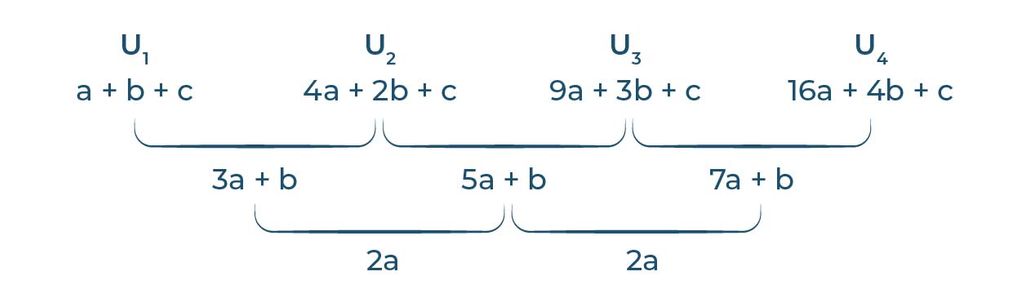
(gambar 2)

Nah, sekarang kamu bisa lihat nih, di tingkat kedua, kita sudah bisa mendapatkan beda yang tetap, yaitu 2a.

Baca Juga: Cara Menyelesaikan Persamaan Linear Dua Variabel (SPLDV)

Lalu, buat apa sih kita mencari pola barisan aritmatika bertingkat dua, seperti gambar di atas? Tujuannya itu, memudahkan kamu untuk mendapatkan nilai a, b, dan c yang terdapat pada rumus barisan aritmatika bertingkat dua (U_n = an² + bn + c).

Oke, supaya kamu semakin paham, kita masuk ke contoh soal, deh.

 

Contoh Soal Barisan Aritmatika Bertingkat Dua

Tentukan suku ke-7 dari barisan aritmatika bertingkat 5, 6, 9, 14, …

Pembahasan:

Diketahui, U₁ = 5, U₂ = 6, U₃ = 9, dan U₄ = 14.

• Beda antara U₁ dengan U₂

b = U₂ – U₁ = 6 – 5 = 1

• Beda antara U₂ dengan U₃

b = U₃ – U₂ = 9 – 6 = 3

• Beda antara U₃ dengan U₄

b = U₄ – U₃ = 14 – 9 = 5

Sehingga, diperoleh pola barisan aritmatika sebagai berikut:

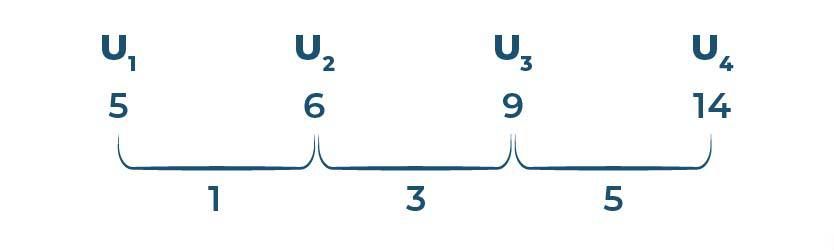
Kemudian, karena bedanya belum tetap (sama), kita anggap 1, 3, dan 5 sebagai suku-suku baru di tingkat pertama, dan kita cari selisih antara suku-suku baru tersebut.

• Beda antara U₁* dengan U₂*

b = U₂* – U₁* = 3 – 1 = 2

• Beda antara U₂* dengan U₃*

b = U₃* – U₂* = 5 – 3 = 2

Sehingga, diperoleh pola barisan aritmatika bertingkat dua sebagai berikut:

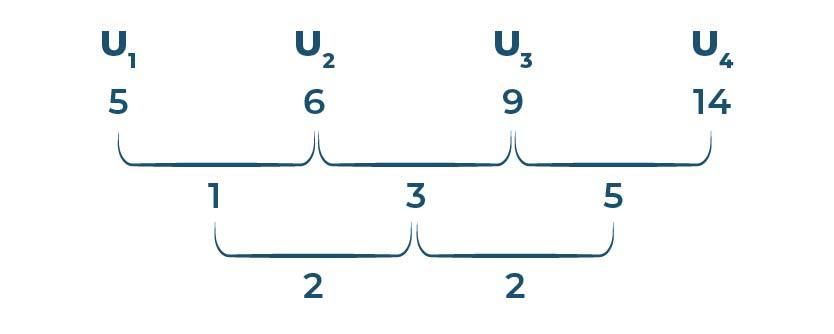
Nah, kamu masih ingat kan dengan rumus barisan aritmatika bertingkat dua? Yap! Betul! U_n = an² + bn + c. Seperti yang sudah dijelaskan sebelumnya, untuk mencari nilai a, b, dan c pada rumus tersebut, kita bisa gunakan pola barisan aritmatika bertingkat dua yang sudah kita cari di atas (gambar 2).

Kita samakan pola barisan aritmatika pada gambar 2 dengan pola barisan aritmatika yang sudah kita peroleh dari soal.

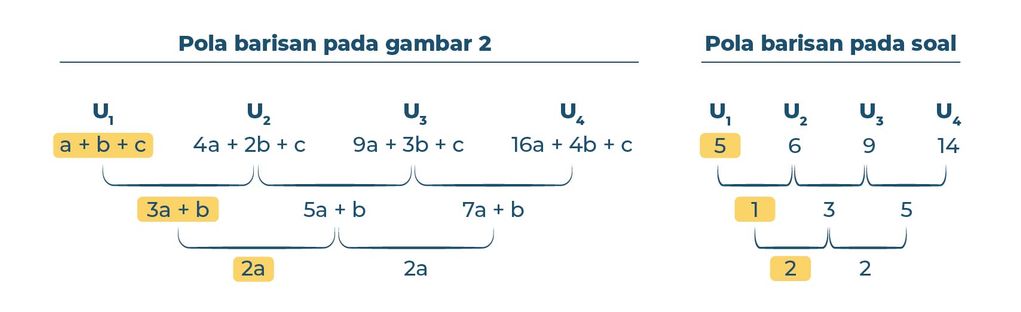
Kalau kita lihat polanya, 2a nilainya sama dengan 2. Berarti, a + b + c nilainya sama dengan 5 dan 3a + b nilainya sama dengan 1. Sehingga,

• 2a = 2
  a = 1
• 3a + b = 1
  3(1) + b = 1
  b = 1 – 3
  b = -2
• a + b + c = 5
  1 – 2 + c = 5
  c = 5 – 1 + 2
  c = 6

Setelah kita dapat nilai a, b, dan c, kita masukkan nilainya ke dalam rumus barisan aritmatika bertingkat dua:

U_n = an² + bn + c

U_n = n² – 2n + 6

Kemudian, kita diminta mencari suku ke-7, berarti U₇ dengan n = 7. Jadi, kita masukkan saja nilai n = 7 ke dalam rumus U_n = n² – 2n + 6.

U₇ = 7² – (2)(7) + 6 = 49 – 14 + 6 = 41

Sampai sini paham ya, teman-teman? Kita lanjut ke rumus barisan aritmatika bertingkat tiga, ya.

Baca Juga: Cara Mencari Kemiringan (Gradien) pada Garis Lurus

Rumus Barisan Aritmatika Bertingkat Tiga

 

Langkah-langkahnya sama nih dengan yang sudah kita kerjakan sebelumnya. Kita cari dulu pola barisan aritmatika bertingkat tiganya ya dari rumus di atas.

• Kalau kita masukkan n = 1 ke dalam U_n = an³ + bn² + cn + d, maka diperoleh suku pertama, yaitu:
  U_n = an³ + bn² + cn + d
  U₁ = a(1)³ + b(1)² + c(1) + d
  U₁ = a + b + c + d  

• Kalau kita masukkan n = 2 ke dalam U_n = an³ + bn² + cn + d, maka diperoleh suku kedua, yaitu:
  U_n = an³ + bn² + cn + d
  U₂ = a(2)³ + b(2)² + c(2) + d
  U₂ = 8a + 4b + 2c + d

• Kalau kita masukkan n = 3 ke dalam U_n = an³ + bn² + cn + d, maka diperoleh suku ketiga, yaitu:
  U_n = an³ + bn² + cn + d
  U₃ = a(3)³ + b(3)² + c(3) + d
  U₃ = 27a + 9b + 3c + d

• Kalau kita masukkan n = 4 ke dalam U_n = an³ + bn² + cn + d, maka diperoleh suku keempat, yaitu:
  U_n = an³ + bn² + cn + d
  U₄ = a(4)³ + b(4)² + c(4) + d
  U₄ = 64a + 16b + 4c + d

• Kalau kita masukkan n = 5 ke dalam U_n = an³ + bn² + cn + d, maka diperoleh suku kelima, yaitu:
  U_n = an³ + bn2 + cn + d
  U₅ = a(5)³ + b(5)2 + c(5) + d
  U₅ = 125a + 25b + 5c + d

Kemudian, kalau kita cari beda (selisih) dari suku-suku tersebut, maka diperoleh:

• Beda suku pertama (U₁) dengan suku kedua (U₂)

b = U₂ – U₁ = (8a + 4b + 2c + d) – (a + b + c + d)

b = 8a – a + 4b – b + 2c – c + d – d

b = 7a + 3b + c

• Beda suku kedua (U₂) dengan suku ketiga (U₃)

b = U₃ – U₂ = (27a + 9b + 3c + d) – (8a + 4b + 2c + d)

b = 27a – 8a + 9b – 4b + 3c – 2c + d – d

b = 19a + 5b + c

• Beda suku ketiga (U₃) dengan suku keempat (U₄)

b = U₄ – U₃ = (64a + 16b + 4c + d) – (27a + 9b + 3c + d)

b = 64a – 27a + 16b – 9b + 4c – 3c + d – d

b = 37a + 7b + c

• Beda suku ketiga (U₄) dengan suku keempat (U₅)

b = U₅ – U₄ = (125a + 25b + 5c + d) – (64a + 16b + 4c + d)

b = 125a – 64a + 25b – 16b + 4c – 3c + d – d

b = 61a + 9b + c

Sehingga, beda antara suku-suku yang saling berdekatan pada barisan aritmatika tersebut adalah:

(gambar 3)

Karena beda antara suku-sukunya belum sama, kita anggap 7a + 3b + c, 19a + 5b + c, 37a + 7b + c, dan 61a + 9b + c sebagai suku-suku baru di tingkat pertama. Lalu, kita cari lagi selisih antara suku-suku baru tersebut untuk mendapatkan beda yang tetap.

• Beda suku pertama di tingkat pertama (U₁*) dengan suku kedua di tingkat pertama (U₂*)

b = U₂* – U₁* = 19a + 5b + c – (7a + 3b + c)

b = 19a – 7a + 5b – 3b + c – c

b = 12a + 2b

• Beda suku kedua di tingkat pertama (U₂*) dengan suku ketiga di tingkat pertama (U₃*)

b = U₃* – U₂* = 37a + 7b + c – (19a + 5b + c)

b = 37a – 19a + 7b – 5b + c – c

b = 18a + 2b

• Beda suku kedua di tingkat pertama (U₃*) dengan suku ketiga di tingkat pertama (U₄*)

b = U₄* – U₃* = 71a + 9b + c – (37a + 7b + c)

b = 61a – 37a + 9b – 7b + c – c

b = 24a + 2b

Sehingga, beda antara suku-suku baru di tingkat 1 yang saling berdekatan pada barisan aritmatika tersebut adalah:

(gambar 4)

Baca Juga: Yuk, Kita Belajar Cara Menentukan Persamaan Garis Lurus!

Kita masih belum menemukan nilai beda yang tetap nih, oleh karena itu, kita anggap 12a + 2b, 18a + 2b, dan 24a + 2b sebagai suku-suku baru di tingkat kedua. Lalu, kita cari lagi selisih suku-suku baru tersebut agar mendapat nilai beda yang tetap.

• Beda suku pertama di tingkat pertama (U₁**) dengan suku kedua di tingkat pertama (U₂**)

b = U₂** – U₁** = 18a + 2b – (12a + 2b)

b = 18a – 12a + 2b – 2b

b = 6a

• Beda suku kedua di tingkat pertama (U₂**) dengan suku ketiga di tingkat pertama (U₃**)

b = U₃** – U₂** = 24a + 2b – (18a + 2b)

b = 24a – 18a + 2b – 2b

b = 6a

Sehingga, beda antara suku-suku baru di tingkat 2 yang saling berdekatan pada barisan aritmatika tersebut adalah:

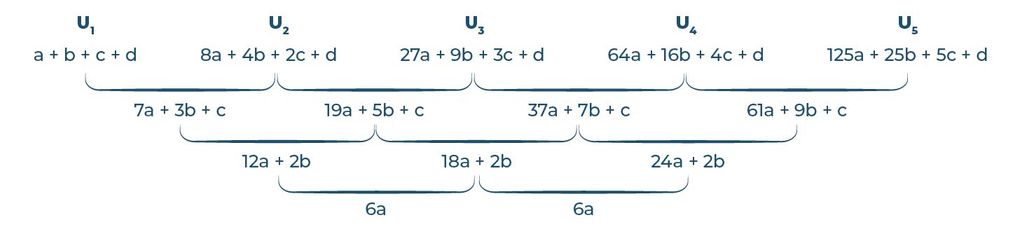
(gambar 5)

Sekarang, kamu bisa lihat kan, di tingkat kedua, kita sudah bisa mendapatkan beda yang tetap, yaitu 6a.

Sama seperti pola pada barisan aritmatika bertingkat dua, pola barisan aritmatika bertingkat tiga tersebut akan membantu kita untuk mencari nilai a, b, c, dan d pada rumus barisan aritmatika bertingkat tiga (U_n = an³ + bn² + cn + d).

Oke, seperti biasa, supaya kamu nggak bingung, yuk kita kerjakan soal di bawah ini sama-sama, ya!

 

Contoh Soal Barisan Aritmatika Bertingkat Tiga

Tentukanlah suku ke-10 dari barisan aritmatika bertingkat 1, 3, 11, 31, 69, …

Pembahasan:

Diketahui, U₁ = 1, U₂ = 3, U₃ = 11, U₄ = 31, dan U₅ = 69.

• Beda antara U₁ dengan U₂

b = U₂ – U₁ = 3 – 1 = 2

• Beda antara U₂ dengan U₃

b = U₃ – U₂ = 11 – 3 = 8

• Beda antara U₃ dengan U₄

b = U₄ – U₃ = 31 – 11 = 20

• Beda antara U₄ dengan U₅

b = U₅ – U₄ = 69 – 31 = 38

Sehingga, diperoleh pola barisan aritmatika sebagai berikut:

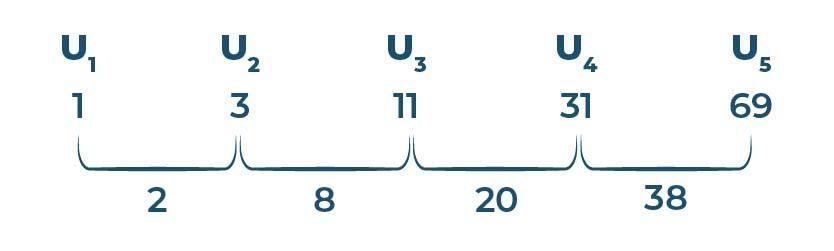
Kemudian, karena bedanya belum tetap (sama), kita anggap 2, 8, 20, dan 38 sebagai suku-suku baru di tingkat pertama, dan kita cari selisih antara suku-suku baru tersebut.

• Beda antara U₁* dengan U₂*

b = U₂* – U₁* = 8 – 2 = 6

• Beda antara U₂* dengan U₃*

b = U₃* – U₂* = 20 – 8 = 12

• Beda antara U₃* dengan U₄*

b = U₄* – U₃* = 38 – 20 = 18

Sehingga, diperoleh pola barisan aritmatika bertingkat dua sebagai berikut:

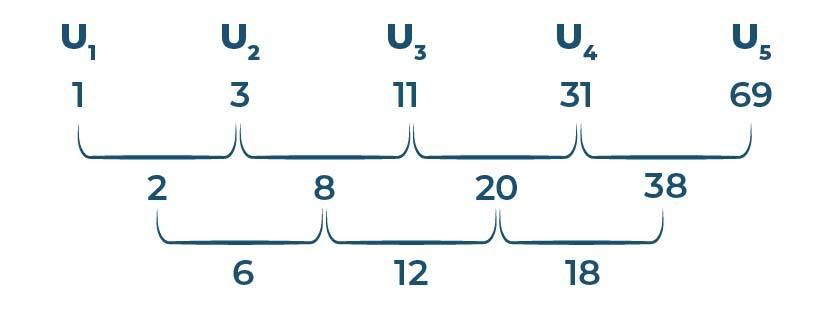
Baca Juga: Pengertian Relasi dan Fungsi serta Cara Menyatakannya

Nilai bedanya belum sama, kita anggap lagi 6, 12, dan 18 sebagai suku-suku baru di tingkat kedua, dan kita cari selisihnya kembali.

• Beda antara U₁** dengan U₂**

b = U₂** – U₁** = 12 – 6 = 6

• Beda antara U₂** dengan U₃**

b = U₃** – U₂** = 18 – 12 = 6

Sehingga, diperoleh pola barisan aritmatika bertingkat tiga sebagai berikut:

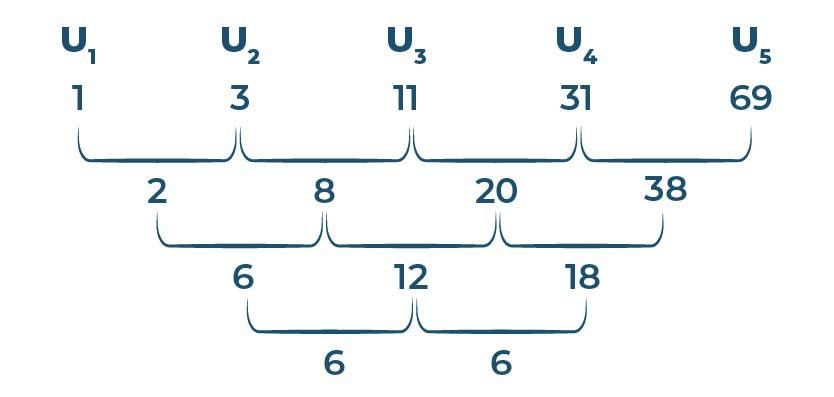
Rumus barisan aritmatika bertingkat tiga, yaitu U_n = an³ + bn² + cn + d. Seperti yang sudah dijelaskan sebelumnya, untuk mencari nilai a, b, c, dan d pada rumus tersebut, kita bisa gunakan pola barisan aritmatika bertingkat tiga yang sudah kita cari di atas (gambar 5).

Selanjutnya, kita samakan pola barisan aritmatika pada gambar 5 dengan pola barisan aritmatika yang sudah kita peroleh dari soal.

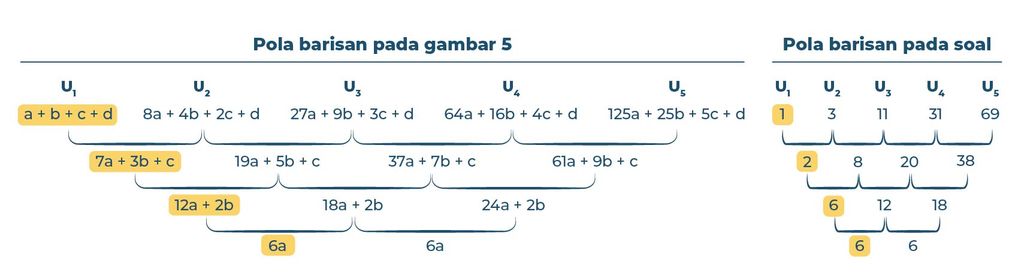
Kalau kita lihat polanya, 6a nilainya sama dengan 6. Berarti, a + b + c nilainya sama dengan 1, 7a + 3b + c nilainya sama dengan 2, dan 12a + 2b nilainya sama dengan 6. Sehingga,

• 6a = 6
  a = 1
• 12a + 2b = 6
  12(1) + 2b = 6
  2b = 6 – 12
  2b = -6
  b = -6/2
  b = -3
• 7a + 3b + c = 2
  7(1) + 3(-3) + c = 2
  7 – 9 + c = 2
  c = 2 – 7 + 9
  c = 4
• a + b + c + d = 1
  1 – 3 + 4 + d = 1
  2 + d = 1
  d = 1 – 2
  d = -1

Setelah kita dapat nilai a, b, c, dan d, kita masukkan nilainya ke dalam rumus barisan aritmatika bertingkat tiga:

U_n = an³ + bn² + cn + d

U_n = n³ – 3n² + 4n – 1

Kemudian, kita diminta mencari suku ke-10, berarti U10 dengan n = 10. Jadi, kita masukkan saja nilai n = 10 ke dalam rumus U_n = n³ – 3n² + 4n – 1.

U₁₀ = (10)³ – (3)(10)² + 4(10) – 1

U₁₀ = 1000 – 300 + 40 – 1 = 739

Baca Juga: Mengenal Statistika dan Diagram Penyajian Data, Kuy!

Oke, selesai sudah materi kita kali ini, ya. Wah, untuk materi barisan aritmatika bertingkat ini, sepintas memang cukup sulit, ya. Rumus untuk mencari suku barisan bertingkat juga berbeda pada tiap tingkatannya. Tapi, kamu bisa menaklukkan materi ini dengan banyak berlatih soal, lho. Download aja aplikasi Ruangguru dan asah kemampuanmu dengan berlatih berbagai macam tipe soal di ruangbelajar!

Referensi:

As’ari AR, Tohir M, dkk. (2017) Matematika Kelas VIII SMP/MTs. Edisi Revisi. Jakarta: Kementerian Pendidikan dan Kebudayaan

 

Artikel diperbarui pada 12 Oktober 2022.