Fisika Kelas 10 | 3 Metode Penjumlahan Vektor

Pada artikel Fisika kelas X kali ini, kamu akan mengetahui cara menjumlahkan vektor menggunakan tiga metode, yaitu metode grafis, analisis, dan uraian.

—

Siapa di antara kamu yang suka lari? Eits! Bukan lari dari masalah kehidupan loh, ya hehe. Tapi, olahraga lari, jogging gitu misalnya. Kamu tahu nggak nih, kalau jogging itu banyak manfaatnya, lho! Mulai dari meningkatkan kekebalan tubuh, fisik menjadi lebih fit dan segar, sampai menghilangkan stres. Wah, boleh juga tuh! Hitung-hitung, menghilangkan penat akibat banyaknya tugas di sekolah atau menyegarkan pikiran sebelum menghadapi ujian. 

Ngomong-ngomong masalah jogging, Rogu juga rutin melakukan jogging setiap Minggu pagi, lho. Biasanya, Rogu jogging di sekitar komplek tempat ia tinggal. Nah, berikut ini merupakan gambaran rute jogging yang biasa Rogu lewati.

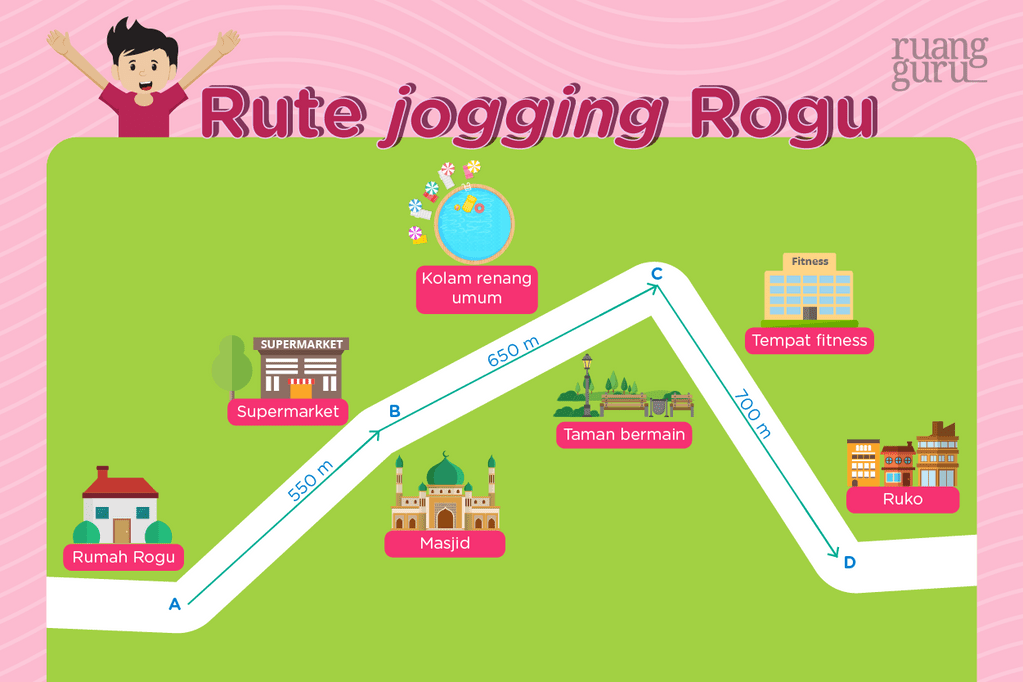
Kira-kira nih, kamu bisa nggak menghitung berapa jarak yang ditempuh Rogu dari titik A ke titik D? Wah, kalau itu sih caranya mudah sekali, ya. Kita hanya tinggal menjumlahkan jarak dari titik AB ke titik BC, lalu ke titik CD. Sehingga, AB + BC + CD = 550 m + 650 m + 700 m = 1.900 m. Simpel banget, kan? Tapi, bagaimana dengan perpindahan Rogu dari titik A ke titik D?

Nah, jika kamu ingat, perpindahan itu termasuk besaran vektor, Squad. Perpindahan ditentukan oleh kedudukan awal dan kedudukan akhir, serta dapat bertanda positif maupun negatif, bergantung pada arah perpindahannya. Gambar rute jogging Rogu di atas bisa kita analogikan sebagai vektor nih, dengan memisalkan F₁ merupakan vektor di titik AB, F₂ merupakan vektor di titik BC, dan F₃ merupakan vektor di titik CD.

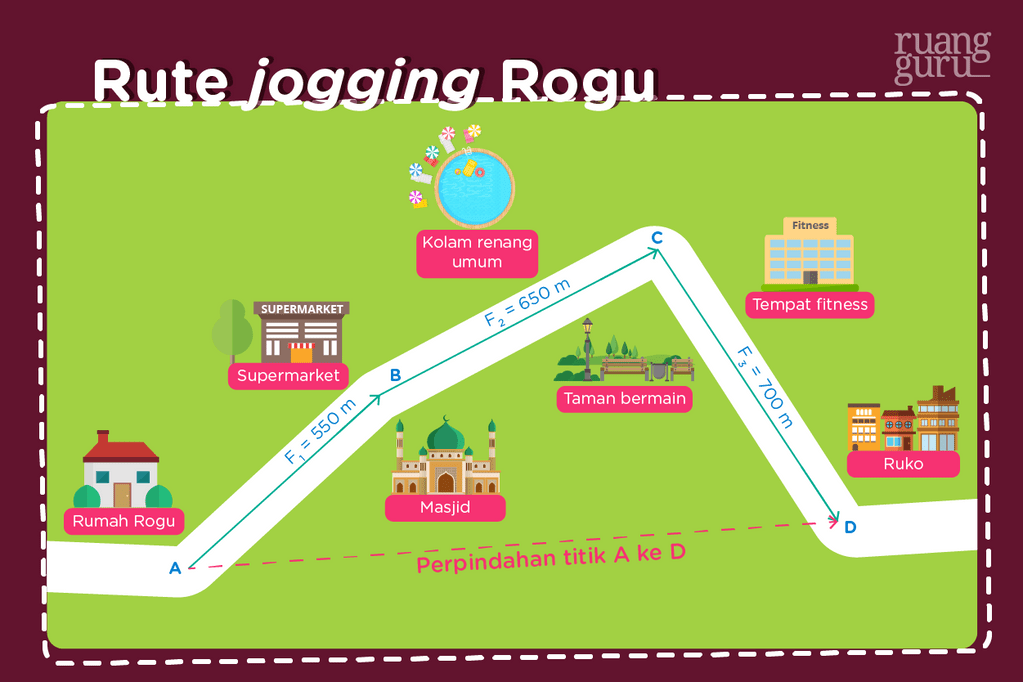
Kemudian, perpindahan dari titik A ke titik D dapat ditentukan dengan mencari besar resultan vektornya saja. Apa itu resultan vektor? Resultan vektor adalah hasil dari penjumlahan dua atau lebih vektor. Terdapat beberapa metode yang bisa kita gunakan untuk mencari resultan vektor nih, di antaranya metode grafis, metode analisis vektor, atau metode uraian. So, kalau kamu mau tahu metode apa yang tepat untuk mencari besar perpindahan Rogu dari titik A ke titik D, yuk simak baik-baik artikel ini!

1. Metode grafis

Metode yang pertama adalah metode grafis. Metode grafis adalah metode yang digunakan untuk menentukan besar resultan vektor dengan cara mengukurnya. Panjang resultan vektor dapat diukur menggunakan mistar (penggaris), sedangkan besar sudut vektor (arah vektor) diukur menggunakan busur derajat. Perlu kamu ingat, pengukuran besar resultan vektor menggunakan metode grafis harus berdasarkan skala dan besar sudut yang tepat, ya.

Nah, jika kamu menyimak cerita Rogu di atas, metode grafis ini merupakan metode yang tepat untuk mencari besar perpindahan Rogu dari titik A ke titik D. Langkah pertama yang bisa kamu lakukan adalah menetapkan skala dari masing-masing besaran vektor. Ingat! skala yang kita tentukan harus tepat dan juga sesuai ya, Squad.

Berdasarkan cerita Rogu, besar vektor F₁= 550 m, besar vektor F₂= 650 m, dan besar vektor F₃= 700 m. Misalkan, untuk ketiga vektor, kita menetapkan skala 100 m = 1 cm. Artinya, setiap panjang 100 m kita gambar dengan 1 cm di kertas. Jadi, vektor F₁ dapat digambar sepanjang 5,5 cm, vektor F₂ digambar sepanjang 6,5 cm, dan vektor F₃ digambar sepanjang 7 cm.

Paham sampai di sini? Kita lanjut, ya.

Kemudian, langkah kedua adalah menggambar besar dan arah masing-masing vektor seperti pada gambar di bawah ini. Panjang vektor R = F_¹+F₂+F₃ dapat dihitung menggunakan penggaris. Sementara itu, sudut arah vektor R dihitung menggunakan busur derajat.

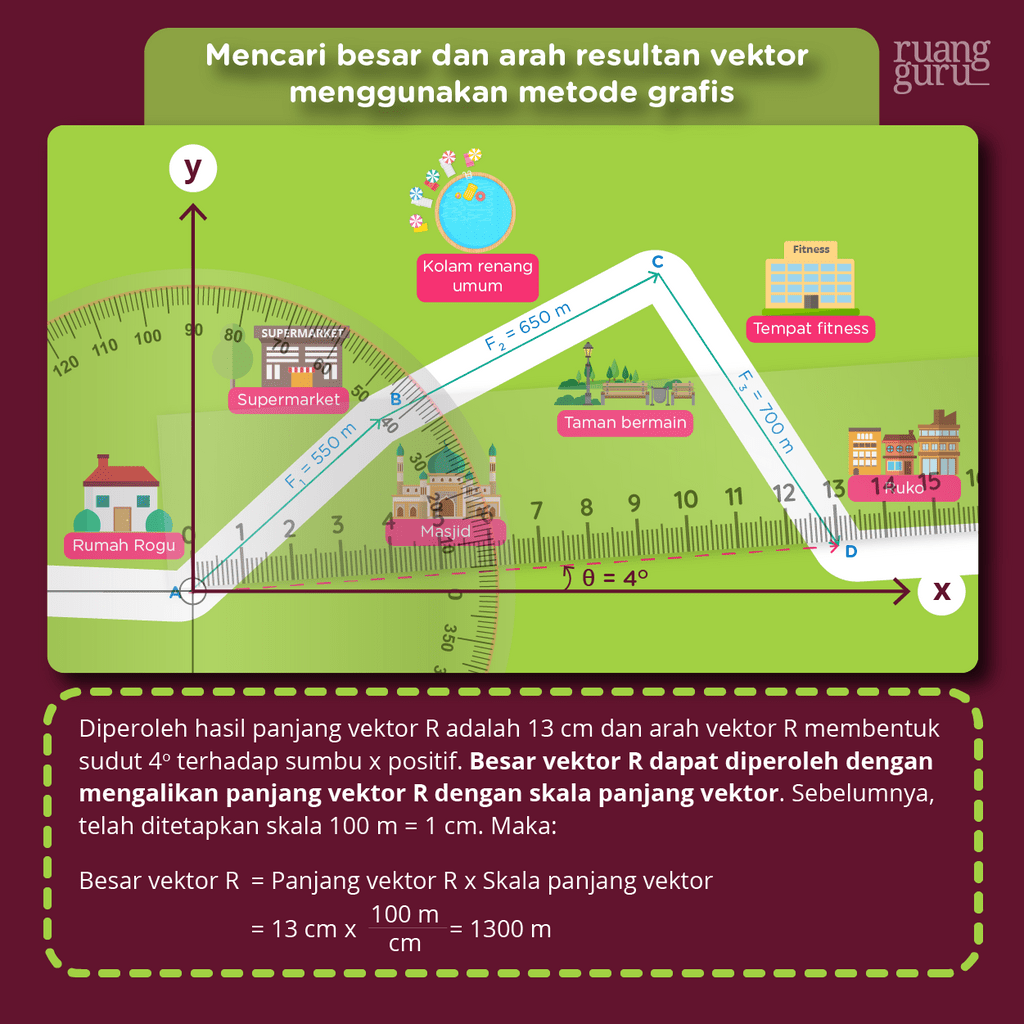
Sebelumnya, kita sudah tahu ya kalau untuk mencari perpindahan dari satu titik ke titik lain kita hanya tinggal menghitung besar resultan vektornya saja, jadi sudah dapat kita ketahui nih kalau perpindahan Rogu dari titik A ke titik D adalah sebesar 1.300 m.

Jelas ya? Bagi yang belum paham, tulis saja pertanyaanmu di kolom komentar, oke?

Oh iya, penggunaan metode grafis dalam menghitung jumlah dua atau lebih vektor ternyata memiliki kelemahan lho, yaitu dapat menimbulkan kesalahan sistematis. Nah, untuk menghindari kesalahan tersebut, kita dapat menggunakan metode yang akan kita bahas selanjutnya, yaitu metode analitis.

2. Metode analitis

Metode analitis adalah metode yang digunakan untuk menentukan besar resultan vektor secara matematis dengan menggunakan rumus. Adapun rumus yang digunakan merupakan rumus kosinus (cos) untuk menentukan besar resultan vektor dan rumus sinus (sin) untuk menentukan arah resultan vektor.

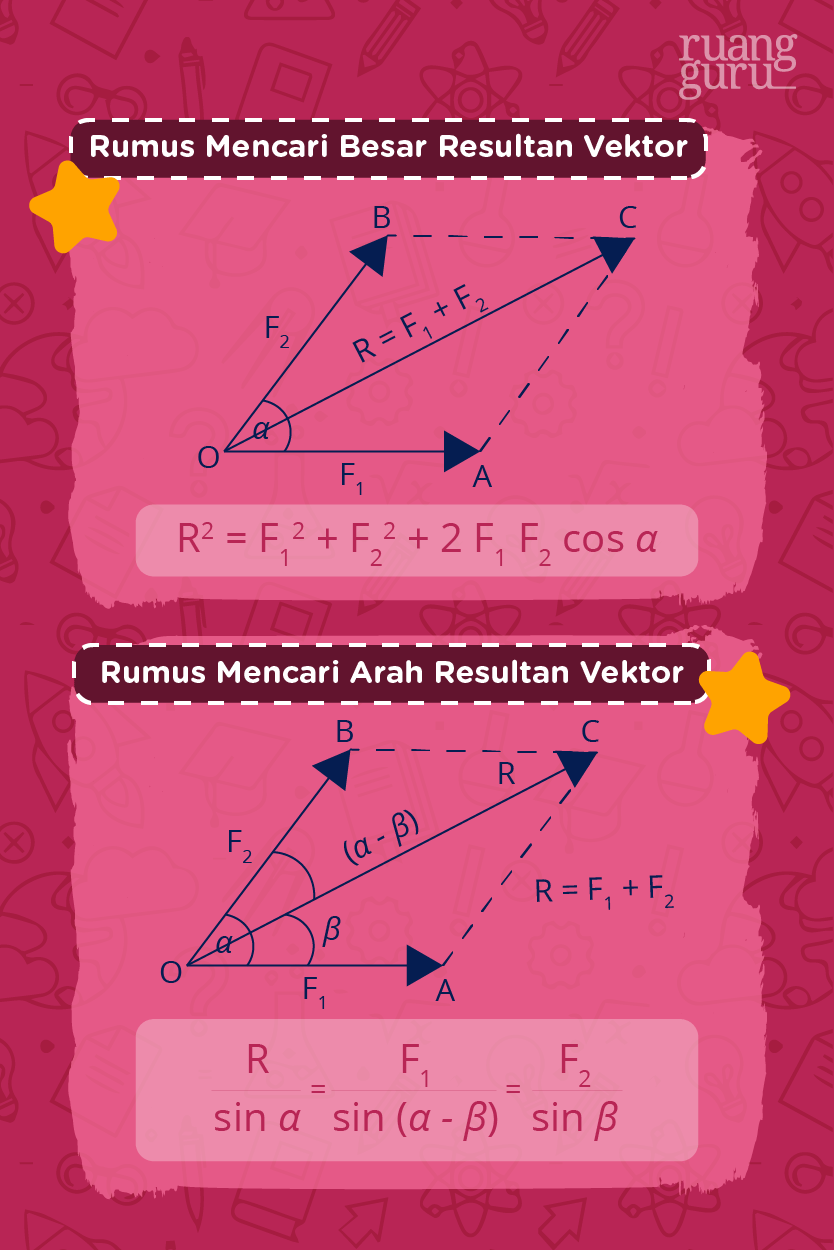
Sekarang, supaya kamu lebih mudah untuk memahami cara mencari besar dan arah resultan vektor menggunakan metode ini, yuk, langsung saja kita simak contoh soal berikut ini.

Contoh soal

Hitunglah besar dan arah vektor resultannya terhadap sumbu x positif!

Penyelesaian:

a. Besar resultan vektor

 b. Arah resultan vektor

Jadi, besar resultan vektornya adalah  dan arah resultan vektornya adalah 22,3^o terhadap sumbu x positif. Gimana, mudah, kan? Oke, selanjutnya, kita masuk ke metode penjumlahan vektor yang terakhir, nih. Apakah itu? Yap! Metode uraian.

3. Metode uraian

Metode penjumlahan vektor yang terakhir adalah metode uraian. Pada materi sebelumnya, kamu telah mempelajari cara mencari komponen-komponen dari suatu vektor kan, Squad. Nah, pada metode uraian ini, sebelum kita mencari besar resultan vektor, kita uraikan terlebih dahulu vektor-vektor tersebut menjadi komponen vektor pada sumbu x dan komponen vektor pada sumbu y di koordinat kartesius.

Kamu masih ingat kan cara mencari komponen vektor pada sumbu x dan y? Hayo, bagi yang sudah lupa, dipahami lagi ya materi sebelumnya.

Setelah kita menguraikan vektor-vektor tersebut menjadi komponen vektor, barulah kita bisa mencari besar resultan vektornya, yaitu dengan menggunakan rumus 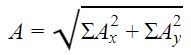  dan arah resultan vektornya dengan rumus 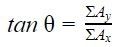. Nah,  ini artinya jumlah komponen-komponen vektor pada sumbu x dan  artinya jumlah komponen-komponen vektor pada sumbu y.

Perlu kamu perhatikan, besar suatu vektor akan selalu bernilai positif. Selain itu, dalam menentukan arah vektor, kita harus memperhatikan tanda A_x dan A_y yang nantinya akan menentukan kuadran dari vektor dalam sistem koordinat seperti pada tabel berikut ini:

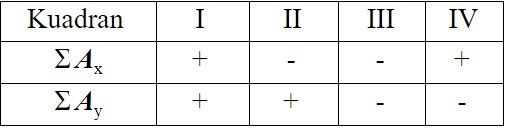
Bingung? Tenang, nggak usah bingung-bingung, kita langsung coba kerjakan contoh soal di bawah ini saja, yuk! Let’s go!

Contoh Soal

Apabila F₁ = 2 N, F₂ = 10 N, dan F₃ = 6 N, maka tentukan resultan dari ketiga vektor tersebut!

Pembahasan:

Hal pertama yang bisa kita lakukan untuk mengerjakan soal di atas adalah dengan menguraikan vektor F₁, F₂, dan F₃ terhadap sumbu x dan sumbu y.

Pada sumbu x:

➔F_1x → -F_1x = -2 N (tanda negatif menandakan arah vektor ke kiri).

➔F_2x = F₂ sin θ → F_2x = (10) sin 53°= (10)(0,8) = 8 N (tanda positif menandakan arah vektor ke kanan).

➔F_3x = 0 N (angka nol (0) menandakan F₃ tidak memiliki proyeksi vektor/komponen vektor pada sumbu x karena F₃ tegak lurus terhadap sumbu x).

Jadi, ΣF_x = F_1x + F_2x + F_3x = -2 + 8 + 0 = 6 N

Pada sumbu y:

➔F_1y = 0 N (angka nol (0) menandakan F₁ tidak memiliki proyeksi vektor/komponen vektor pada sumbu y karena F₁ tegak lurus terhadap sumbu y).

➔F_2y = -F₂ cos θ = -(10) cos 53° = -(10)(0,6) = -6 N (tanda negatif menandakan arah vektor ke bawah).

➔F_3y = 6 N (tanda positif menandakan arah vektor ke atas).

Jadi, Σ_Fy = F_1y + F_2y + F_3y = 0 + 6 – 6 = 0 N

Selanjutnya, setelah kita mengetahui komponen-komponen dari ketiga vektor di atas terhadap sumbu x dan y, maka kita dapat mencari resultan dari ketiga vektor tersebut.

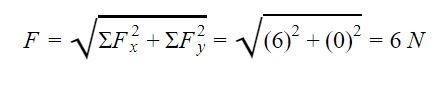
Jadi, resultan dari vektor F₁, F₂, dan F₃ adalah 6 N. Gimana? Ternyata nggak sesulit yang kamu kira, kan?

Oke, setelah kamu memahami ketiga metode penjumlahan vektor di atas, menurutmu, metode mana yang lebih mudah? Eits! Tapi ingat, jangan mentang-mentang kamu sreg dengan satu metode, terus metode yang lainnya tidak kamu pahami, deh. Kamu juga harus paham ketiga-tiganya, Squad. Siapa tahu keluar di ujian nanti.

Oh iya, bagi yang masih belum paham dengan materi kali ini, atau ingin bertanya lebih lanjut pada ahlinya, kamu bisa lho dengan menggunakan aplikasi Ruangguru melalui fitur ruanglesonline. Di sana, kamu akan dibantu oleh para tutor yang handal untuk membahas soal dan memahami pelajaran via live chat. Belajar kamu jadi semakin praktis, deh!