Latihan Soal UNBK SMA Matematika IPA Tahun 2020

Artikel ini berisi kumpulan soal sma matematika ipa yang dapat digunakan untuk ajang latihan menjelang UNBK 2020.

—

Topik: Relasi dan Fungsi (NEW)
Subtopik: Aljabar Fungsi I
Level Kognitif: LOTS

1. Diketahui f(x) = 2√(x²+4) dan g(x) = √(x²+4) + 3x, maka (f-g) (x) adalah ….
A. √(x²+4) – 3x
B. -√(x²+4) + 3x
C. √(x²+4) + 3x
D. -√(x²+4) – 3x
E. 3√(x²+4) + 3x

 

Jawaban: A
Pembahasan:

Ingat bahwa (f-g)(x) = f(x) – g(x) sehingga kita peroleh
(f-g)(x) = f(x) – g(x)

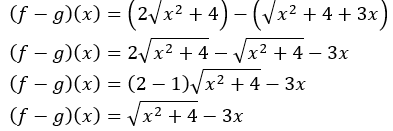
Topik: Fungsi Linear (NEW)
Subtopik: Fungsi Linear
Level Kognitif: LOTS

2. Grafik dari persamaan garis x+y=1 adalah ….

A.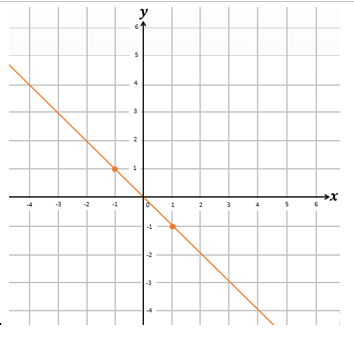

B.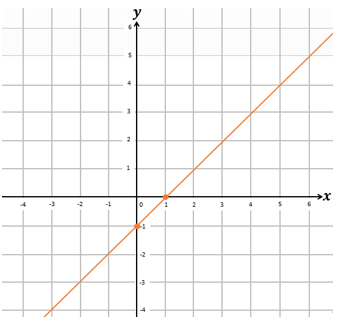

C.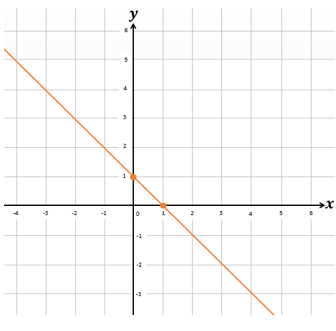

D.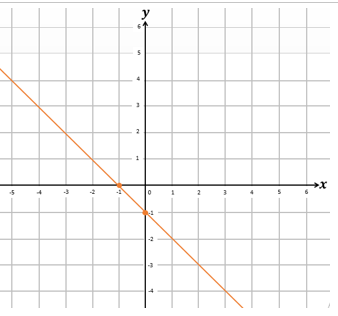

E.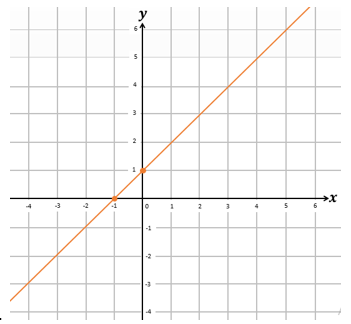

 

 

Jawaban: C
Pembahasan:

Akan kita gambarkan garis tersebut dengan dua titik. Kita cari titik potong garis tersebut terhadap sumbu X dan sumbu Y.

Jika x = 0 maka

(0)+y=1
y=1

Jika y=0 maka
x+(0)=1
x=1

Sehingga kita peroleh titik (0,1) dan (1,0). Dengan titik-titik tersebut, kita sambungkan satu garis lurus dua titik tersebut sehingga kita peroleh garis berikut.

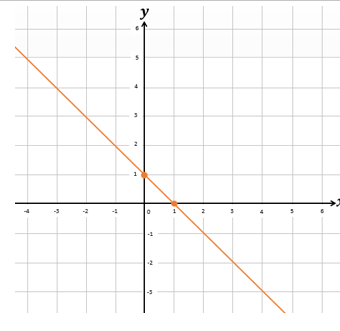
Topik: Fungsi Linear (NEW)
Subtopik: Persamaan Linear Satu Variabel
Level Kognitif: LOTS

3. Nilai x yang merupakan penyelesaian dari (x-1)/(x+2) = (x+1)/(x-3) adalah ….
A. 1/7
B. -1/7
C. 7
D. -7
E. 1

 

Jawaban: A
Pembahasan:
Perhatikan bahwa

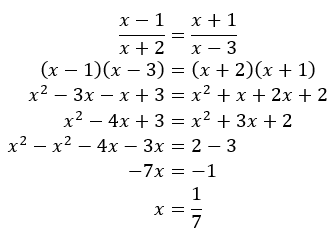
Selanjutnya, ingat bahwa penyebut tidak boleh 0. Artinya x+2≠0→x ≠ -2 dan x-3 ≠ 0→x ≠ 3.
Karena x=1/7 memenuhi syarat bahwa penyebut tidak 0 maka bisa kita simpulkan nilai x yang merupakan penyelesaian dari (x-1)/(x+2)=(x+1)/(x-3) adalah x=1/7.

Topik: Fungsi Irasional (NEW)
Subtopik: Pertidaksamaan Irasional
Level Kognitif: MOTS

4. Penyelesaian dari pertidaksamaan 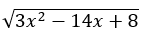>5 adalah ….

A. -1<x≤2/3 atau 4≤x<17/3
B. x<-1 atau x>17/3
C. x≤2/3 atau x≥4
D. -1<x<17/3
E. 2/3≤x≤4

Jawaban: B
Pembahasan:

Perhatikan bahwa

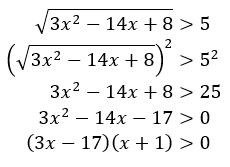
Perhatikan garis bilangan berikut

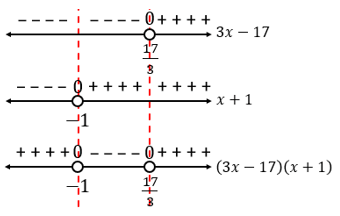
Karena tanda pertidaksamaannya adalah >, maka pilihlah daerah dengan tanda positif, yaitu x < -1 atau x > 17/3.

Selanjutnya perhatikan bahwa syarat fungsi di dalam bentuk akar harus lebih dari atau sama dengan 0, sehingga

3x² – 14x + 8 ≥ 0
(3x – 2)(x – 4) ≥ 0

Perhatikan garis bilangan berikut

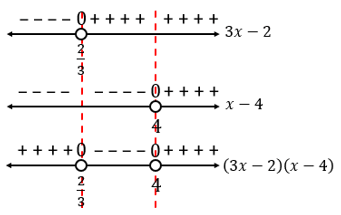
Karena tanda pertidaksamaannya adalah ≥, maka pilihlah daerah dengan tanda positif atau nol, yaitu x≤2/3 atau x≥4.

Irisan dari hasil yang telah didapatkan dan syaratnya yaitu

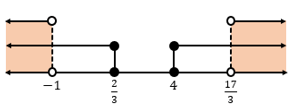
Sehingga penyelesaian dari pertidaksamaan 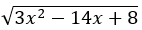> 5 adalah x<-1 atau x>17/3.

Topik: Fungsi Eksponen (NEW)
Subtopik: Sifat Bilangan Berpangkat II
Level Kognitif: LOTS

5. Jika 11^11-x = 3^x-11, maka nilai x yang memenuhi adalah ….

A. -11
B. -7
C. 0
D. 7
E. 11

Jawaban: E
Pembahasan:

Perhatikan bahwa

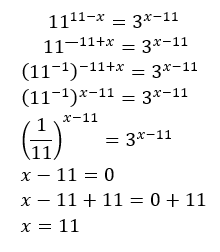
Topik: Fungsi Logaritma (NEW)
Subtopik: Aplikasi Bentuk Logaritma
Level Kognitif: MOTS

6. Jika ³log⁡2 = p dan ³log⁡7 = q maka ¹⁴log⁡36 =⋯

 

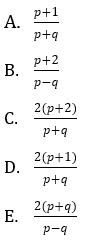
Jawaban: D
Pembahasan:

Perhatikan bahwa

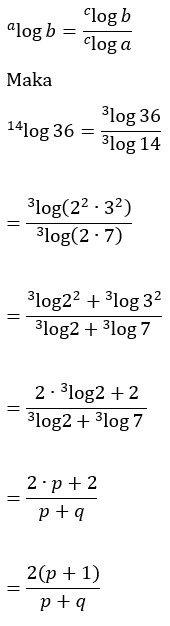
Topik: Sistem Persamaan dan Pertidaksamaan Linear-Kuadrat Dua
Subtopik: Sistem Persamaan Linear Kuadrat Dua Variabel (SPLKDV)
Level Kognitif: HOTS

7. Diketahui garis k melewati titik (5,4) dan menyinggung parabola y = x² – 5x + 4. Persamaan garis k adalah ….

A. y = 5x
B. y = -5x
C. y = 5x + 21
D. y = 5x – 21
E. y = -5x – 21

 

Jawaban: D
Pembahasan:

Misalkan persamaan garis k adalah y = mx + c dengan m adalah gradien garis tersebut.
Diketahui garis k melewati titik (5,4), maka kita punya

y = mx + c
4 = m(5) + c
4 = 5m + c
4 – 5m = c

Selanjutnya, kita subtitusikan c=4-5m ke y=mx+c sehingga

y=mx+c
y=mx+4-5m
y=m(x-5)+4

Kemudian, subtitusikan y = m(x-5) + 4 ke y = x² – 5x + 4 maka kita peroleh

y = x² – 5x + 4
m(x-5)+4 = x² – 5x + 4
mx – 5m + 4 = x² – 5x + 4
0 = x² – 5x – mx + 5m + 4 – 4
0 = x² + (-5-m)x + 5m

Karena garis k melewati titik (5,4) dan menyinggung parabola y = x² – 5x + 4 maka nilai diskriminan pada persamaan 0 = x² + (-5-m)x + 5m adalah nol, sehingga kita peroleh

D = 0
(-5-m)² – 4(1)(5m) = 0
25 + 10m + m² – 20m = 0
m² – 10m + 25 = 0
(m-5)² = 0
m – 5 = 0
m = 5

Maka, persamaan garis k adalah

y = m(x-5) + 4
y = 5(x-5) + 4
y = 5x – 25 + 4
y = 5x – 21

Topik: Matriks (NEW)
Subtopik: Operasi Hitung Matriks II
Level Kognitif: MOTS

8. Diketahui 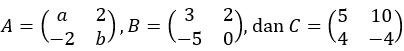. Nilai a dan b berturut-turut yang memenuhi AB=C adalah ….

A. -5 dan -2
B. -5 dan 2
C. -2 dan 5
D. 5 dan -2
E. 5 dan 2

 

Jawaban: D
Pembahasan:

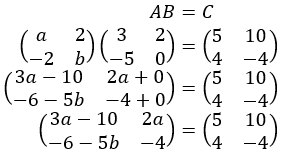
dari persamaan matriks di atas, kita peroleh

3a – 10 = 5
3a = 5 + 10
3a = 15
a = 15/3
a = 5

dan

-6 – 5b = 4
-5b = 4 + 6
-5b = 10
b = 10/(-5)
b = -2

Jadi, nilai a dan b berturut-turut adalah 5 dan -2.

Baca juga: Latihan Soal UNBK SMA Bahasa Indonesia Tahun 2020

Topik: Barisan dan Deret
Subtopik: Deret Geometri
Level Kognitif: HOTS

9. Diketahui sebuah deret geometri terdiri dari delapan suku. Jumlah tiga suku pertama 210 dan jumlah tiga suku terakhir 6720. Suku kelima deret tersebut adalah ….

A. 600
B. 480
C. 360
D. 240
E. 120

 

Jawaban: B
Pembahasan:

Diketahui:

n = 8
S₃ = 210
S₈ – S₅ = 6720

Maka,

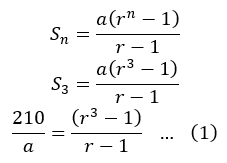
Kemudian

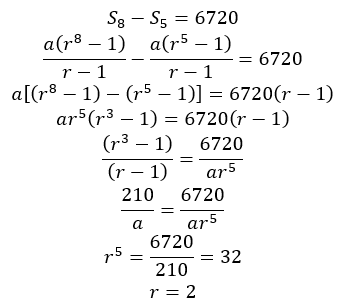
Sehingga,

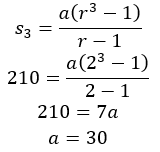
Maka diperleh suku kedua deret tersebut adalah:
U_n = ar^n-1

U₅ = 30∙2^5-1 = 30∙16 = 480

Topik: Limit II (NEW)
Subtopik: Limit Fungsi Trigonometri
Level Kognitif: LOTS

10. Nilai dari = ….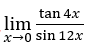

A. 4
B. 3
C. 1
D. 1/3
E. 1/4

 

Jawaban: D
Pembahasan:

Perhatikan bahwa

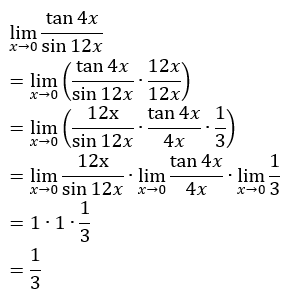
Topik: Turunan II (NEW)
Subtopik: Latihan Turunan Trigonometri
Level Kognitif: MOTS

11. Diketahui f(x) = sin⁡ (3x – π). Jika f’ (x) adalah turunan pertama dari f(x), maka f’ (π/3) adalah….

A. 3
B. 3/2
C. 0
D. -3/2
E. -3

 

Jawaban: A
Pembahasan:

f(x) = sin⁡(g(x))
f^’ (x) = cos ⁡(g(x)) . g'(x)

f(x) = sin⁡(3x-π)

f^’ (x) = cos⁡(3x-π) ∙ 3
f^’ (x) =3 cos⁡(3x-π)
f^’ (π/3) = 3 cos⁡(3(π/3)-π)
f^’ (π/3) = 3 cos⁡(0)
f^’ (π/3) = 3(1)

= 3

Topik: Integral II
Subtopik: Integral Fungsi Trigonometri
Level Kognitif: MOTS

12. Diketahui f(x) = (2 – 2 cos²⁡(x)) (1 + cot²⁡(x)) maka ∫f(x) dx= ….

A. 2x+C
B. x+C
C. 1/2 x+C
D. sin⁡x+C
E. cos⁡x+C

 

Jawaban: A
Pembahasan:

Ingat kembali bahwa

cot⁡(x) =cos⁡(x) / sin⁡(x)

Maka diperoleh,

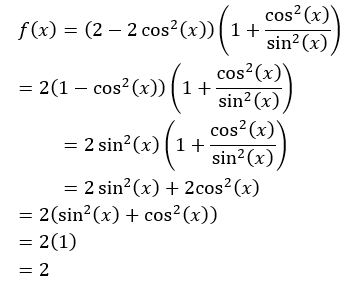
Sehingga integral fungsi tersebut adalah

∫f(x) dx = ∫2 dx

=2x+C

[separtor]

Topik: Bidang Ruang: Jarak (NEW!)
Subtopik: Jarak Titik ke Titik
Level Kognitif : LOTS

13. Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Jika titik P adalah titik tengah CG, maka jarak dari titik A ke titik P adalah …

A. 14 cm
B. 12√2 cm
C. 12 cm
D. 6√2 cm
E. 6 cm

 

Jawaban: C
Pembahasan:

 

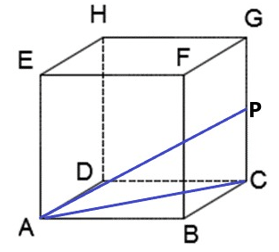
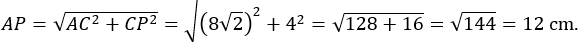
[serparaot]

Topik: Fungsi Kuadrat II (NEW)
Subtopik: Jarak Dua Titik Pada Grafik Fungsi Kuadrat
Level Kognitif: MOTS

14. Garis y = 2x + 13 dan kurva y = x² – 4x – 3 berpotongan di titik P(x₁,y₁ ) dan Q(x₂,y₂ ) , nilai dari (y₁+y₂ ) – (x₁ + x₂)= ….

A. 38
B. 32
C. 29
D. -32
E. -38

 

Jawaban: B
Pembahasan:

Pertama-tama substitusi persamaan garis ke persamaan kurva, sehingga didapat

x² – 4x – 3 = 2x + 13
x² – 4x – 3 – 2x – 13 = 0
x² – 6x – 16 = 0
(x – 8)(x + 2) = 0
x₁ = 8 atau x₂ = -2

Untuk mencari nilai y₁ dan y₂, subtitusi titik x₁ dan x₂ ke persamaan garis sehingga didapat

y₁ = 2x₁ + 13 = 2(8) + 13 = 29

Kemudian

y₂ = 2x₂ + 13 = 2(-2) + 13 = 9

Maka

(y₁ + y₂) – (x₁ + x₂ )
= (29+9) – (8+(-2))
= 38 – 6
= 32

Topik: Trigonometri
Subtopik: Perbandingan dan Sudut Istimewa
Level Kognitif: HOTS

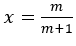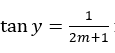15. Jika x dan y sudut-sudut di kuadran I, , dan maka nilai dari cos⁡4(x+y)=⋯

A. -1
B. 0
C. 1/2
D. 1
E. 3/2

 

Jawaban: A
Pembahasan :

Ingat rumus penjumlahan trigonometri berikut ini:

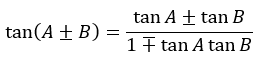
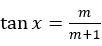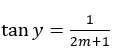Jika dan maka:

 

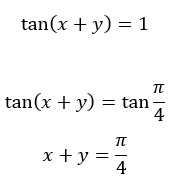
Sehingga,

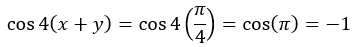
Topik: Statistika Deskriptif (NEW!)
Subtopik: Penyajian Data
Level Kognitif: MOTS

16. Perhatikan diagram lingkaran berikut yang menyatakan profesi yang ada di suatu kota A.

 

Jika total penduduk yang memiliki profesi di atas adalah 300 orang, banyak orang yang berprofesi sebagai petani adalah … orang.

A. 25
B. 50
C. 75
D. 125
E. 150

 

Jawaban: C
Pembahasan:

Diketahui bagian nelayan pada diagram lingkaran di atas adalah 25% dan total penduduk 300 orang. Maka, banyaknya penduduk yang berprofesi sebagai nelayan adalah

25% × 300 = 75 orang.

 

Topik: Aturan Pencacahan (NEW)
Subtopik: Kombinasi
Level Kognitif: MOTS

17. Terdapat sebuah kotak berisi 5 bola hitam dan 6 bolah putih. Joni mengambil 4 bola dari kotak tersebut. Banyak cara Joni mengambil maksimal 1 bola putih adalah ….

A. 60
B. 65
C. 90
D. 165
E. 215

 

Jawaban: B
Pembahasan:

Beberapa kasus yang terjadi dengan maksimal 1 bola putih adalah sebagai berikut:

3 bola hitam dan 1 bola putih, maka banyak caranya adalah

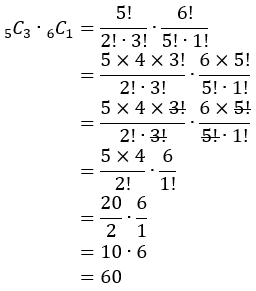
4 bola hitam, maka banyak caranya adalah

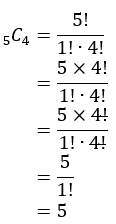
Jadi, total banyak caranya adalah 60 + 5 = 65.

Topik: Teori Peluang (NEW!)
Subtopik: Peluang I
Level Kognitif: LOTS

18. Diketahui tabel hasil percobaan pelemparan 20 buah dadu dengan 6 sisi sebagai berikut

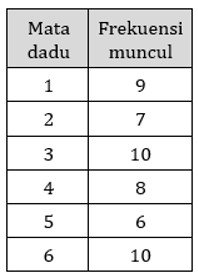
Frekuensi relatif muncul mata dadu 4 adalah ….

A. 4%
B. 10%
C. 16%
D. 20%
E. 40%

 

Jawaban: E
Pembahasan:

Perhatikan bahwa kejadian muncul mata dadu 5 memiliki frekuensi 6 kali. Karena banyaknya percobaan pelemparan dadu yang dilakukan adalah 20 kali, maka frekuensi relatif muncul mata dadu 5 adalah

8/20=40/100=40%

Topik: Aturan Pencacahan (NEW)
Subtopik: Permutasi
Level Kognitif: LOTS

19. Dalam sebuah kursi melingkar, terdapat 6 orang yang sedang duduk. Dua orang diantaranya memakai baju merah, dua orang lagi memakai baju kuning, dan sisanya memakai baju hijau. Orang yang memakai baju dengan warna yang sama duduknya disatukan, maka banyaknya cara mereka duduk adalah ….

A. 8
B. 9
C. 16
D. 64
E. 81

 

Jawaban: C
Pembahasan:

Diketahui:

Merah = 2 orang
Kuning = 2 orang
Hijau = 2 orang

Banyak cara = permutasi duduk melingkar × permutasi merah × permutasi kuning × permutasi hijau

Banyak cara = (3-1)! (2)! (2)! (2)! = 2!2!2!2! = 16

Topik: Aturan Pencacahan (NEW)
Subtopik: Kombinasi
Level Kognitif: MOTS

20. Dari 7 pria dan 4 wanita, akan dipilih 4 pria dan 2 wanita untuk duduk sebagai pengurus suatu organisasi. Bila 2 pria dan 1 wanita pasti dipilih maka banyaknya susunan pengurus yang mungkin dibentuk adalah ….

A. 12
B. 15
C. 30
D. 36
E. 45

 

Jawaban: C
Pembahasan:

Diketahui:

Pria = 7 orang, 2 sudah pasti terpilih maka sisa 5 orang pria.
Wanita = 4 orang, 1 sudah pasti terpilih maka sisa 3 orang wanita.

Kemudian ingat cara menghitung kombinasi r dari n objek adalah:

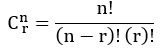
Cara memilih 2 pria dari 5 pria yang tersisa:

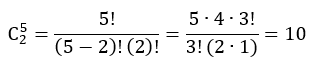
Cara memilih wanita yang tersisa:

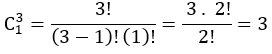
Total cara memilih pria dan wanita yang tersisa:
Banyak cara=banyak cara pria×banyak cara wanita = 10 × 3 = 30.

 

Nah, itulah berbagai soal matematika IPA yang bisa kamu pakai sebagai ajang latihan menyambut UNBK SMA 2020. Gimana? Udah sejauh mana materi yang kamu bisa? Kalau kamu ingin memahami materi-materi yang kamu anggap masih sulit, langsung aja tonton di ruangbelajar!