Rumus Luas dan Volume Bola, Cara Menghitung & Contohnya | Matematika Kelas 9

Yuk, kita belajar cara menghitung luas dan volume bola lewat artikel Matematika kelas 9 ini. Ada contoh soalnya juga, lho!

—

Guys, kalian tau nggak, ternyata menurut skala survei Indonesia, ada 90,8% masyarakat Indonesia yang mengetahui olahraga sepak bola. Nggak cuma itu aja, sebanyak 47,6% menyukainya. Persentase ini mengalahkan olahraga lainnya, seperti bulutangkis dengan persentase 18,8%.

Hmmm… nggak heran sih ya, terbukti dari banyaknya anak-anak kecil yang mengidolakan tokoh pemain bola, kayak Cristiano Ronaldo. Bahkan, orang dewasa pun sering begadang untuk nungguin klub kesayangannya tanding. Oh ya, nggak cuma laki-laki aja loh yang menyukai olahraga ini, banyak juga perempuan yang senang dengan sepak bola.

Tapi, kamu pernah kepikiran nggak sih, kalo bola sepak menggunakan bola dengan bentuk lain? Seperti misalnya bola rugby, kan bisa menggelinding juga tuh, coba deh bayangin!

Bola Rugby (Sumber Gambar: unsplash.com)

Hahaha, iya sih bisa menggelinding, tapi pasti bakalan susah banget. Udah gitu, pemain sepak bola akan susah ketika mengoper ke temannya.

Nah, dari sini kita bisa tau ya, bola sepak bisa menggelinding dengan baik, dan pemain pun bisa dengan mudah menggiring, mengoper, dan menendang bola ke gawang. Rahasianya adalah karena bola sepak termasuk  bangun ruang sisi lengkung.

Apa itu Bangun Ruang Bola?

Bola adalah bangun ruang sisi lengkung yang dibentuk dari setengah lingkaran yang diputar mengelilingi garis tengahnya.

Kerangka Bola (sumbe Youtube: Omega Open Course)

Sifat-Sifat Bangun Ruang Bola

Untuk bisa lebih mengenal bola, kita harus tau sifat-sifatnya. Kamu bisa ingat sifat-sifat bola ini ya:

1. Memiliki satu titik pusat.
2. Tidak memiliki titik sudut.
3. Tidak memiliki rusuk.
4. Tidak memiliki diagonal bidang dan diagonal ruang.
5. Memiliki satu sisi yang disebut dinding bola.
6. Memiliki jari-jari (r), yaitu jarak titik pusat ke dinding bola.
7. Terdapat diameter (d), yaitu jarak dinding ke dinding melewati titik pusat.

Jenis-Jenis Bangun Ruang Bola

Btw, kamu tau nggak kalo bola itu terbagi jadi 2 macam? yaitu bola pejal dan bola berongga. Apa sih bedanya?

Bola pejal adalah bola padat, yang volumenya selalu berisi. Contoh gampangnya tuh kayak bakso. Semantara itu, bola berongga adalah bola biasa yang dalamnya tidak berisi. Contohnya tuh, bisa tahu bulat wkwkwk, atau bola plastik mainan bayi, dan masih banyak lagi.

Setelah kamu tau sifat, dan macam-macam bola, sekarang cari tahu rumus dari luas dan volume bola, yuk!

Rumus Volume Bola dan Contoh Soal

Sebenarnya sama aja sih kayak bangun ruang lainnya, bola punya luas dan volumenya sendiri. Tapi, sebelum ke volume bola, kamu udah harus paham volume kerucut ya, karena keduanya berhubungan.

Baca Juga: Cara Menghitung Luas dan Volume Kerucut

Ilustrasinya gini, misal kita isi kerucut penuh dengan air, setelah itu air dari kerucut kita pindahkan ke bola. Ternyata, dibutuhkan 2 kerucut penuh air untuk mengisi semua ruang bola. Supaya kamu lebih kebayang, kamu bisa perhatikan video di bawah ini dulu ya!

(Sumber Youtube: Kyle Pearce)

Lewat video di atas, kita bisa nemuin rumus volume bola. Tapi, ada yang harus di-highlight nih guys, tinggi kerucut itu 2 kali jari-jari bola, ya. Jadi, dengan jari-jari yang sama antar kedua bangun (kerucut dan bola), maka volume bola adalah 2 × volume kerucut.

Bisa ditulis, jadi kaya gini ya guys:

Nah, supaya makin paham, langsung masuk ke contoh soal ya.

Terdapat benda pejal berbentuk seperempat bola dengan diameter 20 cm. Volume benda tersebut adalah …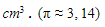

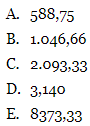
Pembahasan:

Diameter bola = 20 cm, r = 10 cm.

Bentuk seperempat bola pejal, maka rumusnya seperti ini,

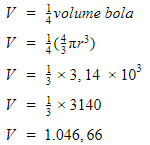
Maka jawaban yang tepat adalah B. 1046,66.

Gimana, gampang, kan?

Next, kita bahas rumus luas permukaan bola, yuk!

Rumus Luas Permukaan Bola dan Contoh Soal

Kalo tadi volume bola sama dengan 2 × volume kerucut, nah kalo luas permukaan bola bisa dihitung lewat luas persegi panjang. Persegi panjang itu kan punya 2 sisi, yaitu panjang dan lebar.

Nah, sisi panjangnya sama dengan keliling lingkaran, terus untuk lebarnya sama dengan 2 jari-jarinya.

Ilustrasi Luas Permukaan Bola (Sumber Youtube: 3Blue1Brown)

Sesuai ilustrasi di atas, bisa disusun rumusnya ya. Ini dia rumus luas permukaan bola. Kamu wajib ingat!

Oke, sekarang kalo seandainya ada bola terus kita potong dengan bagian yang sama, menurut kamu luas permukaannya masih sama nggak? Enggak ya guys. Rumus luas setengah permukaan bola tinggal kita kalikan setengah aja. Jadi gini ya guys!

Tapi, khusus untuk rumus luas permukaan setengah bola pejal beda lagi ya. Loh kok gitu? itu karena bola pejal berisi. Kamu bayangin aja ketika kamu memotong semangka jadi 2 bagian yang sama besar. Kamu bakal nemuin permukaan yang berbentuk lingkaran. Jadi luas permukaan setengah bola tadi ditambah luas lingkaran. Penulisannya, kayak gini:

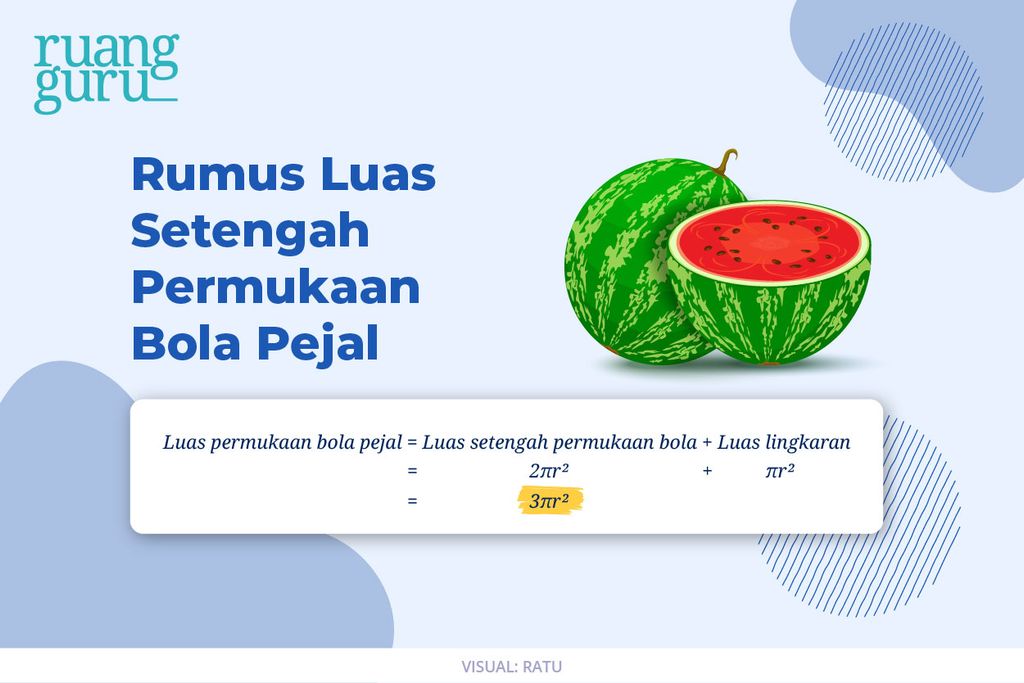
Rumus-rumus itu bisa kita aplikasikan di contoh soal ini ya, guys!

Jika luas permukaan bola adalah 1.808,64 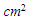berapakah diameter bola tersebut?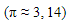

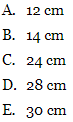
Pembahasan:

Diketahui luas permukaan bola adalah 1.808,64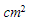

Karena yang ditanya adalah diameter, dimana diameter adalah 2 × jari-jari, sehingga 2 × 12= 24 cm.

Baca Juga: Rumus Volume Tabung, Luas Permukaan & Keliling Alas

Lewat beberapa rumus yang udah kita pelajarin, jangan kebalik dan bingung ya guys. Oh ya, ada sedikit tips nih, waktu kamu lagi baca soal tentang bola, sebisa mungkin sambil kamu bayangkan ya. Karena, dari situlah kamu bisa menggunakan rumus yang tepat dan nggak kebingungan walaupun soal yang dikasih bervariasi.

Bonus tips buat kamu! Inget ya jangan berhenti sampai disini aja. Kamu harus banget latihan soal-soal di ruangbelajar. Semua soalnya diupdate terus menerus, dan kamu bisa langsung dapat pembahasannya, ditambah ada pembahasan konsep langsung dari master teacher ruangguru yang asik banget. Yuk, tunggu apalagi, langganan sekarang ya, dadah!

Referensi:

Subchan, Winarni, Hanafi L, dkk. (2015) Matematika SMP/MTs Kelas IX Semester 1. Jakarta: Kementerian Pendidikan dan Kebudayaan

Sumber Gambar dan Video:

“But why is a sphere’s surface area four times its shadow?”. [Daring] Tautan: https://www.youtube.com/watch?v=GNcFjFmqEc8&t=616s (diakses pada tanggal 26 Oktober 2021)

Spherical Coordinate System. [Daring] Tautan: https://www.youtube.com/watch?v=FDyenWWlPdU&t=160s (diakses pada tanggal 25 Oktober 2021)

Visualizing the volume of a Sphere Formula. [Daring]. Tautan: https://www.youtube.com/watch?v=YNutS8eIhEs  (diakses pada tanggal 25 Oktober 2021)