Peluang: Percobaan, Titik Sampel & Ruang Sampel | Matematika Kelas 8

Belajar tentang peluang matematika, yuk! Mulai dari melakukan percobaan, hingga cara menyusun titik sampel dan ruang sampel dari percobaan. Siapkan dadu dan uang koin, ya!

—

Kamu pernah main ular tangga? Saat bermain ular tangga, sebelum menggerakkan pion, kita harus melempar dadu terlebih dahulu. Nah, ketika kita melempar dadu, kira-kira ada berapa kemungkinan mata dadu yang akan muncul?

Yup, betul! Ada 6 kemungkinan. Kenapa bisa 6? Karena jumlah mata dadu itu ada 6, yaitu angka 1, 2, 3, 4, 5, dan 6. Eits, tapi hal ini hanya berlaku jika dadu yang dilempar hanya satu buah, ya. Kalau dadu yang dilempar ada dua buah, maka jumlah kemungkinannya akan lebih banyak lagi karena jumlah mata dadunya pun lebih banyak.

Throw the dice! (Sumber: giphy.com)

Pelemparan dadu seperti ini adalah contoh dari percobaan yang akan kamu pelajari pada materi peluang kali ini. Apa yang dimaksud dengan percobaan?

Percobaan

Percobaan adalah suatu tindakan atau kegiatan untuk memperoleh hasil tertentu. Percobaan disebut juga dengan eksperimen. Contoh percobaan antara lain melempar dadu, melempar uang koin, mengambil kartu secara acak dari tumpukan kartu, dan lain-lain.

Baca Juga: Mengenal Statistika dan Diagram Penyajian Data

Dengan melakukan percobaan, kita bisa mendapatkan hasil atau disebut juga sebagai titik sampel. Apa yang dimaksud dengan titik sampel?

Titik Sampel

Titik sampel adalah hasil dari percobaan. Misalnya, kita melakukan percobaan melempar satu buah dadu, maka titik sampelnya adalah (1), (2), (3), (4), (5), dan (6). Sementara itu, jika kita melakukan percobaan melempar satu buah uang koin, maka titik sampelnya adalah (A) dan (G). A berarti Angka dan G berarti Gambar.

Contoh lainnya, misalnya kita melemparkan dua buah uang koin, maka titik sampelnya adalah (A, A), (A, G), (G, A), dan (G, G).

Sudah paham ya, sampai sini? Sekarang, lanjut ke pembahasan ruang sampel, yuk!

—

Eits, tapi sebelum itu, kalau kamu ada pertanyaan terkait materi atau tugas di sekolah, kamu bisa tanyakan ke Roboguru, ya! Pertanyaan sesulit apapun akan bisa dijawab dengan mudah oleh Roboguru!

Ruang Sampel

Ruang sampel adalah himpunan dari titik sampel. Ruang sampel juga biasa disebut dengan semesta dan disimbolkan dengan S. Ruang sampel berisi seluruh titik sampel yang ada, alias semua kemungkinan yang dapat muncul pada suatu percobaan.

Kita ambil contoh dari percobaan pada pembahasan titik sampel tadi. Percobaan pertama yaitu melempar satu buah dadu, dengan titik sampelnya adalah (1), (2), (3), (4), (5), dan (6). Maka, ruang sampelnya adalah S = {1, 2, 3, 4, 5, 6}.

Kemudian, percobaan kedua yaitu melempar satu buah uang koin, dengan titik sampelnya adalah (A) dan (G). Maka, ruang sampelnya adalah S = {A, G}.

Terakhir, percobaan ketiga yaitu melemparkan dua buah uang koin, dengan titik sampelnya adalah (A, A), (A, G), (G, A), dan (G, G). Maka, ruang sampelnya adalah S = {(A, A), (A, G), (G, A), (G, G)}.

Baca Juga: Pengertian, Sifat, dan Rumus Kubus Disertai Contoh

Gampang, kan? Sekarang, kita lanjut ke cara menyusun anggota ruang sampel, ya.

Cara Menyusun Anggota Ruang Sampel

Ada tiga cara untuk menyusun anggota ruang sampel, yaitu dengan cara mendaftar, menggunakan diagram pohon, dan menggunakan tabel. Kita bahas satu per satu, yuk!

Cara Menyusun Anggota Ruang Sampel dengan Mendaftar

Cara pertama adalah menyusun anggota ruang sampel dengan mendaftar alias menuliskan seluruh anggota ruang sampel secara berurutan. Cara ini bisa dipilih ketika anggota ruang sampelnya tidak terlalu banyak.

Contohnya, saat kita melemparkan dua buah koin sekaligus, maka titik sampel atau semua hasil yang mungkin terjadi dari percobaan tersebut adalah (A, A), (A, G), (G, A), dan (G, G).

Maka, diperoleh ruang sampel:

S = {(A, A), (A, G), (G, A), (G, G)}

Banyak anggota ruang sampel → n(S) = 4

Cara Menyusun Anggota Ruang Sampel dengan Diagram Pohon

Cara kedua adalah menyusun anggota ruang sampel dengan diagram pohon. Cara ini bisa dipilih ketika anggota ruang sampelnya cukup banyak dan akan memakan waktu jika menggunakan cara mendaftar.

Contohnya, saat kita melemparkan satu buah uang koin dan satu buah dadu, maka kemungkinan kejadiannya adalah munculnya angka (A) atau gambar (G) pada koin, dan salah satu mata dadu pada dadu.

Misalkan, uang koin dianggap bagian pertama, sementara dadu dianggap bagian kedua, maka bisa digambarkan diagram pohon sebagai berikut:

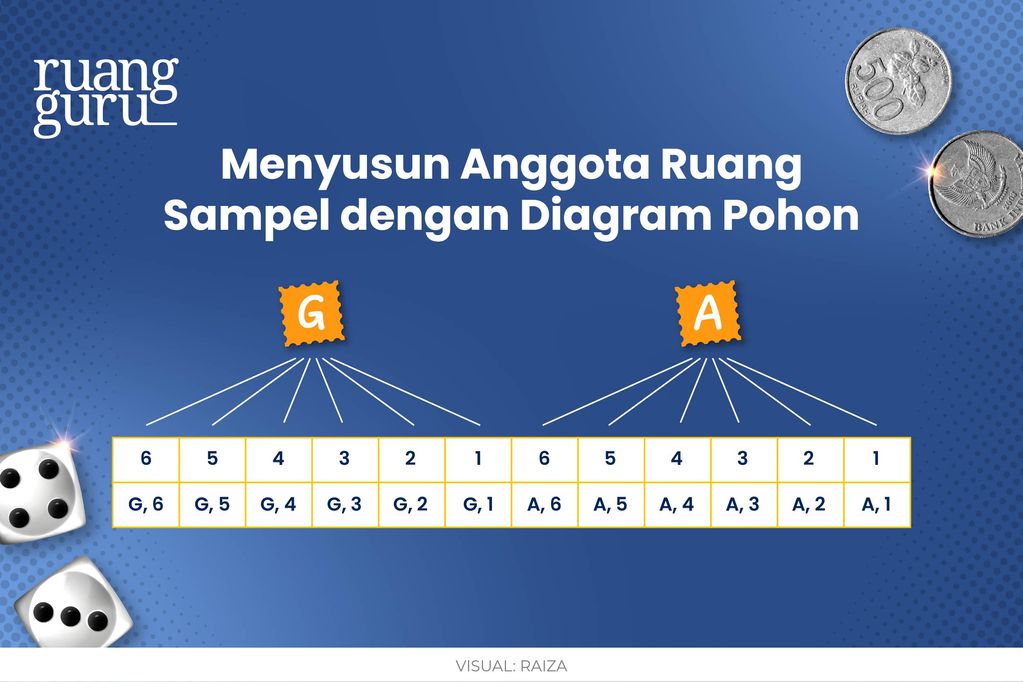
Maka, diperoleh ruang sampel:

S = {(A, 1), (A, 2), (A, 3), (A, 4), (A, 5), (A, 6), (G, 1), (G, 2), (G, 3), (G, 4), (G, 5), (G, 6)}

Banyak anggota ruang sampel → n(S) = 12

Baca Juga: Unsur-Unsur Lingkaran Ada Apa Saja, Ya?

Cara Menyusun Anggota Ruang Sampel dengan Tabel

Cara ketiga adalah menyusun anggota ruang sampel dengan tabel. Cara ini bisa dipilih ketika anggota ruang sampelnya sangat banyak dan akan memakan waktu jika menggunakan cara mendaftar maupun diagram pohon.

Contohnya, saat kita melemparkan dua buah dadu sekaligus, maka pada masing-masing dadu akan ada 6 kemungkinan kejadian yang muncul, yaitu mata dadu 1, 2, 3, 4, 5, dan 6. Jika kita susun dalam sebuah tabel, maka didapatkan hasil sebagai berikut:

Maka, diperoleh ruang sampel:

S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

Banyak anggota ruang sampel → n(S) = 36

—

Itu dia penjelasan tentang materi peluang matematika tentang percobaan, titik sampel, ruang sampel, serta cara menyusun anggota ruang sampel. Apakah kamu sudah paham? Mau belajar materi Matematika kelas 8 dengan lebih asyik dengan ribuan video belajar beranimasi menarik? Daftar ruangbelajar, yuk!

Referensi:

Subchan, Winarni, Hanafi L, dkk. (2015). Matematika SMP/MTs Kelas IX. Jakarta: Kementerian Pendidikan dan Kebudayaan.

Sumber Gambar:

GIF ‘Dadu’ [Daring]. Tautan: https://giphy.com/gifs/heyarnold-hey-arnold-nicksplat-3ohjUS2N88LGAjLypO (Diakses: 7 April 2022)

Artikel ini diperbarui pada 29 Mei 2024.