Cara Menyelesaikan Sistem Persamaan Linear Dua Variabel (SPLDV) | Matematika Kelas 8

Pada artikel Matematika kelas 8 kali ini, kamu akan mempelajari tentang cara menyelesaikan Sistem Persamaan Linear Dua Variabel (SPLDV) dan contoh soalnya. Ada metode grafik, metode substitudi, metode eliminasi, dan metode campuran.

—

Tu, wa, yah malah nyangkut! (sumber: giphy.com)

Lihat! Ada yang sedang berolahraga! Kumamon si maskot beruang lucu asal Jepang ini sepertinya ingin melakukan lompat tali, ya. Tapi, sayangnya, tali yang digunakan terlalu pendek, nih. Jadi, nyangkut deh di tubuh gembulnya Kumamon.

Kamu tahu nggak, nih. Ternyata, masalah Kumamon ini bisa diselesaikan dengan menggunakan Matematika, lho, yaitu dengan penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV). Nah, untuk menyelesaikan masalah dengan menggunakan SPLDV ini, kita harus melewati langkah-langkahnya dulu. Jadi, nggak bisa asal-asalan dalam menentukan solusinya.

Mau tahu apa saja langkah-langkahnya? Yuk, simak penjelasannya pada artikel berikut ini!

Mengenal Sistem Persamaan Linear Dua Variabel (SPLDV)

Oh iya, sebelum itu, kita ketahui dulu yuk, apa itu SPLDV. Di kelas 7, tentunya, kamu sudah mempelajari materi tentang Persamaan Linear Satu Variabel (PLSV), ya. Selain ada PLSV, ada juga yang namanya Persamaan Linear Dua Variabel (PLDV), nih.

Lalu, apa sih bedanya PLSV dengan PLDV? Bedanya, kalau PLSV, persamaannya hanya memiliki satu variabel saja, sedangkan PLDV, persamaannya memiliki dua variabel. Nah, variabel-variabel ini hanya memiliki pangkat atau derajat bernilai satu. Kamu bingung nggak, nih? Kalau bingung, yuk, coba perhatikan perbedaan contoh PLSV dan PLDV di bawah ini! 

Baca Juga: Bagaimana Cara Menentukan Persamaan Garis Lurus?

Bentuk Umum Sistem Persamaan Linear Dua Variabel (SPLDV)

Bagaimana, sudah paham kan letak perbedaannya? Apabila terdapat dua atau lebih PLDV yang memiliki hubungan satu sama lain dan memiliki satu buah penyelesaian, maka itulah yang dinamakan dengan SPLDV. Bentuk umum SPLDV adalah sebagai berikut:

SPLDV ini biasanya digunakan untuk menyelesaikan masalah sehari-hari yang membutuhkan penggunaan Matematika, seperti menentukan harga suatu barang, mencari keuntungan penjualan, sampai menentukan ukuran suatu benda seperti masalah Kumamon di atas, lho.

Langkah-Langkah untuk Menyelesaikan Masalah dengan SPLDV

Oh iya, seperti yang sudah dituliskan sebelumnya, terdapat langkah-langkah tertentu untuk menyelesaikan masalah dengan menggunakan SPLDV, yaitu:

1. Mengganti setiap besaran yang ada di masalah tersebut dengan variabel (biasanya dilambangkan dengan huruf atau simbol).
2. Membuat model Matematika dari masalah tersebut. Model Matematika ini dirumuskan mengikuti bentuk umum SPLDV.
3. Mencari solusi dari model permasalahan tersebut dengan menggunakan metode penyelesaian SPLDV.

Nah, karena kamu sudah tahu apa saja langkah-langkahnya, sekarang, ayo kita bantu selesaikan masalah Kumamon!

Penyelesaian:

Langkah pertama yang harus kita lakukan adalah mengganti semua besaran yang ada di dalam soal dengan variabel. Kita misalkan:

x = panjang tali (dalam cm) dan y = tinggi badan (dalam cm)

Lalu, kita buat model Matematika dari permasalahan tersebut.

Panjang tali 70 cm lebih pendek dari tinggi Kumamon → x = y – 70 atau -x + y = 70

Dua kali panjang tali 30 cm lebih panjang dari tinggi Kumamon → 2x = 30 + y atau 2x – y = 30

Sehingga, diperoleh model Matematika-nya sebagai berikut:

Persamaan I: -x + y = 70

Persamaan II: 2x – y = 30

Sampai di sini kamu paham, kan? Nah, langkah selanjutnya, kita akan mencari nilai x dan y sebagai solusi dari masalah di atas dengan menggunakan metode penyelesaian SPLDV. Ternyata, metode penyelesaian SPLDV ini nggak hanya satu saja, melainkan ada empat macam metode penyelesaian yang akan dibahas di bawah ini. So, simak terus, ya!

Baca Juga: Perbedaan Persamaan dan Pertidaksamaan Linear

Metode Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV)

Terdapat 4 metode yang dapat digunakan untuk menyelesaikan SPLDV, di antaranya metode grafik, metode eliminasi, metode substitusi, dan metode campuran. Yuk, simak masing-masing penjelasannya disertai contoh soal!

1. Metode Grafik

Pada metode grafik, kita akan menggambar grafik dari dua buah persamaan yang telah kita buat pada langkah sebelumnya. Cara yang paling mudah untuk menggambar grafik adalah dengan mencari titik potong terhadap sumbu x dan sumbu y. Berdasarkan contoh di atas, kita dapat menentukan titik potong dari masing-masing persamaan sebagai berikut:

Contoh soal dan penyelesaian SPLDV menggunakan metode grafik:

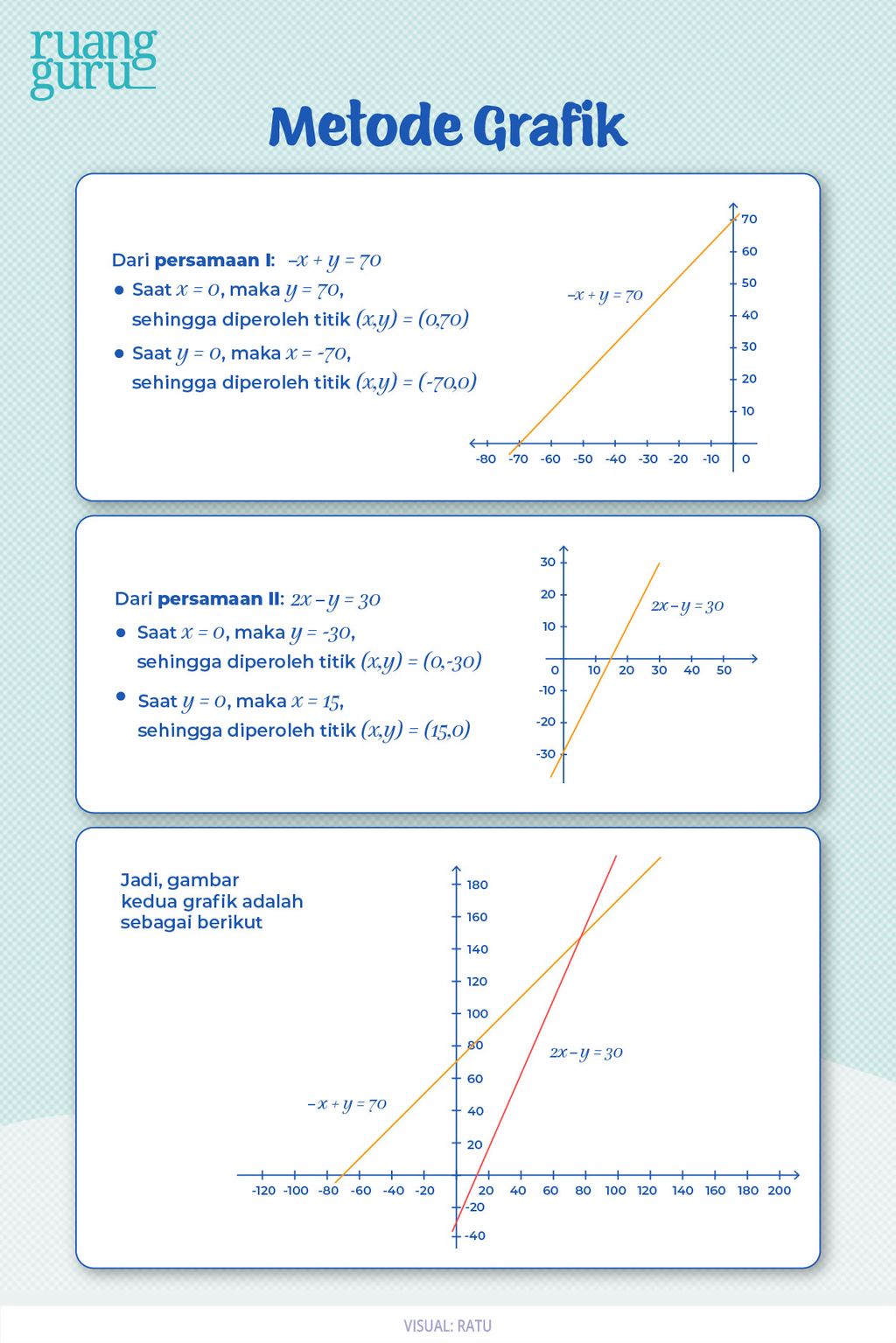
Sehingga, diperoleh titik potong dari kedua garis yaitu (x,y) = (100,170). Sebelumnya, kita telah memisalkan panjang tali dengan variabel x dan tinggi Kumamon dengan variabel y. Jadi, sudah dapat ditentukan nih berapa panjang tali dan juga tinggi si Kumamon itu. Yap! Jawabannya adalah 100 cm untuk panjang tali dan 170 cm untuk tinggi Kumamon.

Bagaimana, mudah, kan? Metode grafik ini biasanya berguna jika nilai koefisien dan nilai konstanta dari persamaannya bukan merupakan bilangan bulat, sehingga lebih baik digambar untuk memudahkan mencari nilai x dan y nya.

2. Metode Eliminasi

Metode yang kedua adalah metode eliminasi. Metode ini bertujuan untuk mengeliminasi (menghilangkan) salah satu variabel, sehingga nilai variabel lainnya bisa diketahui. Caranya dapat kamu lihat pada contoh di bawah ini.

Contoh soal dan penyelesaian SPLDV menggunakan metode eliminasi:

Berdasarkan metode eliminasi, diperoleh nilai x = 100 dan y = 170. Jadi, dapat diketahui kalau panjang tali adalah 100 cm dan tinggi badan Kumamon adalah 170 cm. Sampai sini, menurut kamu, lebih mudah pakai metode yang mana, nih? Hehe…

Baca Juga: Sistem Koordinat Kartesius dan Cara Membuat Grafiknya

3. Metode Substitusi

Metode substitusi bertujuan untuk mengganti nilai suatu variabel pada suatu persamaan dari persamaan lainnya. Hah?! Gimana, gimana? Tenang, kalau bingung, caranya dapat kamu lihat ada contoh berikut ini:

Contoh soal dan penyelesaian SPLDV menggunakan metode substitusi:

Berdasarkan metode substitusi, diperoleh nilai x = 100 dan y = 170. Jadi, dapat diketahui kalau tinggi badan Kumamon adalah sebesar 170 cm dan tali yang dipakai Kumamon untuk bermain lompat tali adalah 100 cm.

4. Metode Campuran (Gabungan)

Metode ini merupakan gabungan dari metode eliminasi dan substitusi. Caranya, kamu dapat menggunakan metode eliminasi untuk mencari nilai x terlebih dahulu, kemudian ganti variabel x dengan nilai x yang sudah diperoleh dengan menggunakan metode substitusi untuk memperoleh nilai y. Atau sebaliknya, ya. Paham, nggak? Yuk, kita simak baik-baik caranya pada contoh di bawah ini!

Contoh soal dan penyelesaian SPLDV menggunakan metode gabungan:

Berdasarkan metode gabungan, diperoleh nilai x = 100 dan y = 170. Sehingga, dapat diketahui kalau panjang tali adalah sebesar 100 cm dan tinggi Kumamon adalah 170 cm. Perlu kamu ketahui kalau metode gabungan ini merupakan metode yang paling banyak dipakai untuk menyelesaikan masalah SPLDV.

Nah, kalau kamu perhatikan, dari keempat metode penyelesaian SPLDV di atas, akan diperoleh hasil yang sama. Jadi, bebas sebenarnya mau pakai metode yang mana saja. Meskipun begitu, kamu harus tetap menguasai keempat-empatnya, ya.

Selanjutnya, kita akan mencari tahu berapa panjang tali yang diperlukan agar Kumamon dapat bermain lompat tali tanpa harus tersangkut di tubuh gemoynya. Jika kamu membaca kembali contoh soal di atas, maka dapat diketahui kalau setidaknya, tali tersebut harus dua kali lebih panjang dari ukuran sebelumnya (2x). Jadi, sudah dapat kita ketahui ya, kalau panjang tali yang diperlukan agar tidak tersangkut di tubuh gemoy Kumamon adalah 2x = 2(100) = 200 cm.

Baca Juga: Cara Mencari Kemiringan (Gradien) pada Garis Lurus

Oke, apa tanggapanmu setelah mempelajari keempat metode penyelesaian SPLDV di atas? Easy bukan? Meskipun kelihatannya panjang dan rumit, tapi jika kamu memperbanyak latihan soal, pasti akan mudah, kok.

Oh iya, bagi kamu yang masih bingung dengan materi ini, jangan ragu untuk tuliskan pertanyaanmu di kolom komentar, ya. Kamu juga bisa lho mempelajari materi ini dalam bentuk video menarik bareng Master Teacher yang asik lewat ruangbelajar. Belajar jadi mudah dan pastinya banyak latihan soal yang bikin kamu antiremed!

Referensi:

As’ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017) Matematika SMP/MTs Kelas VIII Semester 1. Jakarta: Kementerian Pendidikan dan Kebudayaan

Sumber foto:

GIF ‘Kumamon Loncat’ [Daring]. Tautan: https://giphy.com/gifs/kumamon-LVWzUCdGioDBe (Diakses: 23 Desember 2020)