Garis Istimewa dan Dalil yang Berkaitan Pada Segitiga | Matematika Kelas 12

Artikel ini membahas mengenai macam-macam garis istimewa pada segitiga serta dalil-dalil yang berkaitan dengan segitiga.

—

Squad, coba sebutkan macam-macam bangun datar?

Persegi, persegi panjang, lingkaran, segitiga, jajargenjang, trapesium, apa lagi hayoo…

Wah, mantap nih masih ingat semua! Wajar saja ya karena topik bangun datar sudah kamu pelajari sejak duduk di bangku SD, mulai dari mengenal macam-macam bangun datar hingga mempelajari cara menghitung luas dan kelilingnya. Aplikasi dari bentuk bangun datar juga banyak ditemukan disekitar kita. Contohnya saja persegi panjang. Sadar nggak sih kalau setiap hari kamu selalu menggunakan benda yang bentuknya mirip persegi panjang? Yap, betul, handphone kamu, tuh. Hehe…

Setiap bangun datar memiliki ciri dan sifat yang berbeda-beda. Hal ini yang membuat masing-masing dari mereka unik, Squad. Tapi, tahukah kamu, ada satu bangun datar yang punya keistimewaan lebih dari bangun datar yang lain. Pasti kamu sudah tahu, ya? Ia adalah segitiga. Alasannya, segitiga memiliki empat macam garis yang disebut garis istimewa. Wah, apa ya yang menyebabkan dia istimewa? Selain itu, ada juga dalil-dalil yang berkaitan dengan segitiga, lho. Hmm… apa saja ya kira-kira? Yuk, kita cari tahu jawabannya lewat artikel ini!

Garis Istimewa pada Segitiga

Pasti kamu sudah tahu dong seperti apa bentuk segitiga. Yap, terdiri dari tiga garis lurus yang saling berhubungan dan membentuk tiga sudut yang berjumlah 180^o. Jika kita buat satu garis lurus di dalam segitiga yang menghubungkan satu sudut atau satu titik pada sisi segitiga dengan sisi di hadapannya mengikuti aturan tertentu, maka garis itulah yang dinamakan garis istimewa pada segitiga. Nah, seperti yang sudah kamu ketahui, terdapat empat macam garis istimewa pada segitiga, diantaranya sebagai berikut:

Lalu, apa sih yang menyebabkan keempat garis itu istimewa? Oke, setelah kamu perhatikan baik-baik gambar di atas, keempat garis tersebut ternyata tidak dibuat secara sembarangan, melainkan ada aturannya masing-masing. Akibatnya, munculah suatu sifat yang berkaitan dengan perbandingan antara sisi-sisi segitiga tersebut.

Contohnya saja pada garis bagi. Dijelaskan bahwa garis bagi merupakan suatu garis yang ditarik dari satu titik sudut ke sisi di hadapannya dengan aturan sudut tersebut harus terbagi menjadi dua sama besar. Sehingga, berlaku perbandingan antara sisi depan sudut dengan sisi-sisi pembentuk sudut segitiga tersebut (AD/DB = CA/BC). Tapi, kenapa sih bisa begitu? Nah, untuk pembuktiannya bisa kamu lihat pada gambar di bawah ini:

Sekarang, kamu sudah tahu kan kenapa empat garis di atas bisa dikatakan istimewa. Selanjutnya, seperti biasa nih, kurang lengkap kalau kita belajar matematika tanpa latihan soal. Jadi, boleh lah ya kita kerjakan satu soal di bawah ini. Tenang saja, kita kerjakan sama-sama, kok.

Contoh soal:

Hitunglah panjang BQ pada segitiga berikut:

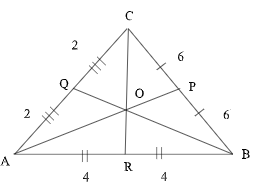
Penyelesaian:

Garis BQ adalah garis berat dari segitiga ABC, sehingga berlaku BQ² = ½BC² + ½AB² – ¼CA².

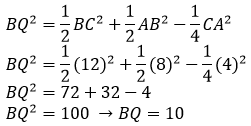
Gimana, mudah, kan? Kalau gitu, kita lanjut ke materi berikutnya ya, yaitu dalil-dalil yang berkaitan dengan segitiga.

Dalil-dalil pada Segitiga

Mungkin sebagian diantara kamu ada yang merasa bingung,

“Dalil itu apa, sih?”

Squad, perlu kamu ketahui nih, dalil (teorema) sering sekali digunakan dalam matematika, lho. Dalil (teorema) merupakan kebenaran yang diturunkan dari suatu aksioma. Kebenaran ini perlu dibuktikan, jadi tidak hanya berupa pernyataan saja. Nah, aksioma sendiri adalah suatu pernyataan yang dijadikan pedoman dasar, sehingga tidak memerlukan pembuktian. Saat ini, mungkin kamu jarang menemukan istilah-istilah tersebut. Tapi, bagi kamu yang tertarik untuk masuk jurusan Matematika, membuktikan suatu dalil atau teorema adalah hal yang biasa, lho. Wah, keren banget, kan?

Oke, back to the topic, ya. Ada empat macam dalil yang berkaitan dengan segitiga, yaitu:

1. Dalil Titik Tengah Segitiga

Dalil titik tengah segitiga berbunyi:

“Ruas garis yang menghubungkan titik-titik tengah pada dua sisi segitiga akan sejajar dengan sisi ketiga segitiga. Panjang ruas garis tersebut adalah setengah dari panjang sisi ketiga segitiga”.

Hmm… Kamu paham nggak nih sama maksud dalilnya? Oke, jadi gini Squad, jika kamu perhatikan gambar di bawah, titik E adalah titik tengah sisi AB dan titik D adalah titik tengah sisi AC. Sehingga, terbentuklah ruas garis ED. Nah, garis ED ini akan sejajar dengan garis BC dan kita dapat menghitung panjang ED, yaitu ED = ½ BC. Gimana? Paham ya sekarang?

2. Dalil Proyeksi

Rumus dalil proyeksi pada segitiga dapat dicari dengan memproyeksikan salah satu sisi segitiga dengan sisi segitiga yang lain. Tapi, masih ingatkah kamu apa itu proyeksi? Nah, proyeksi adalah pemetaan suatu daerah, bisa titik, garis, atau bidang secara tegak lurus terhadap daerah lainnya. Dalil proyeksi pada segitiga terbagi menjadi dua, yaitu dalil proyeksi pada segitiga tumpul dan dalil proyeksi pada segitiga lancip.

a. Dalil Proyeksi Segitiga Tumpul

Pada segitiga tumpul ABC, garis BC diproyeksikan dengan garis AB menghasilkan garis DA. Panjang DA dapat dicari dengan menggunakan dalil proyeksi pada segitiga tumpul yaitu sebagai berikut: 

b. Dalil Proyeksi Segitiga Lancip

Tidak jauh berbeda dengan dalil proyeksi segitiga tumpul, pada segitiga lancip ABC, garis CA diproyeksikan dengan garis AB menghasilkan garis AD, sehingga panjang AD dapat dicari menggunakan dalil proyeksi pada segitiga lancip yaitu sebagai berikut:

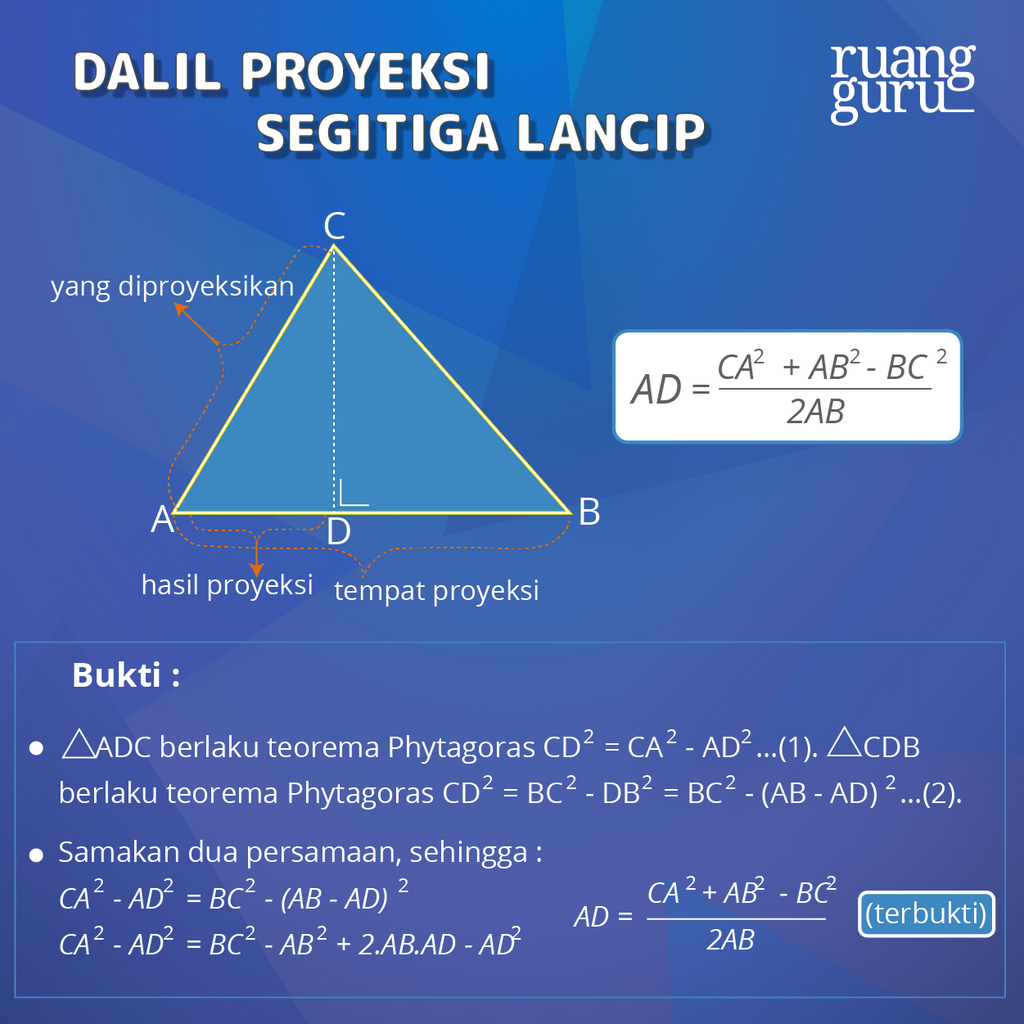
3. Dalil Stewart

Coba kamu perhatikan gambar di bawah ini. Segitiga sembarang ABC dengan sebuah garis sembarang, yaitu CD yang menghubungkan satu titik sudut dengan sisi dihadapannya. Kira-kira, dapatkah kamu menghitung panjang CD? Hmm… Biasanya sih kalau kita disuruh mencari panjang salah satu sisi segitiga sembarang, kita bisa menggunakan aturan sinus atau cosinus, ya. Tapi, nggak hanya dua aturan itu saja, Squad. Kita juga bisa menggunakan dalil segitiga yang satu ini. Yap! Dalil stewart.

Pada dasarnya, dalil stewart menyatakan hubungan antara sisi-sisi segitiga dengan panjang ruas garis yang ditarik dari titik sudut segitiga dengan sisi dihadapannya. 

4. Dalil Menelaus

Jika diberikan sebuah segitiga ABC, titik D terletak pada garis CA dan titik E terletak pada garis BC, sehingga terbentuk ruas garis DE. Garis AB dan DE diperpanjang sehingga keduanya berpotongan di titik F, seperti gambar di bawah. Maka, titik D, E, dan F akan segaris (kolinear) dan berlaku dalil Menelaus sebagai berikut: 

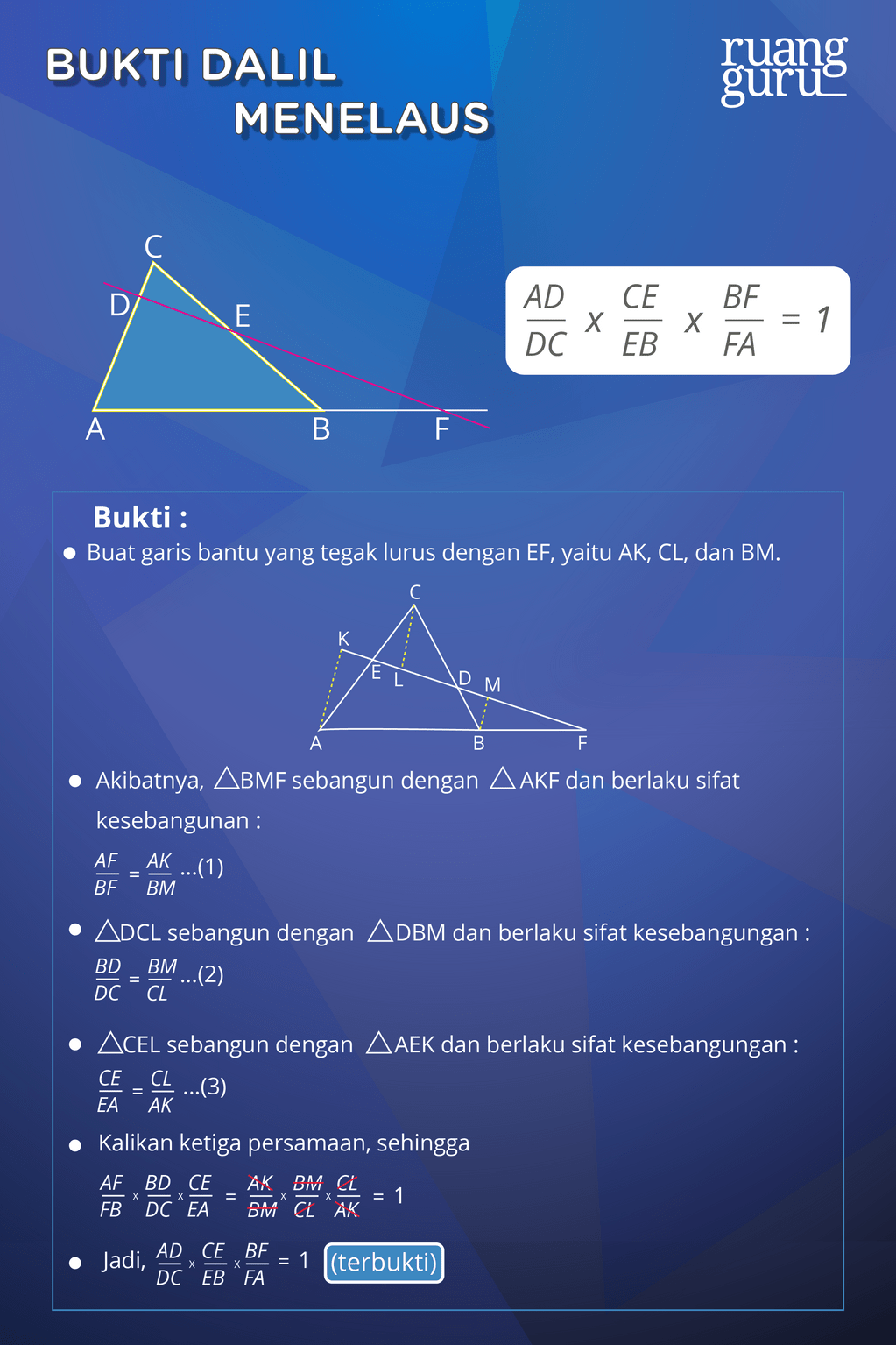
Wah, banyak juga ya dalil-dalil yang berkaitan pada segitiga. Tapi sebenarnya, gunanya dalil-dalil ini untuk apa, sih? Bukan untuk bikin kepala kita jadi tambah pusing, kan? Hehe… 

Eits, tentu saja tidak, Squad. Sudah pasti, dalil-dalil ini bisa kamu gunakan untuk membantumu dalam menyelesaikan soal Matematika yang berkaitan dengan segitiga. Selain itu, dalil-dalil ini juga bisa digunakan untuk membantu dalam pembuktian rumus. Contohnya saja dalil stewart yang dapat dibuktikan menggunakan dalil proyeksi, atau rumus-rumus lain yang berkaitan juga bisa dibuktikan menggunakan dalil-dalil ini. Jadi, kamu harus tetap pahami, ya.

Squad, segitiga memang istimewa, ya! Sekarang, kamu nggak hanya tahu cara menghitung luas atau keliling segitiga saja, nih. Tapi juga macam-macam garis istimewa dan dalil pada segitiga. Nah, kalau kamu merasa artikel ini kurang lengkap untuk menjawab rasa keingintahuanmu terhadap materi segitiga, kamu bisa lho belajar lebih lanjut lewat aplikasi ruangbelajar. Kini, ruangbelajar juga tersedia untuk PC atau laptop kamu. Belajar jadi lebih nyaman dengan layar yang lebih besar. Tunggu apa lagi? Yuk, buruan daftar!