Latihan Soal Penilaian Akhir Semester 2019 Matematika Kelas 9

Artikel ini berisi kumpulan soal latihan untuk Penilaian Akhir Semester (PAS) ganjil kelas 9 untuk pelajaran matematika

—

Mendekati masa-masa ujian kayak gini, sebagai murid, pasti ada dong perasaan deg-degan. Walaupun udah belajar setiap hari, tapi tetap aja, yang namanya kata “ujian” bikin kita khawatir. Ujian sekolah, ujian SIM, ujian ujianan soire soire sampia pusiang. Apalagi kamu anak kelas 9 yang sebentar lagi bakalan naik jenjang ke SMA. Oleh karena itu, kita butuh yang namanya latihan. Paling tidak, dengan latihan kita bisa mengukur bagian mana dari materi yang udah kita kuasai atau belum. Setelahnya, tinggal kita tingkatin deh materi yang belum kita pahamin.

Berikut adalah kumpulan soal latihan untuk Penilaian Akhir Semester (PAS) yang bisa kamu coba:

 

 

1) Topik: Bilangan Berpangkat

Subtopik: Pengertian bilangan berpangkat

 

Perkalian 3 X 3 X 3 X 3 X 3 jika dituliskan dalam bentuk pangkat menjadi….
A. 3^-5
B. 5^-3
C. 3⁵
D. 5³

 

 

Jawaban: C

Pembahasan

Dalam bentuk pangkat, yaitu:

3 X 3 X 3 X 3 X 3 = 3⁵

2) Topik: Bilangan Berpangkat – Eksponen

Subtopik: Sifat bilangan berpangkat I

 

Sebuah kubus memiliki sisi 4k satuan. Perbandingan luas permukaan dan volume kubus tersebut adalah….

A. 1 : 2k
B. 2 : k
C. 2 : 3k
D. 3 : 2k

 

Jawaban: D

Pembahasan:

Sisi kubus (s) = 4k

Luas permukaan kubus (L) = 6s²

Volume Kubus (V) = s³

Maka,

 

Jadi, perbandingan luas permukaan dan volume kubus tersebut adalah 3 : 2k

3) Topik: Bilangan Berpangkat – Eksponen

Subtopik: Persamaan bilangan berpangkat I

 

Nilai x yang memenuhi persamaan 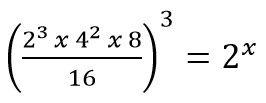 adalah …

A. 9
B. 12
C. 18
D. 36

 

 

Jawaban: C

Pembahasan:

Ingat bahwa a^m x aⁿ = am + n, (a^m)ⁿ = a^m x n, a^m/aⁿ = a^m-n maka

 

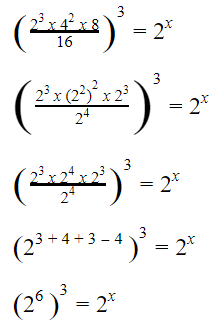
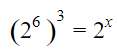
Jadi, nilai x yang memenuhi persamaan tersebut adalah 18.

4) Topik: Bentuk Akar

Subtopik: Penjumlahan dan pengurangan bentuk akar

 

Hasil dari 6√2 +4√8 – 3√32 adalah …

A. 2√2
B. 3√2
C. 5√2
D. 7√2

 

 

Jawaban: A

Pembahasan:

 

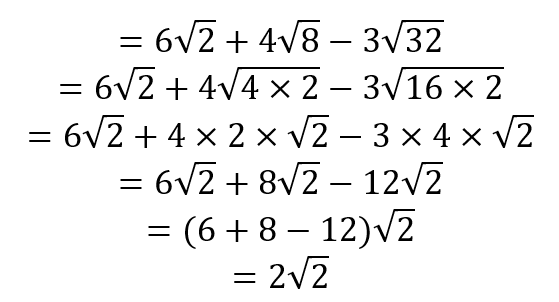
Jadi, hasil dari 6√2 +4√8 – 3√32 adalah 2√2

.

5) Topik: Bentuk Akar

Subtopik: Pembagian bentuk akar

 

Hasil dari √1350 ÷ √3 adalah….

A. 5√2
B. 5√3
C. 15√2
D. 15√3

 

Jawaban: C

Pembahasan:

 

 

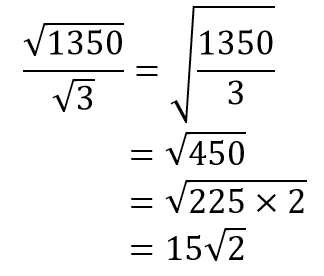
6) Topik: Bentuk Akar

Subtopik: Rasional bentuk akar

 

Bentuk sederhana dari 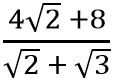adalah…

A. 2(√6+2√3+2√2-2)
B. 4(√6-2√3+2√2+2)
C. 2(√6-2√3-2√2+2)
D. 4(√6+2√3-2√2-2)

 

Jawaban: D

Pembahasan:

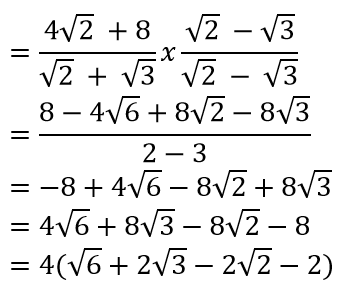
7) Topik: Logaritma

Subtopik: Sifat Logaritma

 

Diketahui ²log a =1/2 dan ³log b =1/3. Jika x = a² dan y = b³, maka ^xlog y =…

A. ³log12
B. ²log 12
C. ³log 2
D. ²log 3

 

Jawaban: D

Pembahasan:

Ingat, Bentuk umum logaritma!

Maka:

²log a =1/2↔2^1/2 = a↔a = √2

dan

³log b =1/3 ↔ 3^1/3 = b ↔ b = ³√3 

Karena

x = ²√2 = 2 

dan

y = b³

y = (³√3)³ = 3

Sehingga:

^xlog y = ²log 3

Baca juga: Latihan Penilaian Akhir Semester 2019 Bahasa Indonesia Kelas 10 

8) Topik: Logaritma

Subtopik: Persamaan logaritma

 

Jika persamaan  ^x log 3 + ^x log (3x-6) = 2 memiliki akar-akar x₁ dan x₂ dengan x₁ > x₂, maka x₁ – x₂ adalah…

 

A. 1
B. 2
C. 3
D. 4

Jawaban: C

Pembahasan:

 ^x log 3 + ^x log (3x-6) = 2

 ^x log (3(3x-6)) = ^x log x²

 ^x log (9x-18) = ^x log x²

9x -18 = x²

x² – 9x + 18 = 0

(x – 6) (x – 3) = 0

x₁ = 6   x₂ = 3

karena akar-akar x₁ dan x₂ dengan x₁ > x₂ maka

x₁-x₂

= 6-3

= 3

9) Topik: Logaritma

Subtopik: Persamaan logaritma

 

Nilai x yang memenuhi persamaan   (²log x)² – 5 ²log x +6=0  adalah ….

A. x = 4 atau x = 9
B. x = 2 atau x = 8
C. x = 4 atau x = 8
D. x = 2 atau x = 9

 

Jawaban: C

Pembahasan:

misalkan:  ²log x = y

Persamaan tersebut dapat ditulis sebagai:

10) Topik: Persamaan Kuadrat

Subtopik: Faktorisasi pada persamaan kuadrat

 

Salah satu akar-akar dari persamaan kuadrat 3x² + 8x – 35 = 0 adalah ….

A. 5
B. 7
C. 5/3
D. 7/3

 

Jawaban: D

Pembahasan:

 

3x² + 8x – 35 = 0 (faktor dari 35 adalah 1 dan 35 atau 5 dan 7), maka:

• (3x – 1) (x + 35) = 0 (-1 dan 105 di jumlahkan menjadi 104 (salah))
• (3x – 7) (x + 5) = 0 (15 dan -7 di jumlahkan menjadi 8 (benar)

Jadi, (3x – 7) (x + 5) = 0

x = 7/3 | dan x = -5

• Jadi, salah satu akar-akar dari persamaan kuadrat 3x² + 8x – 35 = 0 adalah 7/3

11) Topik: Persamaan Kuadrat

Subtopik: Jumlah, hasil kali, dan selisih akar persamaan kuadrat

 

Diketahui persamaan 2x² = – 6x – 8 memiliki penyelesaian p dan q maka nilai dari 1/p² + 1/q² adalah ….

A. 1/8
B. 1/16
C. 8
D. 16

 

 

Jawaban: B

Pembahasan:

Karena p dan q merupakan penyelesaian, maka ia juga termasuk dari akar-akar persamaan kuadrat 2x² + 6x + 8 = 0

Ingat kembali rumus:

p + q = – (b/a) = -3

pq = c/a = 4

Sehingga;

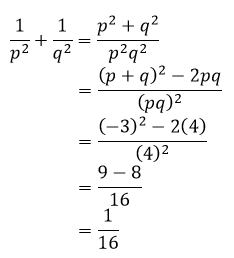
12) Topik: Persamaan Kuadrat

Subtopik: Menyusun persamaan kuadrat baru

 

Persamaan kuadrat 2x² – 2x + a – 1 = 0 mempunyai dua akar real berlawanan tanda, maka nilai a yang memenuhi adalah ….

A. a > 1.5
B. a < 1.5
C. a > 3
D. a < 3

Jawaban: B

Pembahasan:

Dari persamaan kuadrat 2x² – 2x + a – 1 = 0 di mana (a = 2, b = -2, c = a-1), maka:

Syarat akar real berlawanan tanda :

• x₁x₂ < 1

x₁ . x₂ < 1 c/a < 1

(a-1)/2 < 1

a-1 < 2

a < 3 … (1)

 

• D >0

b² – 4ac > 0

(-2)² – 4 (2) (a-1) > 0

4 – 8a + 8 > 0

12 > 8a

a < 12/8

a < 1.5 … (2)

Dengan mengiris persamaan (1) dan (2), didapat bahwa a < 1.5

13) Topik: Fungsi Kuadrat

Subtopik: Grafik fungsi kuadrat

 

Berikut ini yang benar mengenai grafik fungsi f(x)=-3x² – x – 5 adalah…

A. Grafik terbuka ke atas
B. Titik puncak kurva ada di kiri sumbu Y
C. Grafik memotong sumbu X di 2 titik
D. Titik potong dengan sumbu Y ada di atas sumbu X

 

 

Jawaban: B

Pembahasan:

 

Dari sini, didapat bahwa:

 

a < 0, maka grafik terbuka ke bawah
a dan b tandanya sama, maka titik puncaknya di kiri sumbu Y
c < 0 maka titik potong dengan sumbu Y ada di bawah sumbu X
D < 0 maka grafik tidak memotong sumbu X

Jadi, opsi yang benar adalah opsi B.

14) Topik: Fungsi Kuadrat

Subtopik: Membuat fungsi kuadrat

Persamaan fungsi kuadrat yang melalui titik puncak (3, 4) dan titik lain di titik (2,3) adalah….

A. f(x) = x² – 6x + 5
B. f(x) = -x² + 6x – 5
C. f(x) = x² – 4x – 5
D. f(x) = -x² + 4x – 5

Jawaban: B

Pembahasan:

Persamaan grafik fungsi kuadrat yang melalui titik puncak (x_p, y_p) dan titik lain (x, y) yaitu :

y = a(x – x_p)² + y_p

maka persamaan fungsi kuadrat yang melalui titik puncak (3,4) dan titik lain (2,3), yaitu :

3 = a(2 – 3)² + 4

-1 = a(1) ↔ a = -1

Sehingga persamaan fungsi kuadrat tersebut adalah :

f(x) = -1(x – 3)² + 4

f(x) = -1(x² – 6x + 9) + 4

f(x) = -x² + 6x – 5

15) Topik: Fungsi Kuadrat

Subtopik: Aplikasi fungsi kuadrat

 

Sebuah roket diluncurkan ke atas yang lintasannya membentuk grafik fungsi kuadrat dengan persamaan h(t) = t² + 6t + 18. Tinggi maksimum yang dicapai roket tersebut adalah….

A. 8 meter
B. 9 meter
C. 10 meter
D. 11 meter

 

 

Jawaban: B

Pembahasan:

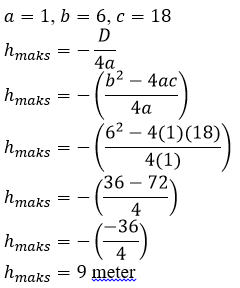
16) Topik: Transformasi Geometri

Subtopik: Translasi, refleksi

 

Sebuah titik A (2,3) ditranslasikan sejauh (a, b), lalu direfleksikan terhadap sumbu -X mempunyai bayangan di titik A’ (4, -4). Nilai dari a + b…

A. 1
B. 2
C. 3
D. 4

 

 

Jawaban: C

Pembahasan:

Ingat bahwa translasi sebuah titik, yaitu:

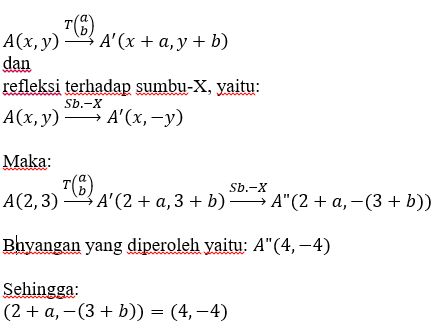
diperoleh:

2 + a = 4a = 4 – 2a = 2

dan

-(3 + b) = -43 + b = 4b = 4 – 3b = 1

Jadi, nilai

a + b

17) Topik: Transformasi Geometri

Subtopik: Rotasi

 

Titik (3, -7) dirotasi 90^o searah jarum jam dengan pusat rotasi adalah (1, 5), maka bayangan titik tersebut adalah…

A. (-11, 4)
B. (-11, 1)
C. (-11, 3)
D. (11, -2)

Jawaban: C

Pembahasan:

Pertama, translasikan dulu pusatnya ke (0, 0) yaitu (-1, -5).

Titiknya harus ditranslasikan dengan arah yang sama, sehingga titik setelah di translasikan adalah ( 3 + (- 1), -7+ (- 5) ) = (2, -12)

Bayangan titik setelah di rotasi 90^o searah jarum jam adalah (y, -x). Maka bayangan titiknya adalah (12, -2).

Setelah itu kembalikan ke titik asal (-12 + 1, -2 + 5) = (-11, 3)

18) Topik : Transformasi Geometri

Subtopik : Rotasi, Dilatasi

 

Titik A (a, b) dirotasikan berlawanan arah jarum jam dengan pusat O (0, 0) sejauh 90^o dan dilanjutkan dengan dilatasi dengan pusat O (0, 0) dan faktor skala 2 yang menghasilkan bayangan A” (6, 4). Koordinat titik A adalah ….

A. (3, -2)
B. (-2, 3)
C. (2, -3)
D. (-3, 2)

Jawaban: C

Pembahasan:

Ingat bahwa rotasi terhadap pusat O(0, 0) berlawanan arah jarum jam sejauh 90^o, yaitu:

A (x, y)  R(O, 90°) →  A’ (-y, x)

dan

Dilatasi terhadap pusat O(0, 0) dengan faktor skala k, yaitu:

A (x, y) D(O, k)→ A’ (kx, ky)

Maka:

A (a, b) R(O, 90°) → A’ (-b, a) D(O,2) →A”(-2b, 2a)

Bayangan yang diperoleh yaitu: A” (6, 4)

Sehingga:

(-2b, 2a) = (6, 4)

diperoleh:

-2b = 6 ↔ b = -3

dan

2a = 4 ↔ a = 2

Jadi, koordinat titik A adalah (2, -3)

19) Topik: Kongruen dan Kesebangunan

Subtopik: Kesebangunan dua bangun

Perhatikan gambar di bawah ini!

 

 

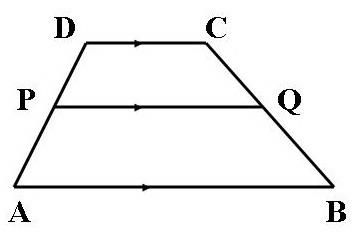
Gambar trapesium ABCD dengan PQ//AB. Jika diketahui DP = 5 cm, AP = 3 cm dan CQ = 7,5 cm, maka panjang QB = …

A. 4,5 cm
B. 7,5 cm
C. 9 cm
D. 12 cm

Jawaban: A

Pembahasan:

20) Topik: Kongruen dan Kesebangunan

Subtopik: Segitiga sebangun

 

Perhatikan gambar berikut!

 

 

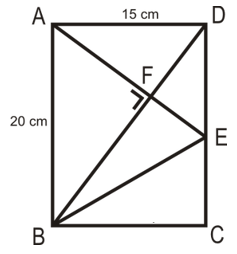
Luas trapesium ABED adalah….

A. 1875/8 cm²
B. 1875/16 cm²
C. 1875/32 cm²
D. 1875/64 cm²

 

Jawaban: A

Pembahasan:

 

 

Dengan kesebangunan segitiga ABD dan segitiga DAE akan diperoleh:

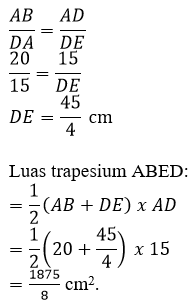
Nah, dari kedua puluh soal untuk latihan Penilaian Akhir Semester (PAS) matematika kelas 9 ini, mana yang belum kamu kuasai? Coba, latihan lagi sebelum menyesal. Kalau kamu ingin memahami konsepnya lagi, tonton aja materinya di ruangbelajar!