Turunan Fungsi Aljabar: Konsep Rumus, Aturan Rantai & Contoh | Matematika Kelas 11

Pada artikel Matematika kelas 11 ini, kamu akan belajar konsep, rumus, dan cara mencari turunan fungsi aljabar, disertai dengan contoh soalnya. Yuk, simak!

—

Halo, guys! Hani di sini, dan ini adalah…

Heheheheh…

Oke, gimana kabarnya, guys? Di artikel kali ini, aku mau bahas materi tentang turunan. Bukan, bukan turunan yang ada di bayangan kamu.

Meluncur tanpa batas dan melampauinya~~~ (Sumber: giphy.com)

Tapi, turunan yang aku maksud adalah turunan fungsi. Materi ini ada kaitannya dengan limit fungsi dan kemiringan (gradien) garis di suatu titik yang sebelumnya sudah kamu pelajari.

Nah, menurut definisinya, turunan fungsi di suatu titik adalah gradien garis singgung fungsi di titik tersebut. Hmm, maksudnya gimana, sih? Oke, kita pahami konsep turunan fungsinya dulu, ya.

Konsep Turunan Fungsi

Coba kamu perhatikan grafik fungsi di bawah ini.

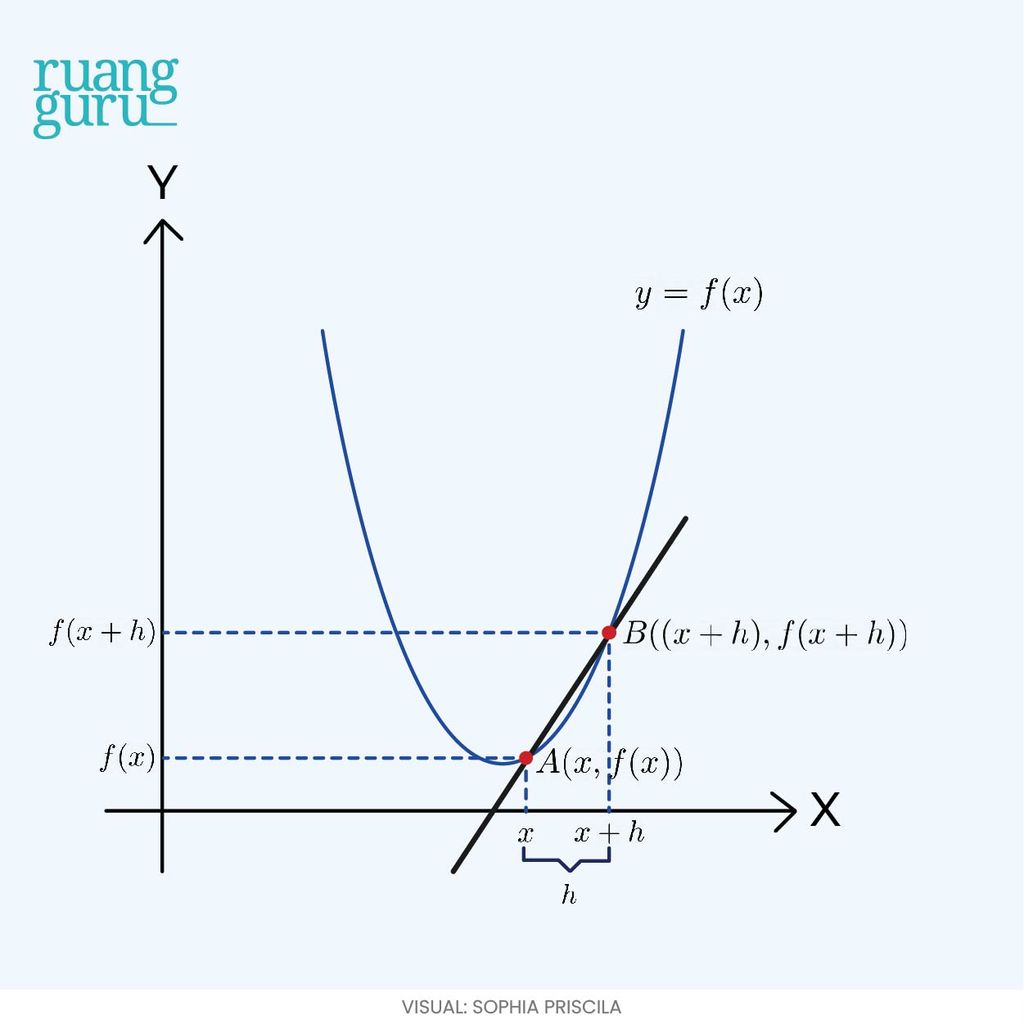
Misalkan, grafik di atas merupakan grafik fungsi kontinu f(x). Lalu, terdapat garis lurus yang memotong kurva f(x) di dua titik, yaitu titik A dan B. Nah, karena memotong kurva di dua titik, garis lurus ini bisa kita sebut sebagai garis secan atau garis AB.

Kalo kita lihat pada gambar, garis AB pasti punya kemiringan (gradien) tertentu, nih. Kamu masih ingat kan, cara mencari gradien garis lurus? Gradien garis lurus bisa kita cari menggunakan rumus berikut ini:

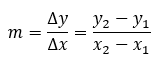
Nah, karena titik absis (koordinat x) dan ordinatnya (koordinat y) sudah diketahui, bisa kita masukkan deh ke dalam rumus. Sehingga, diperoleh gradien garis AB nya seperti ini.

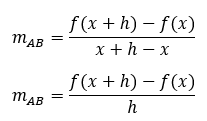
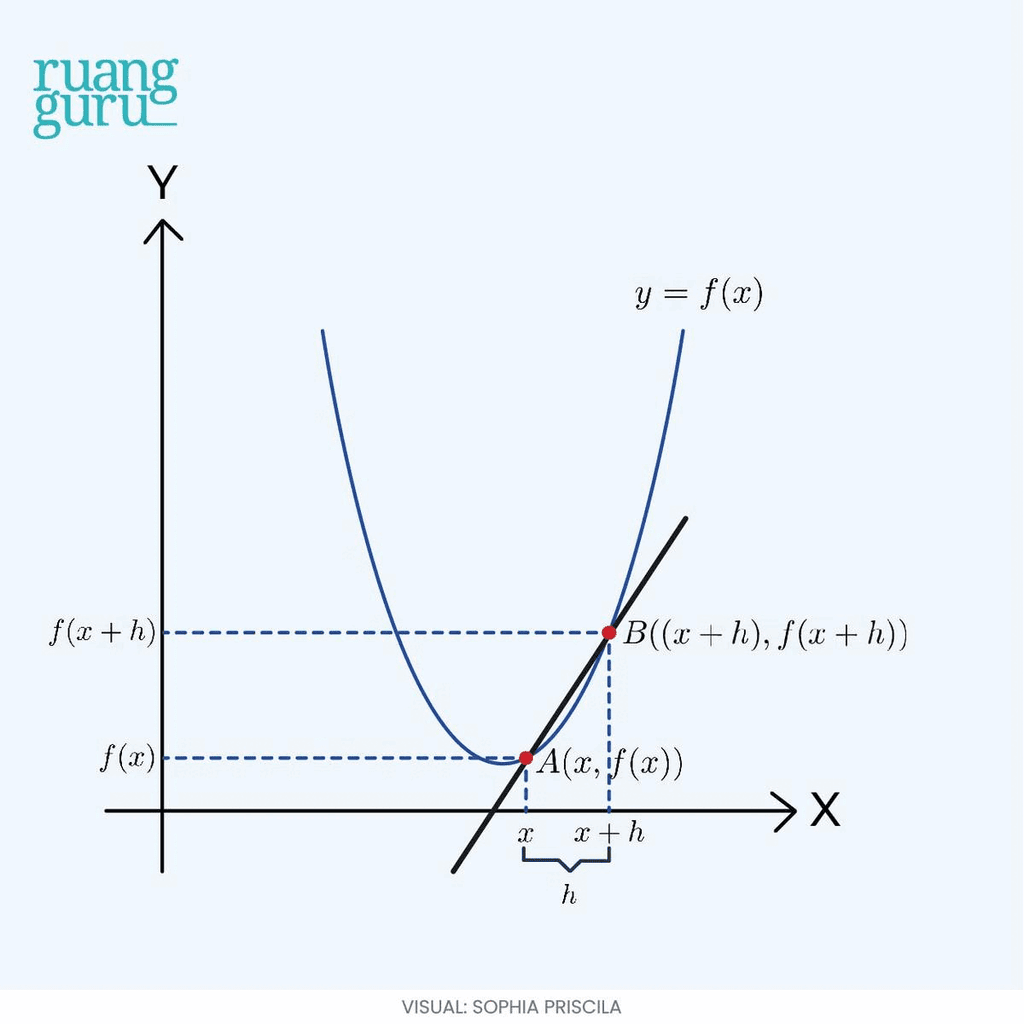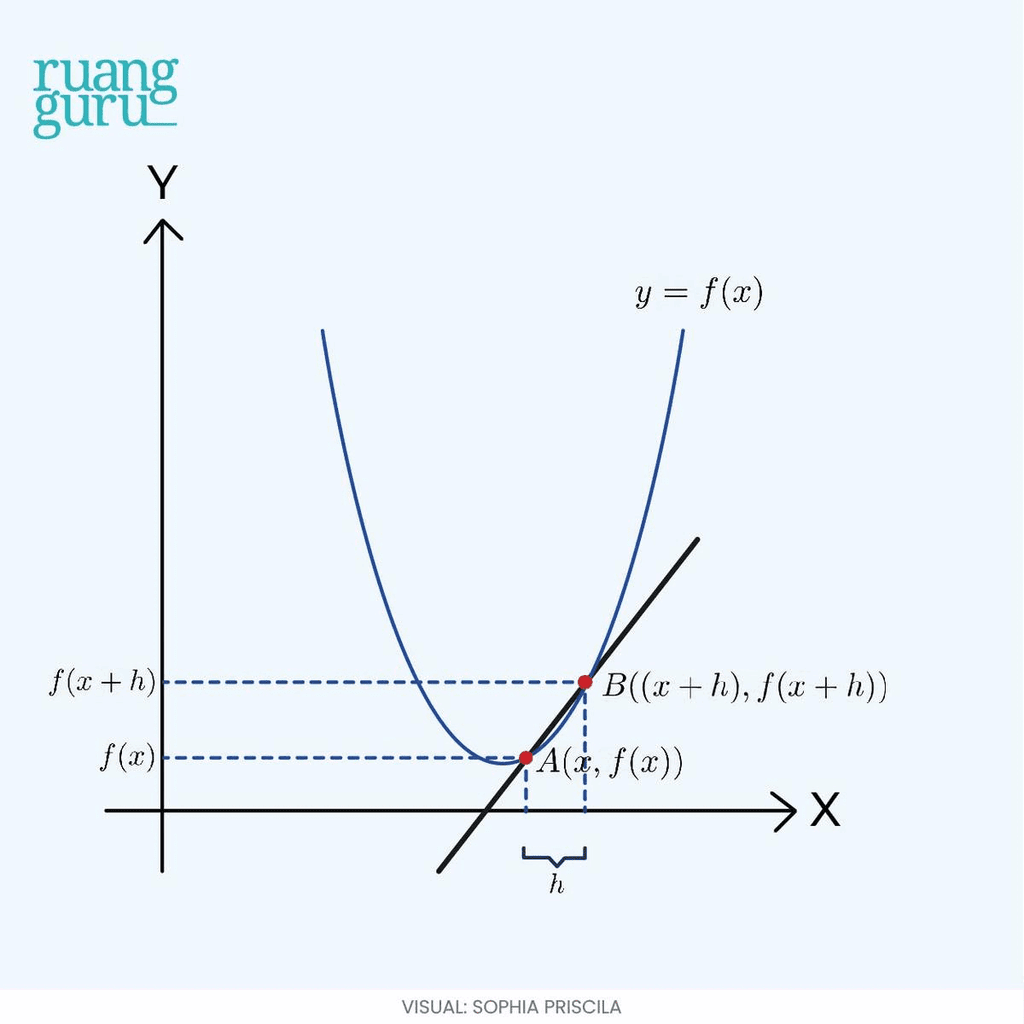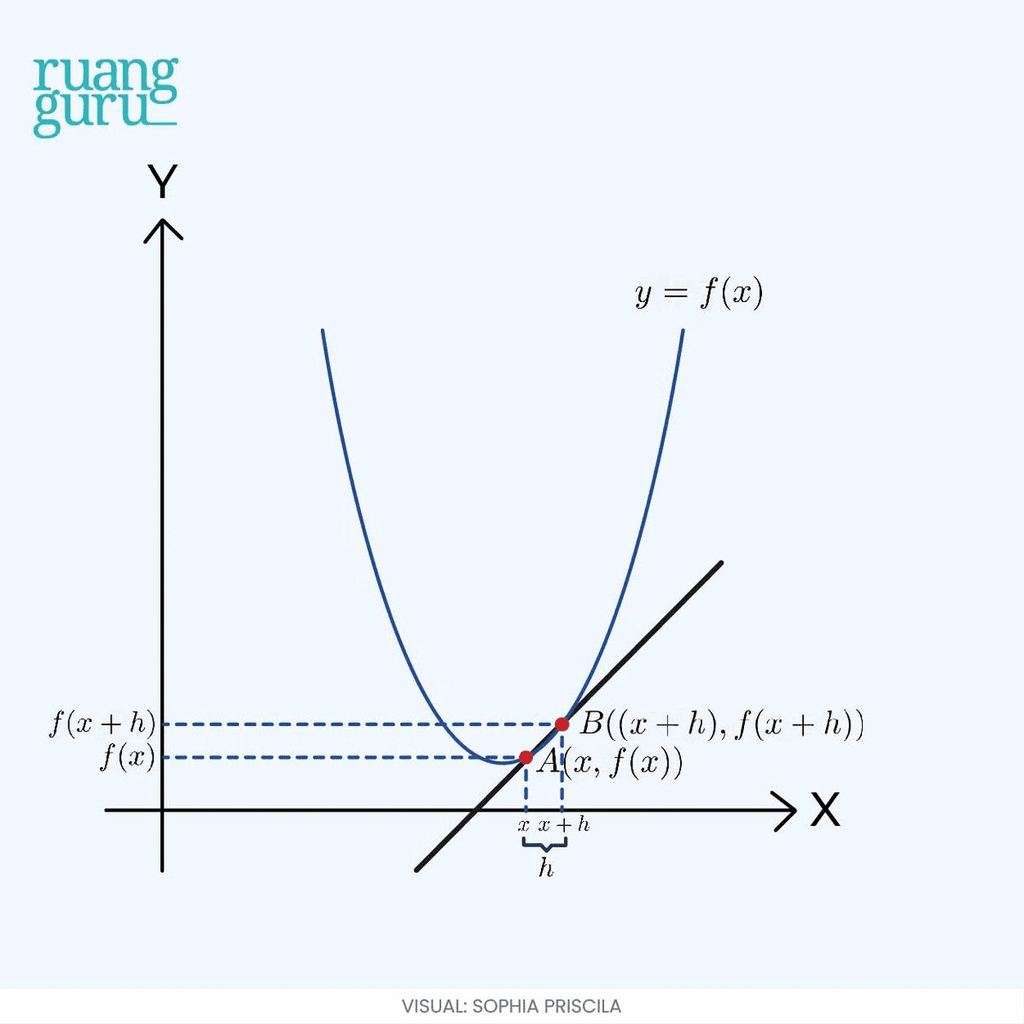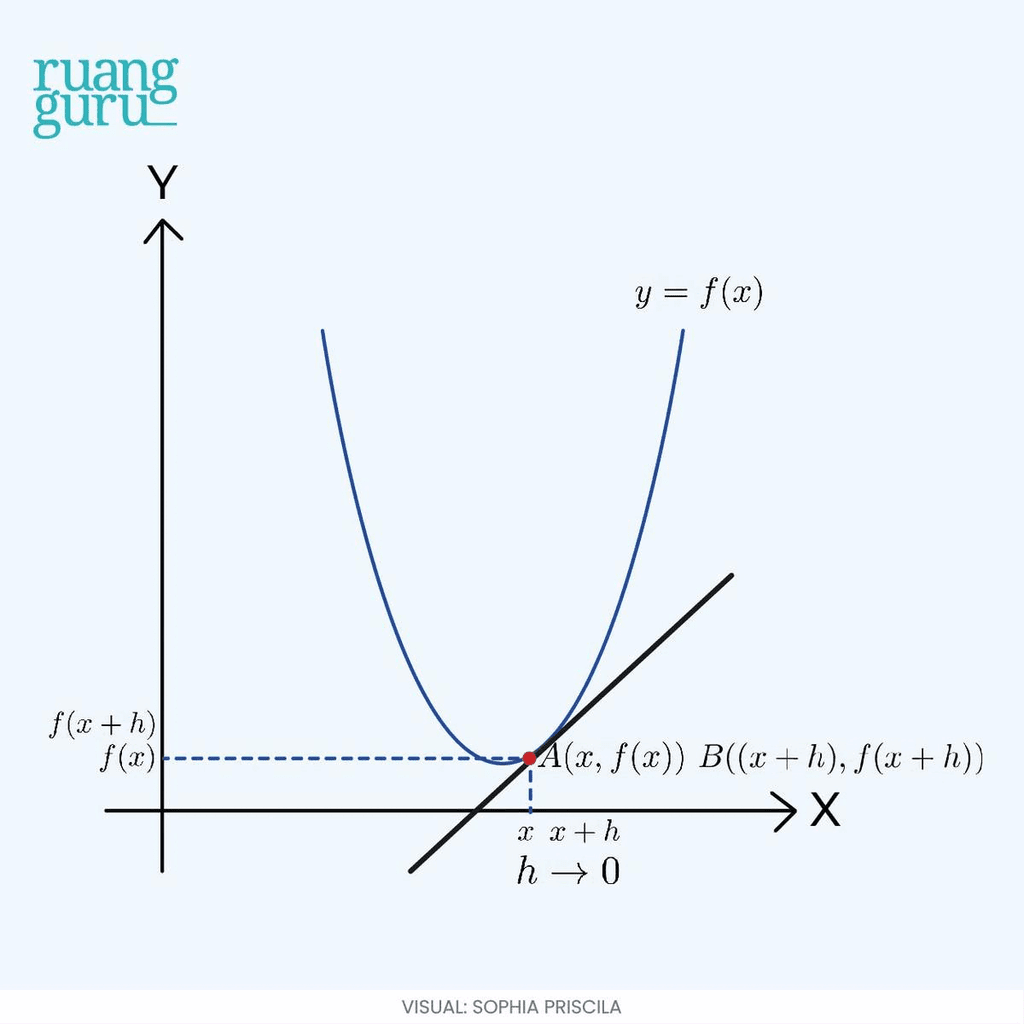
Sekarang, kalo misalnya titik A dan B ini kita geser agar saling berdekatan satu sama lain, hingga jarak antar titiknya (h) mendekati nol, kira-kira apa yang bakal terjadi?

Salah, mereka nggak jadian. 🙁

Garis AB yang awalnya memotong kurva di dua titik, lama-kelamaan berubah menjadi garis yang tampak menyinggung kurva di satu titik aja. Garis singgung ini kemudian bisa kita sebut sebagai garis tangen.

Untuk gradien garisnya, tetap sama, guys. Tapi, karena nilai h nya mendekati nol, jadi kita gunakan konsep limit.

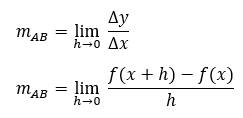
Dengan syarat, nilai limitnya ada, ya. Nah, gradien garis singgung inilah yang disebut turunan fungsi. 

Gimana, paham ya dengan konsep turunan?

Baca Juga: Mengenal Matriks dalam Matematika: Pengertian, Jenis, dan Transpose

Rumus Turunan Fungsi Aljabar

Jika kita punya fungsi y = f(x), maka f’(x) atau y’ merupakan notasi turunan pertama fungsi tersebut. Kamu juga bisa menggunakan notasi lain, seperti 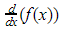atau 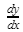. Sementara itu, turunan pertama fungsi aljabar dirumuskan sebagai berikut:

Nah, supaya kamu lebih paham, kita masuk ke contoh soal aja, ya.

Contoh Soal

Tentukan turunan pertama fungsi berikut ini:

1. f(x) = 2
2. f(x) = 3x
3. f(x) = x²

Pembahasan:

1. Pada fungsi f(x) = 2, kalo digambarkan dalam bentuk grafik, maka akan seperti ini:

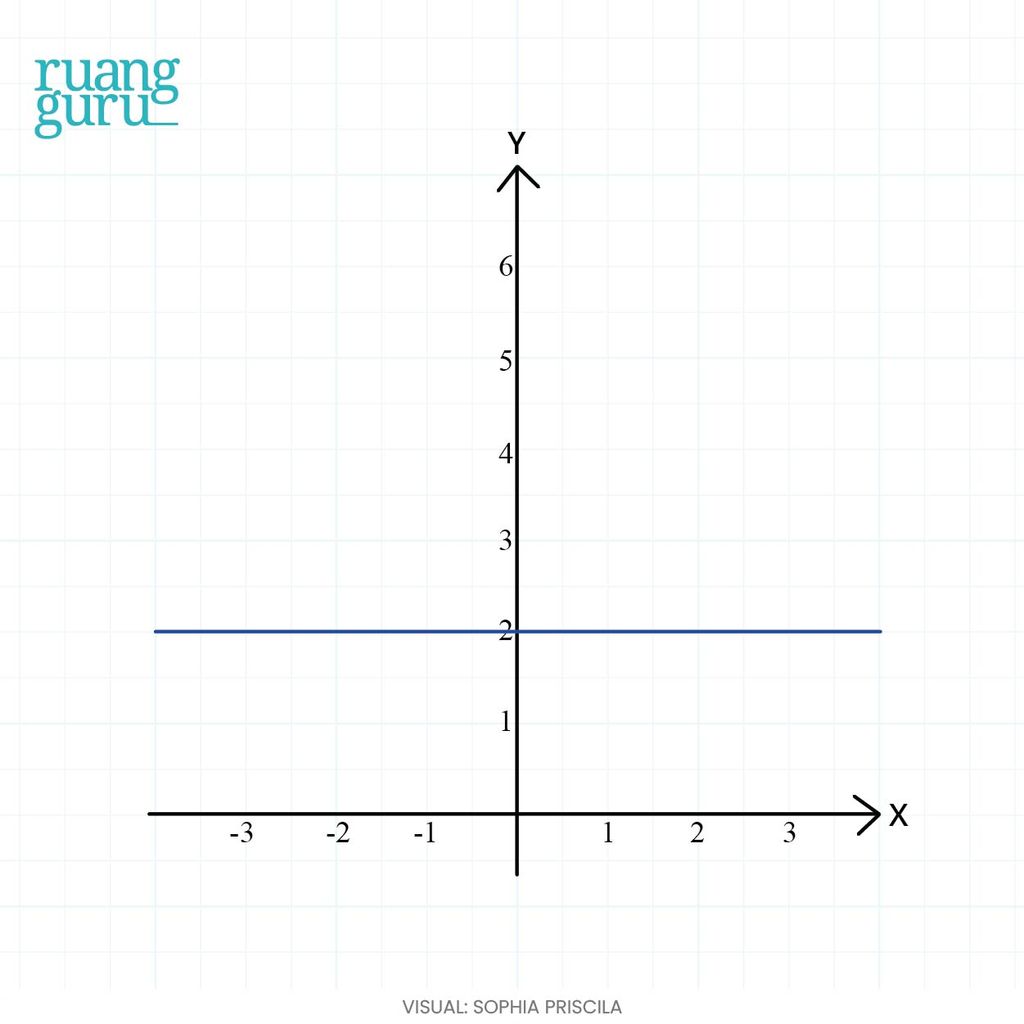
Ingat definisi turunan, ya! Turunan fungsi di suatu titik adalah gradien garis singgung fungsi di titik tersebut. Sekarang, coba kita cari turunan fungsi f(x) = 2 jika dilihat dari bentuk grafiknya.

Fungsi f(x) = 2 merupakan fungsi konstan. Oleh karena itu, grafiknya berupa garis yang sejajar dengan sumbu x di titik x = 2. Jadi, datar gitu ya garisnya.

Nah, karena grafik fungsinya datar, otomatis garis singgung fungsi tersebut juga ikutan datar dong. Alhasil, garis singgung fungsi f(x) = 2 nggak punya kemiringan (nilai gradiennya = 0). Berarti, turunan pertama fungsi f(x) = 2 adalah nol.

Coba kita buktikan menggunakan rumus turunan di atas, ya. Karena dia fungsi konstan, maka f(x + h) = f(x), yaitu 2. Sehingga,

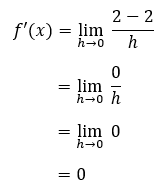
Jawabannya sama ya dengan analisis kita sebelumnya. Dengan begitu, bisa dipastikan nih, jika f(x) = C (fungsi konstan), maka f’(x) = 0. Lanjut ke soal berikutnya~

2. Ada yang bisa menebak nggak, kira-kira fungsi f(x) = 3x kalo digambarkan akan seperti apa? Nah, karena f(x) = 3x merupakan fungsi linear, maka grafiknya berupa garis lurus, tapi nggak sejajar dengan sumbu x maupun y. Gambarnya, bakal kayak gini:

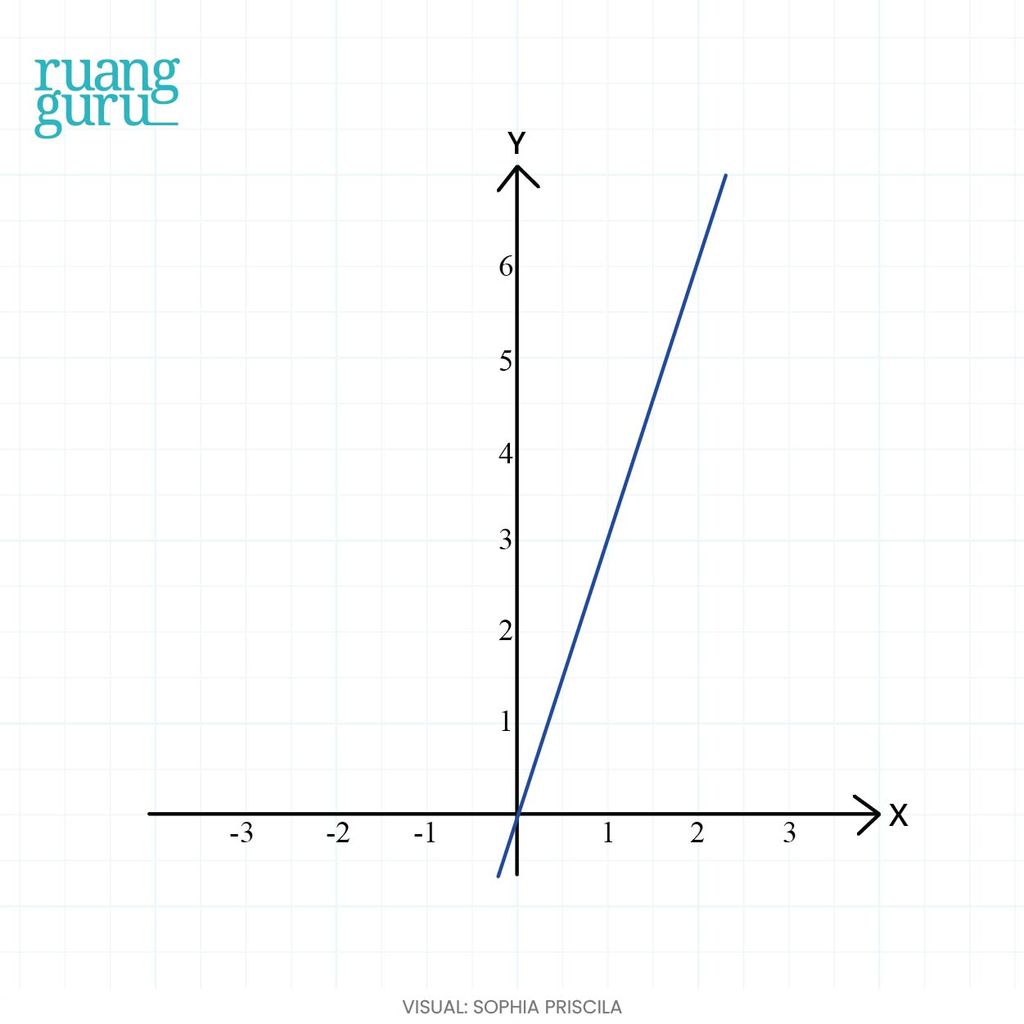
Sama seperti poin a, garis singgung fungsi tersebut akan mengikuti bentuk grafik fungsinya. Oleh karena itu, gradien garis singgung fungsi tersebut juga akan sama dengan gradien grafik fungsinya.

—

Intermezo sebentar, yuk! Bingung cari kumpulan latihan soal yang bisa bantu kamu meningkatkan pemahaman materi? Cobain fitur Bank Soal dari Ruangguru aja. Kini, Bank Soal dilengkapi dengan berbagai fungsi yang kece dan menarik, lho! Klik banner di bawah untuk cari tahu!

Kita lanjut ke materi ya. Kamu masih ingat nggak dengan bentuk persamaan y = mx + c? Artinya, gradien suatu persamaan linear adalah koefisien dari variabel x itu sendiri, yaitu m.

Nah, f(x) = 3x ini kan merupakan persamaan linear. Berarti, gradien garisnya adalah koefisien x, yaitu 3. Berarti, gradien garis singgungnya juga 3. Jadi, turunan pertama fungsi f(x) = 3x adalah 3. Coba ya kita buktikan lagi menggunakan rumus turunannya.

f(x) = 3x, maka f(x + h) = 3(x + h). Sehingga,

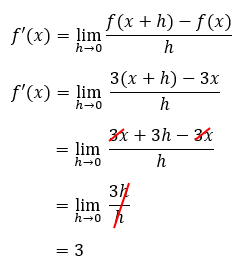
Nah, variabel h di bagian penyebut ini bisa kita coret karena nilainya nggak nol ya, guys. Dan ternyata hasilnya sama juga nih dengan analisis kita. Berarti, kalo ada f(x) = ax (fungsi linear), maka f’(x) = a.

Oke, guys, sampai sini, semoga kamu bisa semakin paham dengan maksud definisi turunan dan cara mencari nilai turunan pertama suatu fungsi. Sekarang, kita lanjut ke soal yang terakhir.

3. Diketahui, g(x) = x² adalah fungsi kuadrat. Bentuk kurvanya melengkung ke atas, ya. Karena garisnya melengkung, maka garis singgungnya kurang lebih bakal kayak gini:

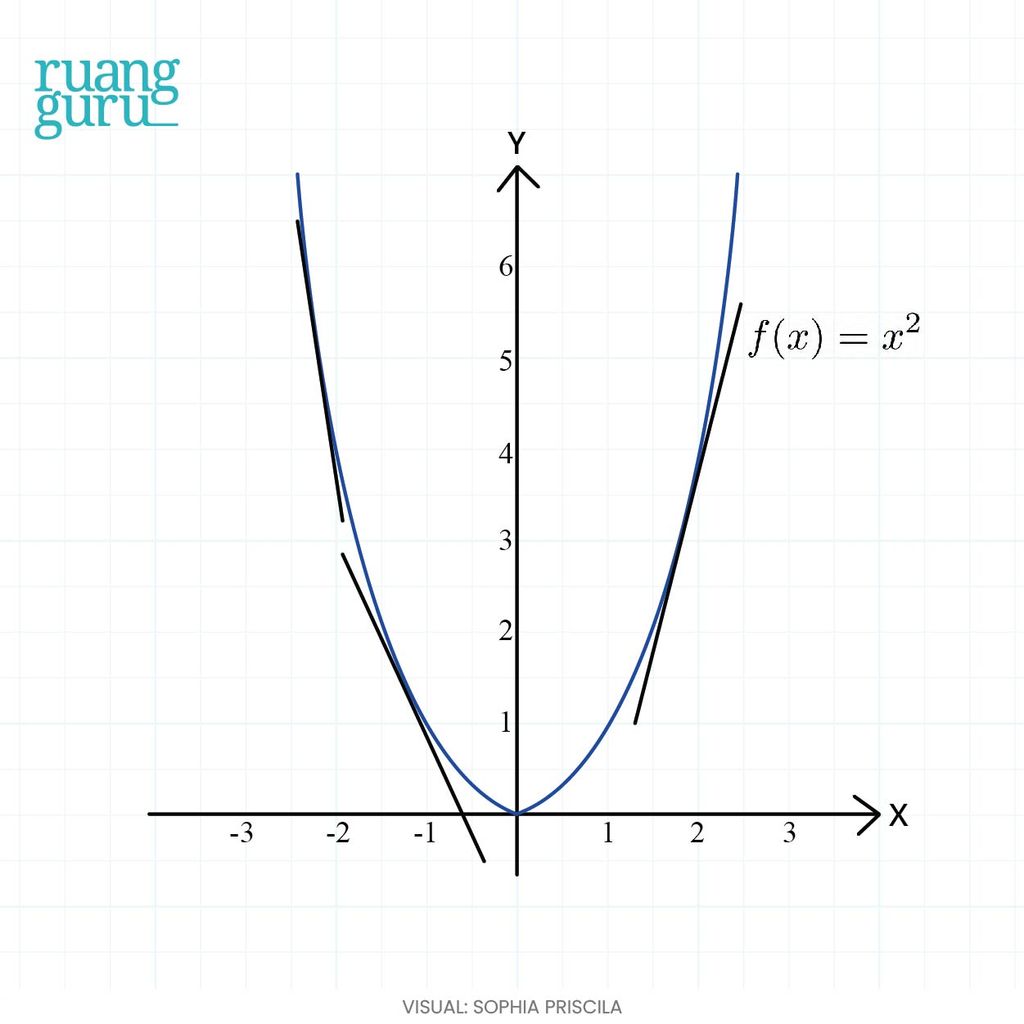
Ketiga garis singgung tersebut cuma contohnya aja, ya. Sebenarnya, garis singgungnya itu ada di sepanjang kurva. Nah, nggak kayak dua contoh sebelumnya, untuk fungsi kuadrat ini agak sulit untuk menganalisis turunan fungsinya berdasarkan kurva. Soalnya, gradien garis singgungnya juga berbeda-beda di setiap titik. Jadi, langsung aja ya kita cari turunannya menggunakan rumus.

f(x) = x², maka f(x + h) = (x + h)². Sehingga,

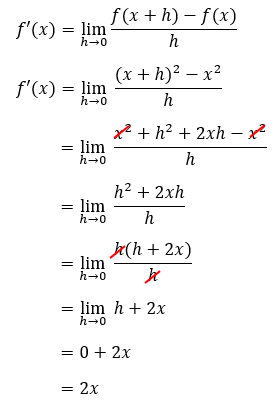
Jadi, kalo misalnya kamu diminta untuk mencari turunan pertama fungsi f(x) = x² di titik x = 2, tinggal substitusi aja nilai x ke dalam f’(x) = 2x. Jawabannya, f’(2) = 2.2 = 4.

Mudah nggak sih, guys? Hmm, kalo dilihat dari ketiga contoh soal di atas sih, masih mudah-mudah aja, ya. Tapi, gimana kalo kamu diminta untuk mencari turunan pertama fungsi f(x) = x²⁰²¹? Hayoloh?!

Rumus Turunan Fungsi Aljabar untuk Fungsi Pangkat

Hahahaha, metode di atas memang kurang efektif untuk mencari turunan pertama fungsi pangkat, jika pangkatnya lebih dari dua. Tapi, kamu nggak perlu khawatir, nih.

Ada metode lain yang bisa kamu gunakan untuk mencari turunan pertama fungsi pangkat supaya jauh lebih cepat dan mudah. Kamu bisa gunakan aturan berikut ini!

Lho, rumus itu asalnya dari mana?

Rumus di atas, asalnya dari rumus turunan yang sudah kita pelajari sebelumnya, guys. Jadi, kalo kamu ingin mencari turunan fungsi f(x) = xⁿ, dengan n merupakan pangkat yang bisa bernilai berapa aja (n R), lalu kamu gunakan rumus turunan fungsi yang awal tadi, maka akan didapat hasil rumus turunan fungsi yang baru ini.

Coba deh, kita gunakan untuk mengerjakan soal poin c, ya.

Diketahui, f(x) = x². Berarti, konstanta a = 1 dan pangkat n = 2. Sehingga,

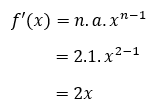
Jadi jauh lebih ringkas kan pembahasannya? Kalo gitu, bisa dong jawab pertanyaan aku yang tadi? Coba tulis jawabannya di kolom komentar, ya! Hihihihi…

Oke, guys, sekarang, gimana kalo fungsi pangkatnya itu kayak gini, f(x) = (2x – 4)⁵?

Dah, lah! Mau jadi kucing aja 🙁  (Sumber: giphy.com)

Wets! Jangan lemes dulu, bosque~~~

Kalo ada soal pangkat yang bentuknya kayak gitu, kamu bisa menyelesaikannya dengan dua cara. Cara yang pertama, jabarkan dulu persamaannya, baru cari turunannya menggunakan rumus cepat yang barusan aku spill. Tapi aku yakin, kamu pasti beneran lemes kalo pakai cara yang satu ini. HAHAHAHAHA…

Soalnya nilai pangkatnya lebih dari 2. Kalo dijabarin dulu fungsinya, jadi kurang efektif. So, aku saranin kamu pakai cara yang kedua, yaitu aturan rantai. Apa itu aturan rantai?

Aturan Rantai Turunan Fungsi Aljabar

Aturan rantai dipakai kalo fungsi yang mau kita cari turunannya itu merupakan fungsi komposisi.

Maksudnya gimana, nih?

Jadi, misalnya diketahui fungsi komposisi h(x) = f(g(x)). Untuk mencari turunan fungsi h(x) terhadap x, kita turunkan dulu fungsi luarnya (f(g(x)), kemudian kita kali dengan turunan fungsi dalamnya (g(x)).

Kaga ngarti kak jujur (Sumber: memecreator.org)

Oke, biar kamu nggak bingung, mending langsung masuk ke contoh soal aja, deh. Kita kerjakan soal di atas, ya!

Diketahui, f(x) = (2x – 4)⁵. Berarti, fungsi luarnya itu (2x – 4)⁵. Terus, fungsi dalamnya itu yang ada di dalam kurung, yaitu 2x – 4.

Pertama, kita turunkan dulu fungsi luarnya. Kita pake aturan turunan pertama fungsi pangkat, ya. Biar gampang, kita misalkan aja u = 2x – 4. Berarti f(x) = u⁵. Sehingga,

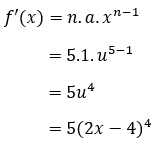
Kemudian, kita turunkan fungsi yang ada di dalam kurungnya, yaitu 2x – 4. Masih ingat kan turunan fungsi linear itu apa? Tuls! Turunannya ya koefisien variabel x-nya aja. Berarti, turunan pertama 2x – 4 adalah 2, ya.

Setelah kita tau turunan fungsi luar dan dalamnya, tinggal kita kalikan, deh. Jadi,

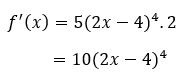
Easy, peazy, lemon strawberry, kan?

Baca Juga: Logika Matematika: Ingkaran, Konjungsi, Disjungsi, dan Biimplikasi

Rumus Turunan Fungsi Aljabar pada Operasi Perkalian dan Pembagian

Nah, dari tadi kita sudah banyak bahas cara mencari turunan fungsi pangkat, nih. Lalu, gimana ya kalo kita mau cari turunan jika fungsinya itu berupa perkalian atau pembagian?

Tenang, kamu bisa gunakan rumus berikut ini:

Seperti biasa, supaya kamu lebih mudah memahami rumus di atas, kita langsung masuk ke contoh soal.

Contoh Soal

Tentukan turunan pertama fungsi berikut:

a. f(x) = (4x³ – 3)(2x² + 1)

b.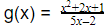

Pembahasan:

a. Kalo kamu menemukan soal kayak gini, untuk mencari turunannya, pakai aturan turunan perkalian aja, ya. Supaya lebih cepat. Jadi, nggak perlu kamu kalikan silang terlebih dahulu.

Diketahui, f(x) = (4x³ – 3)(2x² + 1). Berarti,

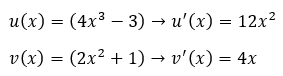
Setelah itu, tinggal kita masukkan deh ke dalam rumus.

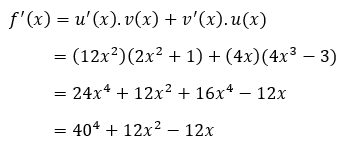
b. Diketahui, 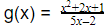. Berarti,

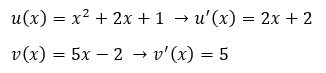
Langsung masukkan ke dalam rumusnya.

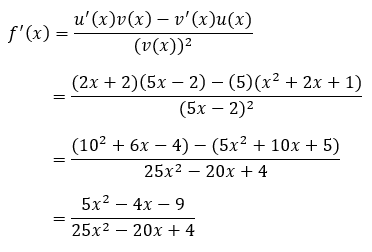
Oke, sekarang, kamu sudah paham ya tentang konsep turunan dan cara mencari turunan pertama suatu fungsi. Kita sudah cukup banyak bahas soal-soalnya juga, nih.

Nah, biar semakin manstuy lagi, ada baiknya, kamu juga harus banyak berlatih soal sendiri di rumah. Tujuannya, supaya rumus-rumus yang disampaikan di atas tadi, bisa menempel di otak tanpa harus kamu hafal.

Bagi kamu yang bingung mau cari kumpulan latihan soal di mana, kamu bisa gunakan aplikasi ruangbelajar. Semua tersedia lengkap, mulai dari level rendah, medium, hingga sulit. Ada pembahasan soalnya juga lagi. Belajar kamu jadi semakin mantep. Kurang apa lagi, yuk, kepoin sekarang!

Referensi:

Manullang, S. Kristianto, A. Hutapea, TA. dkk. (2017). Matematika SMA/MA/SMK/MAK Kelas XI. Jakarta: Kementerian Pendidikan dan Kebudayaan.

Sumber Gambar:

Gambar ‘Apa Lo Kata’ [Daring]. Tautan: https://www.memecreator.org/meme/apa-lo-kata/ (Diakses: 27 Mei 2021)

GIF ‘Seluncuran’ [Daring]. Tautan: https://giphy.com/gifs/TtznCqTy4y8py (Diakses pada: 20 Mei 2021)

GIF ‘Draco Pingsan’ [Daring]. Tautan: https://giphy.com/gifs/harry-potter-fall-gOUwm7vv70UOQ (Diakses pada: 25 Mei 2021)

Artikel ini telah diperbarui pada 5 Maret 2024.