Peluang Empiris: Konsep Dasar, Rumus dan Contoh Soal | Matematika Kelas 8

Yuk, kita bahas tentang peluang empiris, mulai dari pengertian, rumus, hingga contoh soalnya. Siapkan buku catatanmu, ya!
—
Bulan maret kemarin para pecinta bulu tangkis sempat kecewa nih, karena atlet kebanggaannya harus mundur dari All England. Padahal pertandingan itu udah dinantikan banget sama mereka. Selain karena rindu liat atletnya main di lapangan, banyak juga loh yang nggak sabar liat pertandingan Kevin/Gideon lawan Jepang (Endo/Watanabe).
Endo/Watanabe ini yang tahun lalu merebut gelar juara Kevin/Gideon guys. Sayangnya, belum sempat bertemu Endo/Watanabe mereka harus pulang. Padahal bakalan seru banget tuh kalau tahun ini mereka ketemu lagi. Banyak yang penasaran, siapa yang akan menang ya?
Nah, daripada kepikiran sampai bikin kamu nggak bisa tidur huehehe mending kita cari tau yuk peluang menang Kevin/Gideon lawan Endo/Watanabe.
Emang bisa?
Bisa dong!
Itu semua bisa dicari kalo kita paham materi peluang empiris. Jadi, apa sih Peluang empiris itu?
Pengertian dan Rumus Peluang Empiris
Peluang empiris adalah kemungkinan yang dihitung dari hasil suatu kejadian atau percobaan yang ada. Bisa juga diartikan kalo peluang empiris itu perbandingan antara banyak kejadian dengan percobaan yang dilakukan.
Baca juga: Materi Peluang: Percobaan, Ruang Sampel, dan Titik Sampel
Ohya, pengertian peluang empiris ini sama dengan frekuensi relatif suatu kejadian ya guys. Jadi, rumusnya bisa ditulis kaya gini:

Balik lagi nih sama misi awal kita untuk memprediksi kemenangan Kevin/Gideon. Jadi yang kita butuhkan adalah data rekor pertemuan mereka sebelumnya, ini dia:
Total pertandingan terakhir adalah 8 pertandingan.
Endo/Watanabe 6 kali menang.
Kevin/Gideon 2 kali menang.
Lewat data yang udah diperoleh, bisa dicari peluang empiris masing-masing kejadian.
- Peluang empiris Endo/Watanabe menang kita simbolkan dengan P(E), jadi
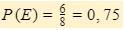
- Peluang empiris Kevin/Gideon menang bisa disimbolkan dengan P(K), jadi
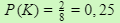
Hasilnya keliatan ya bahwa peluang empiris Kevin/Gideon menang hanya 0,5 lebih kecil dari lawannya.
Satu sifat dari peluang empiris yang harus kamu tau adalah, peluang empiris suatu kejadian selalu berada di antara 0 sampai 1. Mau apapun contoh soalnya sifat ini selalu berlaku ya. Kok bisa sih? nah supaya gampang kita ambil contoh yang tadi ya. Hasil perhitungan masing-masing peluang empiris di atas kan 0,75 dan 0,25, kedua bilangan ini ada diantara 0 dan 1. Tidak mungkin lebih dari satu atau kurang dari nol, harus dipahami nih hasil peluang empiris itu selalu bernilai positif. Logikanya, peluang Kevin/Gideon menang lawan Jepang kan nggak mungkin negatif 0,25. Atau Endo/Watanabe menang 9 kali dari 8 kali pertandingan. Makanya guys, kalau hasil perhitungan masing-masing peluang empiris mu kurang dari 0 atau lebih dari 1 pasti ada yang salah tuh sama perhitungannya, coba dicek lagi ya!
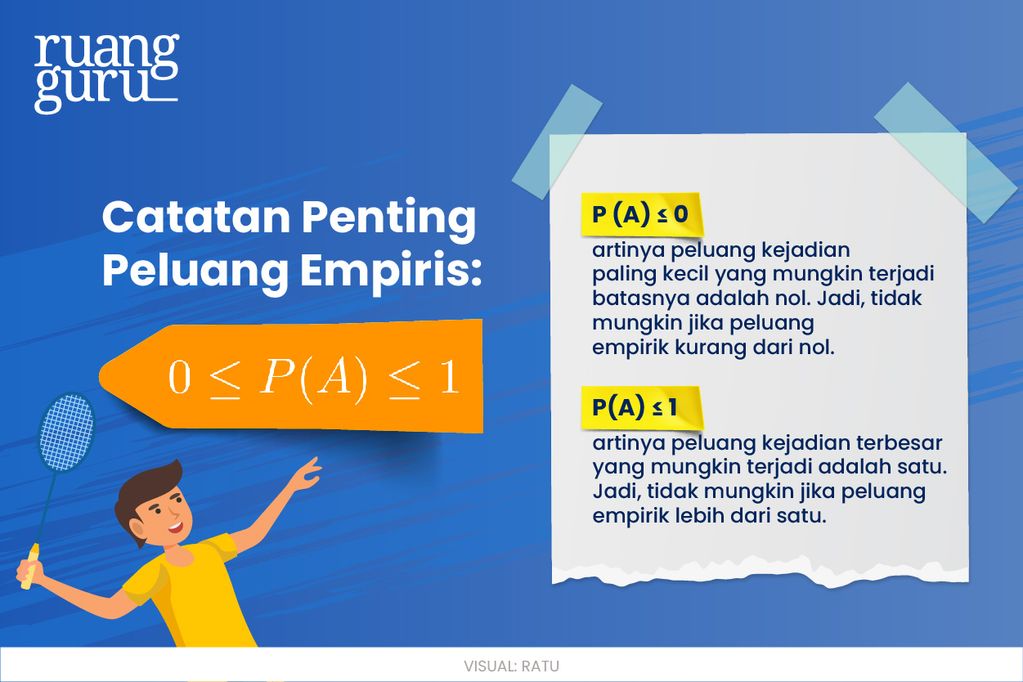
Dari pengertian, rumus dan catatan penting yang udah dibahas, mulai sekarang jangan ada yang salah konsep tentang peluang empiris ini ya. Nah, nggak asik kan abis bahas konsep tapi nggak bahas soal. Yaudah kita bahas-bahas soal yuk!
Contoh Soal Peluang Empiris
Soal 1
Tentukan peluang empiris dari suatu kejadian A, di mana muncul mata dadu 5 dari percobaan melempar sebuah dadu sebanyak 30 kali. Hasil pelemparan dadu tersebut adalah sebagai berikut:
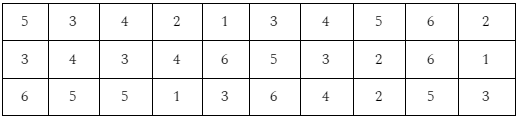
Pembahasan:
Dari soal diketahui:
Banyak kejadian muncul mata dadu 5 adalah 6 kali atau f(A) = 6
Banyak percobaan yang dilakukan atau n adalah 30 kali.
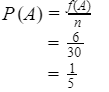
Jadi, peluang empiris kejadian A adalah ⅕ atau 0,2.
Soal 2
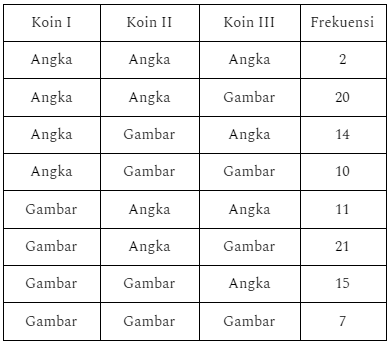
Suatu percobaan dengan tiga koin dilempar secara bersamaan. Tentukan peluang empiris munculnya 1 sisi angka dan 2 sisi gambar. Data yang diperoleh sebagai berikut:
Pembahasan:
Dari data yang diperoleh munculnya 1 sisi angka dan 2 sisi gambar adalah {(A,G,G),(G,A,G), (G,G,A)}
Frekuensi (A,G,G) adalah 10, (G,A,G) adalah 21 dan frekuensi (G,G,A) adalah 15.
Jadi, f(A) = 10 + 21 + 15 = 46
Banyaknya percobaan atau n = 100
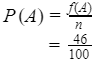
Jadi, banyaknya peluang empiris munculnya 1 sisi angka dan 2 sisi gambar dari percobaan di atas adalah 0,46.
Gimana udah lebih paham sekarang? Ohya, peluang empiris punya temen loh namanya peluang teoritis. Kedua peluang ini ada hubungannya juga, kalo dibahas jadi seru banget, penasaran? Nah, kamu bisa belajar peluang teoritis secara lengkap dan asik di ruangbelajar Soal-soal yang dikasih juga update banget plus udah dapat pembahasannya, keren kan!
Referensi:
As’ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017) Matematika SMP/MTs Kelas VIII Semester 2. Jakarta: Kementerian Pendidikan dan Kebudayaan
Sutrisno, J. dan Foster, B. (2019) Fokus Belajar Inti Sari Matematika untuk SMP/MTs. Jakarta: Penerbit Duta.
Artikel ini telah diperbarui pada 10 Juni 2022.
![[AB] Web Side Banner - Blog RG](https://cdn-web-2.ruangguru.com/landing-pages/assets/2f04a1f7-f023-4982-a02a-aee9c5891fc4.jpg)














