Cara Mencari Rumus Pola Bilangan, Jenis-Jenis & Contohnya | Matematika Kelas 8

Artikel Matematika kelas 8 ini akan membahas cara mencari rumus pola bilangan dan mengetahui perbedaan yang terdapat pada macam-macam pola bilangan, disertai contohnya.

—

Guys, coba ingat-ingat deh waktu kamu ulang tahun, kue yang diberikan orang tuamu berbentuk apa? Kalau ulang tahun teman Rogu, kue ulang tahunnya berbentuk lingkaran, nih! Yap, kebetulan kemarin adalah ulang tahun temannya Rogu. Acaranya sangat meriah sekali lho, apalagi saat pemotongan kuenya.

Ternyata saat acara pemotongan kue, Rogu tertarik pada pola pemotongan kuenya. Coba perhatikan pola potongan kue di bawah ini!

Pola potongan kue (sumber: shutterstock.com)

Sebelum kuenya dipotong, bentuk kuenya masih utuh (1 bulatan). Kemudian, setelah potongan pertama bentuk kuenya tinggal ¾. Lalu dipotong lagi menjadi ½. Nah, urutan susunan potongan kue yang teratur tersebut dinamakan pola.

Kira-kira, pola selanjutnya untuk pemotongan kue terakhir seperti apa, ya? Yuk, prediksi pola selanjutnya apa! Kamu boleh tulis jawabannya di kolom komentar di bawah, ya.

—

Tahukah kamu kalau pola tersebut termasuk ke dalam materi matematika? Yap, kalau dalam matematika, kita mengenalnya dengan pola bilangan atau pola bilangan matematika. Gimana tuh maksudnya?

Begini, teman-teman, kalau kamu perhatikan, ternyata pola potongan kue tersebut tersusun secara teratur dan tetap. Dari 1 bulatan kue, menjadi ¾, terus menjadi ½. Pola bilangannya berarti 1, 3/4, 1/2, … dan seterusnya.

Nah, dari bilangan ke-1, yaitu 1, ke bilangan ke-2, yaitu 3/4, adalah dikurangi 1/4. Begitupun dari bilangan ke-2, yaitu 3/4, ke bilangan ke-3, yaitu 1/2, juga dikurangi 1/4. Dari pola ini saja, kamu sudah bisa menebak pola potongan kue terakhir, ya.

Jadi, berdasarkan ilustrasi perhitungan di atas, bisa didefinisikan kalau pola bilangan adalah susunan bilangan yang membentuk pola teratur, atau suatu bilangan yang tersusun dari bilangan lain, sehingga membentuk suatu pola.

Pola bilangan matematika ini ada banyak jenisnya, kita kenalan yuk dengan jenis-jenis pola bilangan. Check it out!

1. Pola Bilangan Persegi

Dilihat dari namanya saja sudah terlihat bahwa pola ini akan membentuk susunan pola persegi. Yap, pola persegi adalah suatu pola yang tersusun dari beberapa bilangan berdasarkan rumus:

Coba kamu perhatikan gambar rumus pola bilangan persegi di atas. Di dalam bentuk persegi, terdapat lingkaran yang mempunyai jumlah yang berbeda-beda. Jumlah lingkaran ini adalah bilangan pola persegi.

Di suku pertama terdapat 1 lingkaran yang merupakan suku pertama pola persegi yaitu 1. Di suku kedua terdapat 4 lingkaran yang membentuk bangun persegi. Jumlah lingkaran ini merupakan suku-suku dari pola-pola bilangan persegi tersebut, dan jumlahnya akan bertambah mengikuti rumus pola bilangan persegi, yaitu n².

Tetapi bagaimana nih kalau kamu disuruh menentukan suku pola bilangan persegi yang ke-25? Maka dari itu, daripada kamu menghitung jumlah lingkaran yang membentuk bangun persegi, kamu bisa menggunakan rumusnya. Kamu hanya tinggal memasukkan bilangan 25 ke dalam rumus.

Jadi misalnya kamu ingin menentukan suku bilangan ke- 25, maka n² = 25² = 625. Gimana? Lebih simpel, kan?

Baca Juga: Pengertian, Sifat, dan Rumus Kubus Disertai Contoh

Jika kamu lebih suka menghafal, kamu bisa juga lho menghafal bilangan-bilangan pola persegi, yaitu 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, … . Tetapi disarankan untuk menggunakan rumus ya, karena dengan menggunakan rumus, kamu bisa menentukan suku pola bilangan yang besar seperti misalnya suku ke- 200.

—

Sampai sini, sudah mulai paham belum dengan materi pola bilangan? Kalo masih ada poin-poin yang belum kamu mengerti, mending belajar sama ahlinya, deh. Belajar bareng kakak-kakak pengajar di Ruangguru Privat Matematika misalnya. Hehehe…

Belajar nggak cuma menyenangkan, tapi kamu juga bakal diajari konsepnya sampai paham! Para pengajar di Ruangguru Privat juga sudah terstandarisasi kualitasnya, loh. Kamu juga bisa pilih nih, mau diajarkan secara langsung (offline) atau daring (online). Fleksibel, kan? Untuk info lebih lanjut, cuss klik link berikut!

2. Pola Bilangan Persegi Panjang

Untuk pola yang ini, pola bilangan akan tersusun seperti bentuk persegi panjang. Jadi, Pola persegi Panjang adalah suatu pola yang tersusun dari beberapa bilangan berdasarkan rumus:

Sama halnya seperti penjelasan yang ada di pola sebelumnya, jumlah lingkaran yang ada dalam bentuk persegi panjang merupakan suku-suku pada pola bilangan persegi panjang.

Perbedaan dengan pola sebelumnya adalah kalau pola persegi mempunyai bentuk persegi, sedangkan kalau pola persegi panjang mempunyai bentuk persegi panjang. Ingat, jangan sampai tertukar, ya!

Untuk rumus pola bilangan persegi panjangnya pun berbeda, rumusnya yaitu n(n + 1). Contohnya, jika kamu ingin menentukan suku ke-5 pola bilangan persegi panjang kamu hanya tinggal memasukkan ke dalam rumusnya yaitu n(n + 1) = 5(5 + 1) = 30. Gampang, kan! Berikut adalah contoh pola bilangan persegi panjang: 2, 6, 12, 20, 30, 42, 56, 72, 90, … .

Baca Juga: Unsur-Unsur Lingkaran, Ada Apa Saja, Ya?

3. Pola Bilangan Segitiga

Seperti halnya pola-pola di atas, pola bilangan segitiga juga akan membentuk susunan pola seperti segitiga. Pola bilangan Segitiga adalah suatu pola yang tersusun dari beberapa bilangan berdasarkan rumus:

Yap, untuk pola yang ini, jumlah lingkaran yang membentuk bangun segitiga merupakan pola bilangan segitiga.

Di suku pertama terdapat 1 lingkaran yang merupakan suku pertama pola bilangan segitiga. Di suku kedua terdapat 3 lingkaran yang merupakan suku kedua dari pola bilangan segitiga, dan begitupun seterusnya.

Kamu juga bisa menggunakan rumusnya agar lebih mudah mengerjakannya. Sudah paham, kan?

Berikut merupakan contoh pola bilangan segitiga: 1, 3, 6, 10, 15, 21, 28, 36, 45, … .

4. Pola Bilangan Pascal

Apa itu bilangan pascal? Sebenarnya bilangan ini ditemukan oleh seorang penemu Prancis yang bernama Blaise Pascal. Oleh karena itu, namanya jadi bilangan pascal karena diambil dari namanya, yaitu Pascal.

Bilangan ini terbentuk dari sebuah aturan geometri yang berisi susunan koefisien binomial yang bentuknya menyerupai segitiga. Di dalam segitiga pascal, penjumlahan sepasang bilangan pada satu baris yang sama menghasilkan bilangan pada baris berikutnya.

Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear Dua Variabel

Itulah tadi sekilas penjelasan mengenai bilangan pascal itu sendiri, ya. Sekarang kita bahas pola bilangan pascalnya. Jadi, pola bilangan pascal adalah suatu pola yang tersusun dari beberapa bilangan berdasarkan rumus:

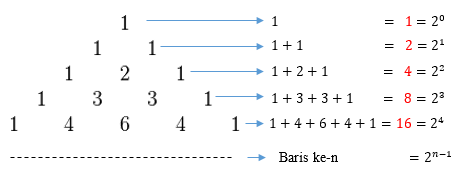
Segitiga Pascal (sumber: MathLibraryRukmantara.com)

Berdasar gambar di atas, pola bilangan pascal adalah jumlah seluruh bilangan yang ada pada baris yang sama.

Coba lihat baris terakhir (baris ke-5) pada segitiga pascal di atas. Setelah dijumlahkan hasilnya 16. Bilangan 16 inilah yang merupakan suku bilangan ke-5 (karena terdapat pada baris ke-5) dari pola bilangan pascal.

Atau kamu juga dapat langsung menggunakan rumusnya, yaitu 2^n-1. Misalnya kamu ingin mencari suku ke 10, kamu bisa langsung masukkan ke dalam rumusnya saja. Jadi, 2^10-1 = 2⁹ = 512. Berikut contoh pola bilangan pascal: 1, 2, 4, 8, 16, 32, 64, … . Seperti itu ya penjelasannya.

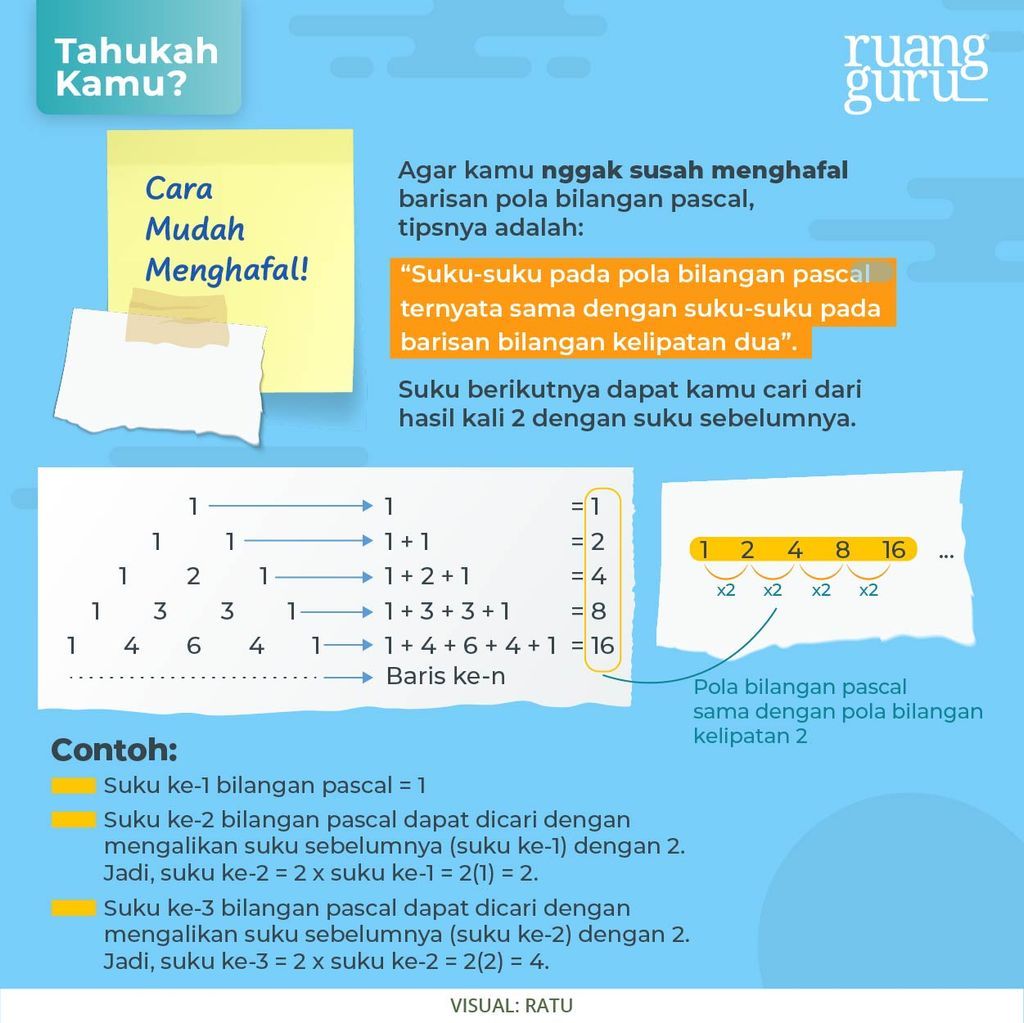
Bagaimana, sudah paham kan dengan jenis-jenis pola bilangan dan rumus untuk menentukannya? Oke lanjut yaa. Kalau tadi kita belajar pola bilangan yang sudah diketahui pasti bentuk polanya, lalu bagaimana ya cara menentukan barisan yang memiliki pola diluar pola-pola di atas tadi? Yuk, kita bahas!

Cara Menentukan Pola Bilangan dan Suku Bilangan jika Belum Diketahui Bentuk Polanya

Pada contoh soal pola bilangan di atas, kamu diperintahkan untuk menentukan suku ke-5 dan ke-6. Jadi, langkah pertama, kamu harus melihat dulu pola dari bilangan-bilangan sebelumnya.

Coba kamu lihat selisih dari tiap bilangannya. Selisih dari bilangan pertama ke bilangan kedua adalah 5. Selanjutnya selisih dari bilangan kedua ke bilangan ketiga adalah 6, dan begitu seterusnya. Ternyata selisihnya selalu bertambah satu, nih!

Langkah kedua yaitu kamu harus melakukan operasi yang sama dengan pola yang tadi telah ditemukan. Nah, untuk menentukan bilangan suku ke-5, kamu harus menambahkan bilangan ke-4 dengan 8, sehingga bilangan ke-5 adalah 23 + 8 = 31.

Sedangkan, untuk menentukan suku ke-6, kamu harus menambahkan suku ke-5 dengan 9 yah. Jadi, bilangan suku ke-6 nya adalah 31 + 9 = 40. Mantap! Kamu pasti bisa.

—

Wah ilmu kamu bertambah, deh! Sebenarnya, macam-macam pola bilangan masih banyak lagi lho, seperti pola bilangan Fibonacci, pola bilangan pangkat tiga, pola bilangan aritmatika, pola bilangan geometri, dan lain-lain.

Contoh pola bilangan dalam kehidupan sehari-hari pun banyak kita temukan. Tidak hanya pada kasus pemotongan kue di atas, ya. Ada juga pembelahan sel, amoeba yang sedang berkembang biak, susunan biji bunga daisy, susunan bola billiard, susunan biji bunga matahari, dan masih banyak lagi.

Kalau kamu mau tau lagi tentang macam-macam pola bilangan lainnya, kamu bisa nih belajar melalui video animasi di ruangbelajar. Di sana kamu bisa belajar sekaligus latihan soal-soal. Selain itu, waktu belajar kamu akan lebih efektif, dan tidak akan menyita waktu bermain kamu. Jadiii tunggu apa lagi? Buruan download aplikasi ruangguru!

Referensi:

As’ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017) Matematika SMP/MTs Kelas VIII Semester 1. Jakarta: Kementerian Pendidikan dan Kebudayaan

Sumber foto:

Ilustrasi ‘Pola Potongan Kue’ [Daring]. Tautan: https://www.shutterstock.com/da/image-vector/colorful-illustration-using-cakes-demonstrate-concept-566612620 (Diakses: 23 Desember 2020)

Ilustrasi ‘Segitiga Pascal’ [Daring]. Tautan: http://rukmannewblogaddress.blogspot.com/2017/03/manfaat-segitiga-pascal.html (Diakses: 23 Desember 2020)