Latihan Soal UNBK SMA Matematika IPS Tahun 2020

Artikel ini menyediakan beberapa soal latihan Matematika IPS SMA sebagai bahan persiapanmu untuk menghadapi Ujian Nasional (UN).

—

Topik: Relasi dan Fungsi

Subtopik: Relasi

Level Kognitif: LOTS

 

1. Jika diketahui himpunan P = {2, 3, 4, 5, 6}, dengan relasi dari P ke Q adalah “½ kalinya dari”. Maka di bawah ini yang termasuk anggota himpunan Q adalah …

A. {1, 3/2, 2, 5/2, 3}

B. {1, 2, 3, 4, 5}

C. {2, 3, 4, 5, 6}

D. {4, 6, 8, 10, 12}

E. {-2, -3, -4, -5, -6}

 

Jawaban: D

Pembahasan:

Diketahui P = {2, 3, 4, 5, 6}. Berikut masing-masing anggota P dengan relasi ½ kalinya dari.

2 sama dengan ½ kalinya dari 4.

3 sama dengan ½ kalinya dari 6.

4 sama dengan ½ kalinya dari 8.

5 sama dengan ½ kalinya dari 10.

6 sama dengan ½ kalinya dari 12.

Jadi, yang termasuk anggota himpunan Q adalah {4, 6, 8, 10, 12}.

Topik: Fungsi Komposisi

Subtopik: Invers Fungsi

Level Kognitif: MOTS

 

2. Diketahui f(x) = 6x – 8, jika f^-1(a) = 4, maka nilai 4a – 11 adalah …

A. 6

B. 11

C. 13

D. 18

E. 24

 

Jawaban: C

Pembahasan:

Perhatikan bahwa:

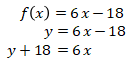
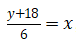, maka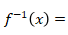

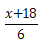
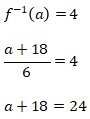, a = 6.

Maka, 4a – 11 = 4(6) – 11 = 24 – 11 = 13.

Topik: Fungsi Linear

Subtopik: Fungsi Linear

Level Kognitif: LOTS

 

3. Di antara fungsi di bawah ini, yang merupakan fungsi linear adalah …

 

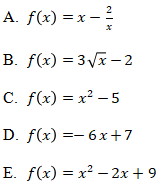
Jawaban: D

Pembahasan:

Bentuk umum fungsi linear adalah f(x) = ax + b dengan a, b ∈ R. Perhatikan bahwa f(x) = x² – 5 dan f(x) = x² – 2x + 9 adalah fungsi kuadrat serta 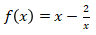dan 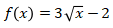memiliki x yang tidak berpangkat satu. Jadi, yang merupakan fungsi linear adalah f(x) = -6x + 7.

Topik: Fungsi Kuadrat II

Subtopik: Pertidaksamaan Kuadrat

Level Kognitif: MOTS

 

4. Nilai x yang memenuhi agar -x² + 4x + 5 ≤ 0 adalah …

A. x ≥ -5

B. x ≥ -1

C. x ≥ 5

D. x ≥ 0

E. x ≥ 2

 

Jawaban: C

Pembahasan:

Perhatikan bentuk pertidaksamaan pada soal.

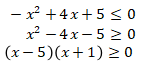
Didapat pembuat nol, yaitu x = 5 atau x = -1. Dengan menggunakan garis bilangan didapat:

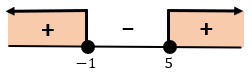
Sehingga, himpunan penyelesaian dari -x² + 4x + 5 ≤ 0 adalah {x|x ≤ -1 atau x ≥ 5, x ∈ R}. Namun, karena permintaan pada soal adalah “yang memenuhi”, maka jawaban yang tepat adalah yang termasuk ke dalam himpunan penyelesaian {x|x ≤ -1 atau x ≥ 5, x ∈ R}, yaitu terdapat pada pilihan jawaban C.

Topik: Fungsi Rasional

Subtopik: Pertidaksamaan Rasional

Level Kognitif: MOTS

 

5. Jika penyelesaian dari pertidaksamaan adalah q < x < p, maka 3p – 2q adalah …

A. -4

B. 4

C. 11

D. 15

E. 19

 

Jawaban: C

Pembahasan:

Perhatikan bahwa:

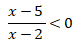
Sehingga, didapat pembuat nol dari pembilang pada bentuk rasionalnya, yaitu x = 5, dan dari penyebutnya, yaitu x = 2. Dengan menggunakan garis bilangan didapat:

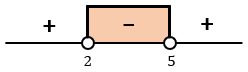
Sehingga, didapat penyelesaian 2 < x < 5.

Karena pada soal diketahui penyelesaian dari pertidaksamaan tersebut adalah q < x < p, maka p = 5 dan q = 2, sehingga 3p – 2q = 3(5) – 2(2) = 15 – 4 = 11.

Topik: Fungsi Trigonometri dan Grafiknya

Subtopik: Aturan Sinus

Level Kognitif: MOTS

 

6. Perhatikan segi-8 beraturan berikut ini:

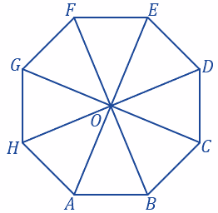
Jika panjang OD adalah 8 cm, maka luas segi-8 beraturan tersebut adalah … cm².

A. 16

B. 64

C. 64

D. 128

E. 128

 

Jawaban: E

Pembahasan:

Perhatikan bahwa segi-8 beraturan tersebut dibagi menjadi 8 buah segitiga sama kaki yang memiliki luas yang sama.

Perhatikan segitiga OAB. Karena OD = 8 cm, maka OA = OB = 8 cm.

Perhatikan bahwa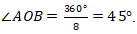

Berdasarkan aturan sinus untuk luas segitiga, maka luas segitiga OAB adalah

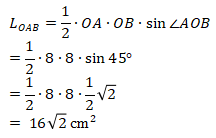
Karena segi-8 beraturan tersebut dibagi menjadi 8 buah segitiga sama kaki yang memiliki luas yang sama, maka:

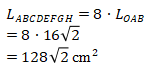
Topik: Sistem Persamaan Linear

Subtopik: Penerapan SPLDV

Level Kognitif: MOTS

 

7. Jika pembilang dan penyebut suatu pecahan masing-masing dikurangi dengan 3, maka pecahan itu menjadi ⅔. Tetapi, jika kedua-duanya ditambah 3, maka pecahan itu menjadi ⅚. Pecahan tersebut adalah …

A. 2/9

B. 5/9

C. 5/6

D. 2/3

E. 7/9

 

Jawaban: E

Pembahasan:

Misalkan: Pembilang = x, penyebut = y.

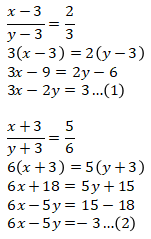
Eliminasi kedua persamaan:

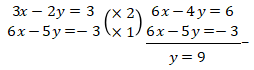
Substitusikan ke persamaan pertama:

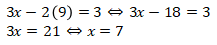
Maka, pecahan tersebut adalah x/y = 7/9.

Topik: Sistem Persamaan dan Pertidaksamaan Linear Kuadrat Dua Variabel

Subtopik: Sistem Persamaan Linear Kuadrat Dua Variabel (SPLKDV)

Level Kognitif: HOTS

 

8. Diketahui garis k melewati titik (2,4) dan menyinggung parabola y = x² – 2x + 4. Persamaan garis k adalah …

A. y = 2x + 4

B. y = -2x

C. y = 2x – 4

D. y = -2x + 4

E. y = 2x

 

Jawaban: E

Pembahasan:

Misalkan persamaan garis k adalah y = mx + c dengan m adalah gradien garis tersebut. Diketahui garis k melewati titik (2,4), maka kita mempunyai

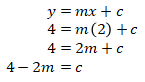
Selanjutnya, kita substitusikan c = 4 – 2m ke y = mx + c, sehingga

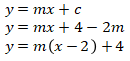
Kemudian, substitusikan y = m(x-2) + 4 ke y = x² – 2x + 4, maka kita peroleh

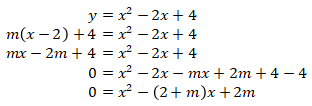
Karena garis k melewati titik (2,4) dan menyinggung parabola y = x² – 2x + 4, maka nilai diskriminan pada persamaan 0 = x² – (2 + m)x + 2m adalah nol, sehingga kita peroleh

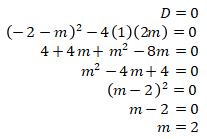
Maka, persamaan garis k adalah

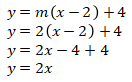
Topik: Program Linear

Subtopik: Pemodelan Matematika

Level Kognitif: LOTS

 

9. Seorang pengusaha material hendak mengangkut 110 ton barang dari gudang A ke gudang B. Untuk keperluan itu, sekurang-kurangnya diperlukan 50 kendaraan truk yang terdiri dari jenis I dengan kapasitas 3 ton dan jenis II dengan kapasitas 2 ton. Model matematika dari persamaan tersebut adalah …

 

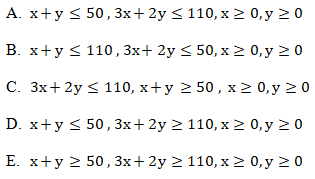
Jawaban: C

Pembahasan:

Misalkan: Truk jenis I = x, truk jenis II = y.

• “Hendak mengangkut” maka tanda yang digunakan adalah ≤ dan “sekurang-kurangnya” maka tanda yang digunakan adalah ≥.
• Penulisan model matematika jumlah truk yang digunakan:
  
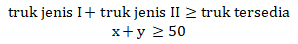
• Penulisan model matematika untuk material yang hendak diambil:

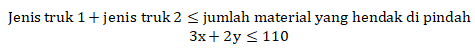
Maka, model matematika dari permasalahan tersebut adalah:

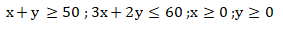
Topik: Matriks

Subtopik: Operasi Hitung Matriks I

Level Kognitif: LOTS

 

10. Jika, 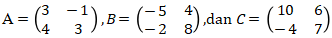, nilai A + B – C = …

 

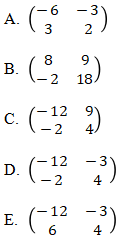
Jawaban: E

Pembahasan:

Perhatikan bahwa

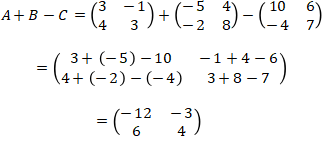
Topik: Matriks

Subtopik: Determinan Matriks

Level Kognitif: HOTS

 

11. Diketahui 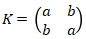dengan |a| ≠ |b| dan 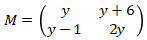dengan y adalah suatu bilangan bulat genap. Jika KM adalah matriks singular, maka y …

A. -5

B. -3

C. -2

D. 2

E. 6

 

Jawaban: D

Pembahasan:

Karena KM adalah matriks singular, maka det (KM) = 0.

Perhatikan bahwa det (KM) = det (K) . det (M), maka

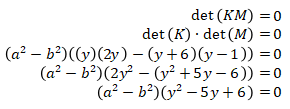
Karena |a| ≠ |b|, maka a² ≠ b², sehingga a² – b² ≠ 0. Akibatnya,

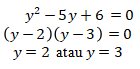
Karena y adalah suatu bilangan bulat genap, maka y = 2.

Topik: Barisan dan Deret

Subtopik: Aplikasi Deret Aritmatika

Level Kognitif: MOTS

 

12. Diketahui lima orang bersaudara dengan selisih umur yang sama. Anak yang termuda berusia 13 tahun dan yang tertua 33 tahun. Jumlah usia mereka seluruhnya adalah …

A. 112 tahun.

B. 115 tahun.

C. 125 tahun.

D. 130 tahun.

E. 160 tahun.

 

Jawaban: B

Pembahasan:

Diketahui: a = 13, n = 5, U₅ = 33.

Hitunglah nilai beda (b):

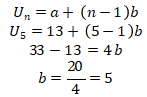
Hitunglah jumlah usia ke-5 anak tersebut:

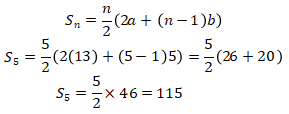
Topik: Limit I

Subtopik: Limit Aljabar

Level Kognitif: LOTS

 

13.

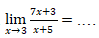
A. 0

B. 2

C. 3

D. 6

E. ∞

 

Jawaban: C

Pembahasan:

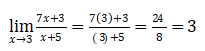
Topik: Turunan

Subtopik: Turunan Fungsi Aljabar

Level Kognitif: LOTS

 

14. Turunan pertama dari fungsi 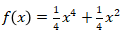adalah …

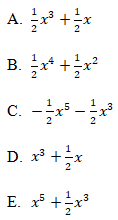
Jawaban: D

Pembahasan:

Perhatikan bahwa:

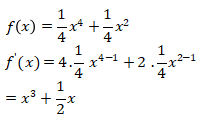
Topik: Integral

Subtopik: Teorema Dasar Kalkulus

Level Kognitif: HOTS

 

15. Dengan menggunakan jumlah Riemann dengan tak hingga persegi panjang, hasil dari 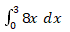adalah …

A. 34

B. 35

C. 36

D. 37

E. 38

 

Jawaban: C

Pembahasan:

Karena batas kiri = 0 dan batas kanan = 3, maka:

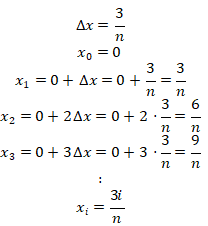
Kemudian kita cari nilai x:

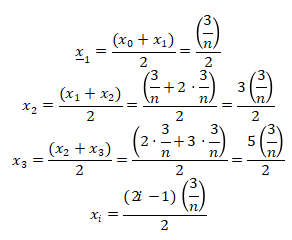
Sehingga didapat

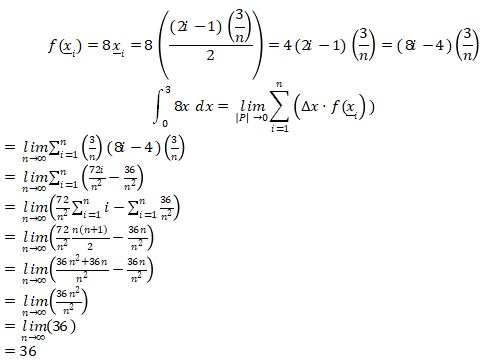
Topik: Bidang Ruang: Jarak

Subtopik: Jarak Dua Bidang Sejajar

Level Kognitif: MOTS

 

16. Pada kubus ABCD.EFGH memiliki panjang rusuk 6 cm. Jarak bidang ACF ke bidang DEG adalah … cm.

 

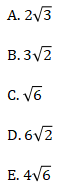
Jawaban: A

Pembahasan:

Perhatikan gambar-gambar di bawah ini.

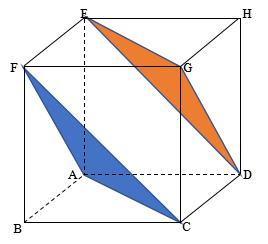
Kemudian, perhatikan bidang diagonal BDHF pada kubus ABCD.EFGH di atas.

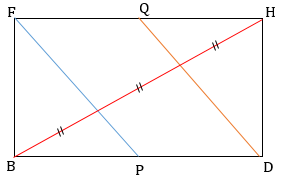
Jarak bidang ACF ke bidang CEG sama dengan jarak garis FP ke garis DQ. Jarak garis FP ke garis DQ = ⅓ HB = ⅓ (6 ) = 2

Topik: Statistika Deskriptif

Subtopik: Penyajian Data

Level Kognitif: LOTS

 

17. Perhatikan histogram di bawah ini:

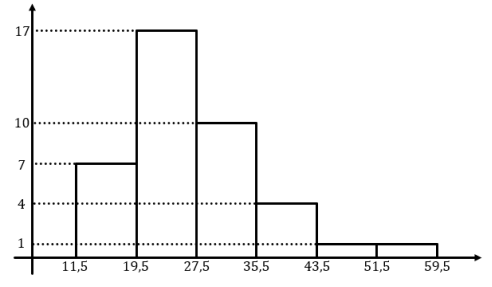
Median untuk data di atas adalah …

 

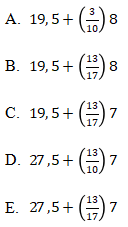
Jawaban: B

Pembahasan:

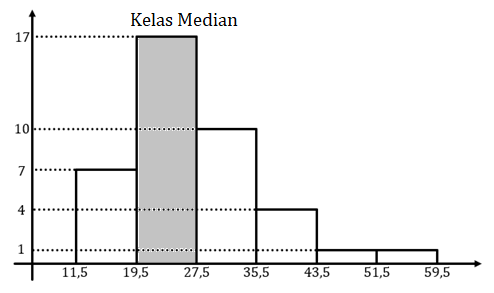
Data histogram di atas diperoleh:

Batas bawah kelas median = 19,5.

Frekuensi kumulatif sebelum kelas median (fkum) = 7.

Frekuensi kelas median (fmed) = 17.

Panjang kelas (p) = 8.

Maka,

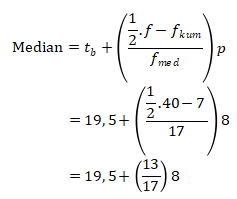
Topik: Statistika Deskriptif

Subtopik: Ukuran Pemusatan Data Tunggal

Level Kognitif: MOTS

 

18. Nilai rata-rata ujian matematika dalam suatu kelas adalah 65. Jika ditambah nilai seorang siswa baru yang nilainya 87 rata-ratanya menjadi 66. Jumlah siswa dalam kelas tersebut setelah penambahan siswa adalah …

A. 19

B. 20

C. 21

D. 22

E. 23

 

Jawaban: D

Pembahasan:

Digunakan rumus rata-rata gabungan:

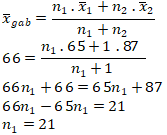
Jadi, jumlah siswa total = 21 + 1 = 22.

Topik: Statistika Deskriptif

Subtopik: Ukuran Penyebaran Data Kelompok

Level Kognitif: HOTS

 

19. Lima buah bilangan bulat positif dengan rata-rata 7, median = modus = 9. Simpangan baku yang mungkin adalah …

A. 4,8

B. 5,0

C. 6,5

D. 7,0

E. 7,2

 

Jawaban: A

Pembahasan:

Misalkan, data tersebut adalah x₁, x₂, x₃, x₄, dan x₅.

Karena modus = median = 9, maka ada dua atau lebih angka 9.

Kemungkinan I: Jika x₂ = x₃ = 9, maka x₁ < 9 dan x₄, x₅ > 9.

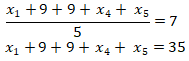
Jika dipilih bilangan terkecil positif x₁ = 1, maka x₄ + x₅ tidak mungkin hanya 16. Jadi, kemungkinan I salah.

Kemungkinan II: Jika x₃ = x₄ = 9, maka x₁, x₂ < 9 dan x₅ > 9.

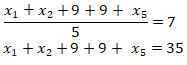
Misalkan, x₁, x₂ dipilih bilangan positif terkecil, yaitu 1, maka

x₅ = 35 – 1 – 1 – 9 – 9 = 15.

Data yang mungkin adalah 1, 1, 9, 9, 15.

Maka simpangan baku untuk data tersebut adalah

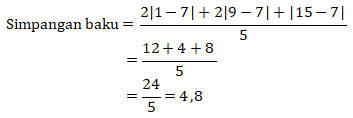
Topik: Aturan Pencacahan

Subtopik: Kombinasi

Level Kognitif: MOTS

 

20. Pada sebuah toples terdapat 7 kue nastar dan 4 sagu keju. Intan mengambil 5 kue dari toples tersebut. Banyak cara supaya kue yang diambil Intan maksimal 3 kue nastar adalah …

A. 310

B. 301

C. 294

D. 217

E. 210

 

Jawaban: B

Pembahasan:

Beberapa kasus yang terjadi dengan maksimal 3 kue nastar adalah sebagai berikut:

3 kue nastar dan 2 kue sagu keju, maka banyaknya cara adalah

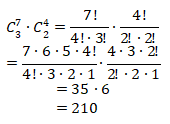
2 kue nastar dan 3 kue sagu keju, maka banyaknya cara adalah

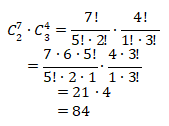
1 kue nastar dan 4 kue sagu keju, maka banyaknya cara adalah

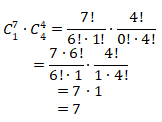
Jadi, total banyaknya cara adalah 210 + 84 + 7 = 301.

Nah, semoga soal-soal di atas tadi dapat membantumu dalam menghadapi ujian nasional nanti, ya…  Kamu juga bisa belajar materi lainnya lewat aplikasi ruangbelajar. Belajar bersama para Master Teachers handal yang bikin kamu mudah paham terhadap materi.