Contoh Soal Pengetahuan Kuantitatif TPS UTBK 2025 & Pembahasannya

Yuk, tingkatkan persiapanmu dengan contoh latihan soal TPS UTBK 2025 subtes Pengetahuan Kuantitatif beserta pembahasannya di bawah ini. Selamat mengerjakan!
—
Topik: Bilangan
Subtopik: Konsep Kilat Pola Bilangan
1. Diketahui ![]() merupakan suku ke-n dari suatu barisan geometri dengan tiga suku pertamanya berturut-turut adalah
merupakan suku ke-n dari suatu barisan geometri dengan tiga suku pertamanya berturut-turut adalah ![]() . Suku kelima dari barisan tersebut adalah ….
. Suku kelima dari barisan tersebut adalah ….

Jawaban: B
Pembahasan:
Diketahui ![]() merupakan suku ke-n dari suatu barisan geometri dengan tiga suku pertamanya berturut-turut adalah
merupakan suku ke-n dari suatu barisan geometri dengan tiga suku pertamanya berturut-turut adalah ![]() . Lalu, ditanyakan suku kelima dari barisan tersebut.
. Lalu, ditanyakan suku kelima dari barisan tersebut.
Untuk menentukan suku kelima barisan tersebut, terdapat beberapa langkah yang diperlukan seperti di bawah ini.
Langkah Pertama: Tentukan nilai dari p.
Diketahui tiga suku pertama suatu barisan geometri adalah ![]() .
.
Ingat bahwa rasio pada barisan geometri dapat ditentukan sebagai berikut.
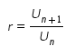
Oleh karena itu, diperoleh hubungan sebagai berikut.
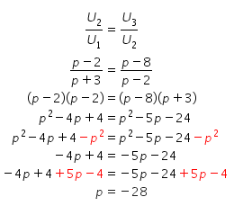
Berdasarkan perhitungan di atas, diperoleh nilai ![]() .
.
Langkah Kedua: Tentukan suku kelima barisan tersebut.
Berdasarkan nilai p yang sudah didapat, maka tiga suku pertama dari barisan tersebut adalah sebagai berikut.
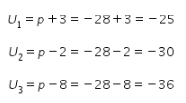
Lalu, diperoleh suku pertamanya adalah ![]() dan rasionya adalah
dan rasionya adalah ![]()
Oleh karena itu, suku kelima barisan tersebut dapat ditentukan sebagai berikut.
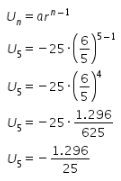
Dengan demikian, suku kelima dari barisan geometri tersebut adalah ![]() .
.
Jadi, jawaban yang tepat adalah B.

Topik: Aljabar dan Fungsi
Subtopik: Konsep Kilat Persamaan Garis Lurus
2. Diketahui persamaan garis g adalah ![]() dan persamaan garis h adalah
dan persamaan garis h adalah ![]() . Jika garis g dan garis h saling sejajar, nilai dari -2p adalah ….
. Jika garis g dan garis h saling sejajar, nilai dari -2p adalah ….
- 14
- 7
- -7
- -14
- -16
Jawaban: D
Pembahasan:
Ingat bahwa gradien dari garis dengan persamaan ![]() adalah
adalah ![]() .
.
Diketahui persamaan garis g ada ![]() .
.
Perhatikan persamaan berikut!
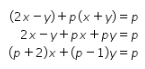
Dari bentuk tersebut, didapat bahwa gradien garis g adalah ![]() .
.
Kemudian, diketahui persamaan garis h adalah ![]() .
.
Perhatikan persamaan berikut!
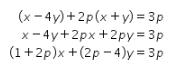
Dari bentuk tersebut, didapat bahwa gradien garis h adalah ![]() .
.
Karena garis g dan h saling sejajar, maka diperoleh hubungan sebagai berikut.
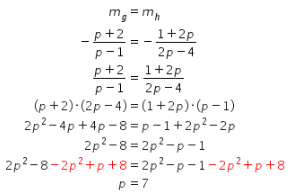
Berdasarkan perhitungan di atas, diperoleh p = 7.
Dengan demikian, nilai dari -2p adalah (-2).7 = -14.
Jadi, jawaban yang tepat adalah D.
Baca Juga: Relasi dan Fungsi: Pengertian, Syarat & Cara Menyatakannya

Topik: Geometri
Subtopik: Konsep Kilat Bangun Datar
3. Perhatikan gambar berikut!
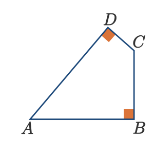
Luas dan keliling segi empat ABCD berturut-turut adalah p satuan luas dan q satuan panjang dengan p : q = 3:1 dan diketahui ![]() . Panjang
. Panjang ![]() adalah … satuan panjang.
adalah … satuan panjang.
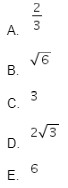
Jawaban: E
Pembahasan:
Perhatikan gambar berikut!
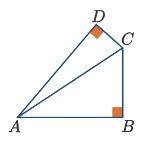
Diketahui ![]() . Misal panjang
. Misal panjang ![]() dengan a > 0, maka didapat panjang
dengan a > 0, maka didapat panjang ![]() dan
dan ![]() . Karena yang ditanyakan adalah panjang
. Karena yang ditanyakan adalah panjang ![]() , maka akan ditentukan nilai dari a.
, maka akan ditentukan nilai dari a.
Perhatikan bahwa segitiga ABC siku-siku di titik B. Oleh karena itu, berlaku Teorema Pythagoras sebagai berikut.
![]()
Kemudian, segitiga ACD siku-siku di titik D. Oleh karena itu, berlaku Teorema Pythagoras sebagai berikut.
![]()
Dengan demikian, didapat hubungan sebagai berikut.
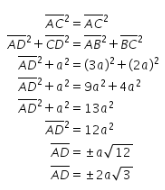
Karena panjang ![]() tidak mungkin bernilai negatif, maka panjang
tidak mungkin bernilai negatif, maka panjang ![]() .
.
Selanjutnya, luas segi empat ABCD dapat ditentukan dengan menjumlahkan luas segitiga ABC dan ACD sebagai berikut..
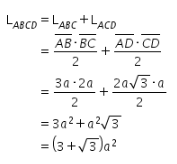
Diketahui bahwa luas segi empat ABCD adalah p satuan luas. Oleh karena itu, didapat nilai ![]() .
.
Kemudian, keliling segi empat ABCD dapat ditentukan sebagai berikut.
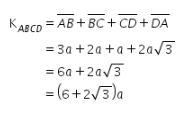
Diketahui bahwa keliling segi empat ABCD adalah q satuan panjang. Oleh karena itu, didapat nilai ![]() .
.
Karena p : q = 3 : 1, maka didapat hubungan sebagai berikut.
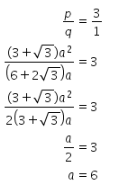
Ingat bahwa telah dimisalkan sebelumnya panjang ![]() . Dengan demikian, panjang
. Dengan demikian, panjang ![]() adalah 6 satuan panjang.
adalah 6 satuan panjang.
Jadi, jawaban yang tepat adalah E.

Topik: Statistika dan Peluang
Subtopik: Konsep Kilat Aturan Pencacahan
4. Diketahui pada suatu seleksi calon karyawan terdapat 3 orang pria dan 4 orang wanita yang duduk secara melingkar. Dalam seleksi tersebut, mereka wajib mengerjakan 8 soal dari 12 soal tes yang diberikan dan akan dipilih 3 orang yang lolos seleksi sebagai karyawan.
Berdasarkan informasi tersebut, manakah di antara pilihan berikut yang bernilai benar?
- Banyak cara duduk calon karyawan tersebut adalah 210 cara.
- Jika 5 soal pertama wajib dikerjakan, banyak kemungkinan pilihan soal yang dikerjakan dari setiap calon karyawan adalah 120 cara.
- Banyak kemungkinan variasi peserta yang lolos seleksi adalah 70.
- Banyak kemungkinan jika seorang pria dan 2 orang wanita yang lolos seleksi adalah 18.
- 1, 2, dan 3 SAJA yang benar
- 1 dan 3 SAJA yang benar
- 2 dan 4 SAJA yang benar
- HANYA 4 yang benar
- SEMUA pilihan benar
Jawaban: D
Pembahasan:
Akan ditentukan nilai kebenaran dari setiap pilihan berikut.
Pilihan 1: Banyak cara duduk calon karyawan tersebut adalah 210 cara.
Diketahui terdapat 3 orang pria dan 4 orang wanita yang duduk secara melingkar.
Ingat bahwa jika terdapat n objek yang disusun secara melingkar, maka banyak cara menyusun objek dapat dihitung dengan permutasi siklis berikut.
![]()
Pada tes seleksi calon karyawan terdapat 7 orang yang duduk melingkar. Banyak cara duduk 7 orang tersebut ditentukan sebagai berikut.
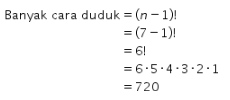
Didapat banyak cara duduk calon karyawan tersebut adalah 720 cara. Oleh karena itu, pilihan 1 bernilai SALAH.
Pilihan 2: Jika 5 soal pertama wajib dikerjakan, maka banyak kemungkinan pilihan soal yang dikerjakan dari setiap calon karyawan adalah 120 cara.
Diketahui setiap calon karyawan wajib mengerjakan 8 dari 12 soal tes yang diberikan. Jika 5 soal pertama wajib dikerjakan, maka tersisa 8 – 5 = 3 soal lagi yang harus dikerjakan dari 12 – 5 = 7 soal yang tersisa.
Banyak kemungkinan pilihan soal yang dikerjakan dari setiap karyawan dapat dihitung dengan menentukan banyak kombinasi 3 dari 7 soal yang dikerjakan, yaitu sebagai berikut.
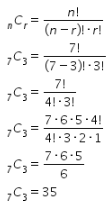
Didapat bahwa banyaknya kemungkinan pilihan soal yang dikerjakan dari setiap calon karyawan adalah 35 cara. Oleh karena itu, pilihan 2 bernilai SALAH.
Pilihan 3: Banyak kemungkinan variasi peserta yang lolos seleksi adalah 70.
Diketahui terdapat 3 orang pria dan 4 orang wanita sehingga banyak calon karyawan adalah 7 orang. Banyak kemungkinan bagi 3 orang lolos seleksi dari 7 orang tersebut dapat ditentukan dengan menghitung banyak kombinasi 3 dari 7 orang calon karyawan, yaitu ![]() .
.
Telah didapatkan dari perhitungan sebelumnya bahwa ![]() . Akibatnya, banyak kemungkinan 3 orang lolos seleksi adalah 35. Oleh karena itu, pilihan 3 bernilai SALAH.
. Akibatnya, banyak kemungkinan 3 orang lolos seleksi adalah 35. Oleh karena itu, pilihan 3 bernilai SALAH.
Pilihan 4: Banyak kemungkinan jika seorang pria dan 2 orang wanita yang lolos seleksi adalah 18.
Diketahui terdapat 3 orang pria yang mengikuti seleksi. Banyaknya cara 1 orang pria lolos seleksi dapat ditentukan dengan ![]() .
.
Diketahui juga terdapat 4 orang wanita yang mengikuti seleksi. Banyaknya cara 2 orang wanita lolos seleksi dapat ditentukan dengan ![]() .
.
Karena kejadian terpilih 1 dari 3 orang pria dan 2 dari 4 orang wanita merupakan dua kejadian yang saling bebas, maka banyak kemungkinan 1 orang pria dan 2 orang wanita lolos seleksi dapat ditentukan sebagai berikut.
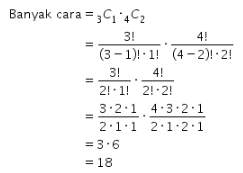
Didapat banyak kemungkinannya adalah 18. Oleh karena itu, pilihan 4 bernilai BENAR.
Dengan demikian, didapat bahwa HANYA 4 yang benar.
Jadi, jawaban yang tepat adalah D.
Baca Juga: Latihan Soal UTBK 2025 Pengetahuan dan Pemahaman Umum

Topik: Aljabar dan Fungsi
Subtopik: Konsep Kilat Fungsi
5. Diberikan sebuah fungsi ![]() dengan n merupakan suatu bilangan bulat.
dengan n merupakan suatu bilangan bulat.
Berdasarkan informasi tersebut, manakah di antara pilihan berikut yang bernilai benar?
- Jika n adalah bilangan genap,
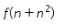 bernilai ganjil.
bernilai ganjil. - Jika n adalah bilangan ganjil,
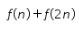 bernilai ganjil.
bernilai ganjil. 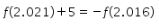
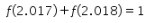
- 1, 2, dan 3 SAJA yang benar
- 1 dan 3 SAJA yang benar
- 2 dan 4 SAJA yang benar
- HANYA 4 yang benar
- SEMUA pilihan benar
Jawaban: E
Pembahasan:
Perhatikan perhitungan berikut!
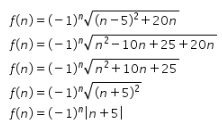
Selanjutnya, akan diperiksa tiap pernyataan yang ada.
Pilihan 1: Jika n adalah bilangan genap, ![]() bernilai ganjil.
bernilai ganjil.
Jika n bilangan genap, ![]() juga akan bernilai genap. Oleh karena itu,
juga akan bernilai genap. Oleh karena itu, ![]() juga akan bernilai genap. Artinya, untuk suatu bilangan genap
juga akan bernilai genap. Artinya, untuk suatu bilangan genap ![]() , didapat perhitungan sebagai berikut.
, didapat perhitungan sebagai berikut.
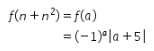
Karena a genap, maka a + 5 akan bernilai ganjil. Karena ![]() pasti merupakan bilangan ganjil, maka
pasti merupakan bilangan ganjil, maka ![]() adalah suatu bilangan ganjil.
adalah suatu bilangan ganjil.
Dengan demikian, pilihan 1 bernilai BENAR.
Pilihan 2: Jika n adalah bilangan ganjil, ![]() bernilai ganjil.
bernilai ganjil.
Jika n adalah bilangan ganjil, n + 5 akan bernilai genap. Karena ![]() pasti merupakan bilangan ganjil, maka
pasti merupakan bilangan ganjil, maka ![]() adalah suatu bilangan genap. Dengan demikian, f(n) adalah suatu bilangan genap.
adalah suatu bilangan genap. Dengan demikian, f(n) adalah suatu bilangan genap.
Kemudian, jika n adalah bilangan ganjil, 2n adalah bilangan genap.
Akibatnya, 2n + 5 akan bernilai ganjil. Oleh karena itu, ![]() adalah suatu bilangan ganjil. Dengan demikian, f(2n) adalah suatu bilangan ganjil.
adalah suatu bilangan ganjil. Dengan demikian, f(2n) adalah suatu bilangan ganjil.
Karena f(n) adalah suatu bilangan genap dan f(2n) adalah suatu bilangan ganjil, maka diperoleh bahwa ![]() adalah bilangan ganjil.
adalah bilangan ganjil.
Dengan demikian, pilihan 2 bernilai BENAR.
Pilihan 3: ![]()
Hasil dari ![]() dapat ditentukan sebagai berikut.
dapat ditentukan sebagai berikut.
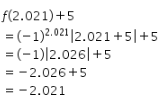
Selanjutnya, hasil dari ![]() dapat ditentukan sebagai berikut.
dapat ditentukan sebagai berikut.

Karena didapat hasil dari ![]() dan
dan ![]() yang sama, yaitu -2.021, maka
yang sama, yaitu -2.021, maka ![]() .
.
Dengan demikian, pilihan 3 bernilai BENAR.
Pilihan 4: ![]()
Hasil dari ![]() dapat ditentukan sebagai berikut.
dapat ditentukan sebagai berikut.

Karena diperoleh ![]() , maka pernyataan 4 bernilai BENAR.
, maka pernyataan 4 bernilai BENAR.
Jadi, jawaban yang tepat adalah E.

Topik: Aljabar dan Fungsi
Subtopik: Konsep Kilat Persamaan dan Fungsi Kuadrat
6. Diketahui kurva parabola ![]() ditranslasikan oleh
ditranslasikan oleh 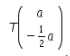 . Kemudian, bayangannya dirotasikan sejauh
. Kemudian, bayangannya dirotasikan sejauh ![]() berlawanan arah jarum jam dengan berpusat di titik asal sehingga menghasilkan bayangan akhir
berlawanan arah jarum jam dengan berpusat di titik asal sehingga menghasilkan bayangan akhir ![]() .
.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?

- Kuantitas P lebih besar daripada Q
- Kuantitas P lebih kecil daripada Q
- Kuantitas P sama dengan Q
- Tidak dapat ditentukan hubungan antara kuantitas P dan Q
Jawaban: A
Pembahasan:
Diketahui kurva parabola ![]() ditranslasikan oleh
ditranslasikan oleh 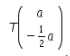 . Kemudian, bayangannya dirotasikan sejauh
. Kemudian, bayangannya dirotasikan sejauh ![]() berlawanan arah jarum jam dengan berpusat di titik asal sehingga menghasilkan bayangan akhir
berlawanan arah jarum jam dengan berpusat di titik asal sehingga menghasilkan bayangan akhir ![]() .
.
Untuk menentukan hubungan antara kuantitas P dan kuantitas Q, terdapat beberapa langkah yang diperlukan seperti di bawah ini.
Langkah Pertama: Tentukan kuantitas P.
Diketahui bahwa kuantitas P adalah jarak dua titik potong bayangan akhir dengan garis x = 3.
Untuk menentukan titik potongnya, substitusikan x = 3 ke persamaan bayangan akhir ![]() . Oleh karena itu, didapat persamaan sebagai berikut.
. Oleh karena itu, didapat persamaan sebagai berikut.
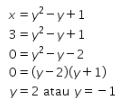
Diperoleh ordinat dari titik potongnya adalah y = 2 dan y = -1. Akibatnya, koordinat titik potong bayangan akhir dengan garis x = 3 adalah (3, 2) dan (3, -1). Karena absisnya sama, maka jarak kedua titik tersebut dapat ditentukan dengan menghitung selisih dari ordinat kedua titik sebagai berikut.
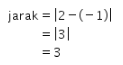
Oleh karena itu, didapat kuantitas P = 3.
Langkah Kedua: Tentukan kuantitas Q.
Diketahui bahwa kuantitas Q = a + 2.
Perhatikan bahwa kurva ![]() ditranslasikan oleh
ditranslasikan oleh 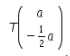 . Kemudian, bayangannya dirotasikan sejauh
. Kemudian, bayangannya dirotasikan sejauh ![]() berlawanan arah jarum jam dengan berpusat di titik asal sehingga menghasilkan bayangan akhir
berlawanan arah jarum jam dengan berpusat di titik asal sehingga menghasilkan bayangan akhir ![]() .
.
Ingat rumus translasi 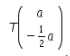 pada suatu titik berikut!
pada suatu titik berikut!
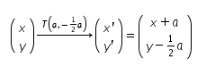
Lalu, didapat ![]() dan
dan ![]() atau dapat dituliskan dengan
atau dapat dituliskan dengan ![]() dan
dan ![]() .
.
Substitusikan bentuk x dan y yang telah didapat ke persamaan ![]() sehingga didapat persamaan sebagai berikut.
sehingga didapat persamaan sebagai berikut.
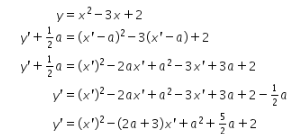
Kemudian, bayangannya dirotasikan sejauh ![]() berlawanan arah jarum jam dengan berpusat di titik asal sehingga didapat perhitungan sebagai berikut.
berlawanan arah jarum jam dengan berpusat di titik asal sehingga didapat perhitungan sebagai berikut.
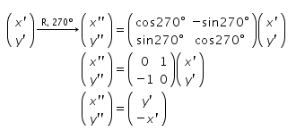
Lalu, didapat ![]() atau dapat dituliskan dengan
atau dapat dituliskan dengan ![]()
Substitusikan bentuk ![]() yang telah didapat ke persamaan
yang telah didapat ke persamaan ![]() sehingga didapat persamaan sebagai berikut.
sehingga didapat persamaan sebagai berikut.
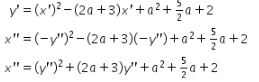
Dengan demikian, didapat bayangan akhir dari kurva tersebut adalah ![]() .
.
Telah diketahui bahwa bayangan akhirnya adalah ![]() . Oleh karena itu, didapat hubungan sebagai berikut.
. Oleh karena itu, didapat hubungan sebagai berikut.
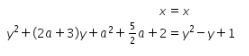
Melalui persamaan di atas, maka nilai a dapat ditentukan sebagai berikut.
1. Persamaan dari koefisien y.
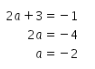
2. Persamaan dari konstanta.
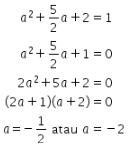
Berdasarkan dua penyelesaian tersebut, didapat nilai a yang memenuhi keduanya adalah a = -2.
Oleh karena itu, didapat kuantitas Q = a + 2 = -2 + 2 = 0.
Berdasarkan langkah pertama dan kedua, diperoleh kuantitas P = 3 dan kuantitas Q = 0 sehingga kuantitas P lebih besar daripada Q.
Dengan demikian, kuantitas P lebih besar daripada Q.
Jadi, jawaban yang tepat adalah A.

Topik: Statistika dan Peluang
Subtopik: Konsep Kilat Teori Peluang
7. Perusahaan X melakukan pengundian doorprize untuk satu orang pemenang. Diketahui peluang terpilihnya karyawan berusia 22—25 tahun adalah 0,18, karyawan berusia 26—30 tahun adalah 0,32, dan sisanya karyawan berusia 31—35 tahun. Diketahui pula peluang terpilihnya karyawan pria dalam rentang usia 31—35 tahun adalah 0,16.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?

- Kuantitas P lebih besar daripada Q.
- Kuantitas P lebih kecil daripada Q.
- Kuantitas P sama dengan Q.
- Tidak dapat ditentukan hubungan antara kuantitas P dan Q.
Jawaban: C
Pembahasan:
Diberikan permisalan sebagai berikut.
A: Kejadian terpilihnya karyawan berusia 22—25 tahun.
B: Kejadian terpilihnya karyawan berusia 26—30 tahun.
C: Kejadian terpilihnya karyawan berusia 31—35 tahun.
M: Kejadian terpilihnya karyawan pria.
Akan diperiksa kuantitas P.
Perhatikan bahwa peluang terpilihnya karyawan pria jika diketahui karyawan tersebut berusia 31—35 tahun merupakan kejadian bersyarat yang dapat ditentukan sebagai berikut.
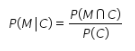
Karena karyawan di Perusahaan X memiliki kemungkinan 22—25 tahun, 26—30 tahun, atau 31—35 tahun, maka peluang terpilihnya karyawan berusia 31—35 tahun dapat ditentukan sebagai berikut.
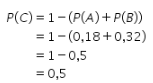
Kemudian, dari soal juga diketahui peluang terpilihnya karyawan pria dalam rentang usia 31—35 tahun adalah 0,16. Artinya, didapat ![]()
Dengan demikian, diperoleh perhitungan sebagai berikut.
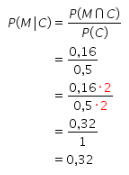
Oleh karena itu, kuantitas P adalah 0,32.
Kemudian, perhatikan bahwa kuantitas Q adalah 0,32. Artinya, kuantitas P dan Q bernilai sama.
Dengan demikian, kuantitas P sama dengan Q.
Jadi, jawaban yang tepat adalah C.
Baca Juga: Statistika Deskriptif dalam Data Berinterval, Rumus, dan Contohnya

Topik: Bilangan
Subtopik: Konsep Kilat Himpunan
8. Andre, Sansa, dan Banu memiliki sejumlah mata pelajaran favorit yang saling beririsan satu sama lain. Andre menyukai 8 mata pelajaran, Sansa menyukai 9 mata pelajaran, dan Banu menyukai 10 mata pelajaran. Banu tidak menyukai 2 mata pelajaran favorit Andre dan Sansa, tetapi Banu menyukai 3 mata pelajaran favorit Sansa. Kemudian, sebanyak 2 mata pelajaran hanya disukai oleh Andre. Jika tidak ada mata pelajaran yang sama sekali tidak disukai ketiganya, maka berapa banyak mata pelajaran favorit Banu dan Sansa yang bukan mata pelajaran favorit Andre?
Putuskan apakah pernyataan 1 dan 2 berikut cukup untuk menjawab pertanyaan tersebut.
- Banyaknya mata pelajaran favorit ketiganya adalah 1.
- Banyaknya mata pelajaran favorit Andre yang bukan mata pelajaran favorit Banu adalah 4.
- Pernyataan 1 SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan 2 SAJA tidak cukup.
- Pernyataan 2 SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan 1 SAJA tidak cukup.
- DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
- Pernyataan 1 SAJA cukup untuk menjawab pertanyaan dan pernyataan 2 SAJA cukup.
- Pernyataan 1 dan pernyataan 2 tidak cukup untuk menjawab pertanyaan.
Jawaban: A
Pembahasan:
Dimisalkan himpunan-himpunan sebagai berikut.
A: Himpunan mata pelajaran favorit Andre.
B: Himpunan mata pelajaran favorit Banu.
C: Himpunan mata pelajaran favorit Sansa.
Diketahui bahwa ![]()
Jika banyaknya mata pelajaran favorit ketiganya adalah x dan banyaknya mata pelajaran favorit dari Banu dan Sansa yang tidak disukai oleh Andre adalah y, informasi-informasi pada soal tersebut dapat diilustrasikan dalam diagram Venn berikut.
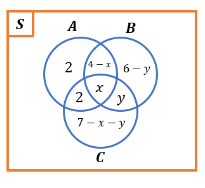
Diketahui bahwa Banu menyukai 3 mata pelajaran favorit Sansa. Artinya, didapat bahwa ![]() .
.
Selanjutnya, akan diperiksa setiap pernyataan yang diberikan.
Pernyataan 1: Banyaknya mata pelajaran favorit ketiganya adalah 1.
Berdasarkan informasi tersebut, maka didapat nilai x = 1. Akibatnya, didapat diagram Venn sebagai berikut.
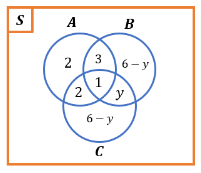
Diketahui bahwa Banu menyukai 3 mata pelajaran favorit Sansa. Akibatnya, didapat ![]()
Berdasarkan gambar tersebut, didapat bahwa ![]() . Oleh karena itu, diperoleh perhitungan sebagai berikut.
. Oleh karena itu, diperoleh perhitungan sebagai berikut.
Artinya, banyaknya mata pelajaran favorit Banu dan Sansa yang bukan mata pelajaran favorit Andre adalah 1.
Oleh karena itu, pernyataan 1 SAJA cukup untuk menjawab pertanyaan.
Pernyataan 2: Banyaknya mata pelajaran favorit Andre yang bukan mata pelajaran favorit Banu adalah 4.
Berdasarkan gambar diagram Venn di awal pembahasan, telah didapat bahwa banyaknya mata pelajaran favorit Andre yang bukan mata pelajaran favorit Banu adalah 2 + 2 = 4.
Artinya, tidak ada informasi tambahan yang dapat digunakan untuk menentukan nilai y.
Oleh karena itu, pernyataan 2 SAJA tidak cukup untuk menjawab pertanyaan.
Dengan demikian, dapat disimpulkan bahwa pernyataan 1 SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan 2 SAJA tidak cukup.
Jadi, jawaban yang tepat adalah A.
Baca Juga: Latihan Soal TPS UTBK 2025 Kemampuan Memahamai Bacaan dan Menulis

Topik: Pengetahuan Kuantitatif
Subtopik: Bilangan
9. Tentukan nilai yang tepat untuk mengisi tempat yang kosong pada gambar di bawah ini.
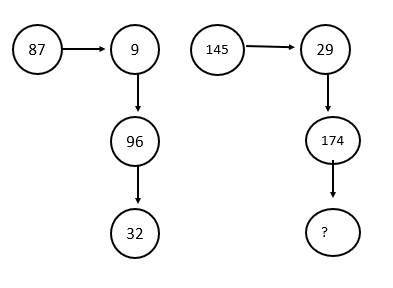
- 35
- 45
- 87
- 24
- 58
Jawaban: E
Pembahasan:
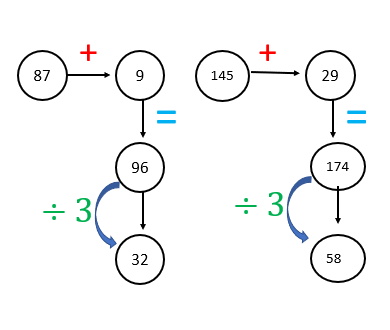

Topik: Pengetahuan Kuantitatif
Subtopik: Bilangan
10. Perhatikan gambar berikut!
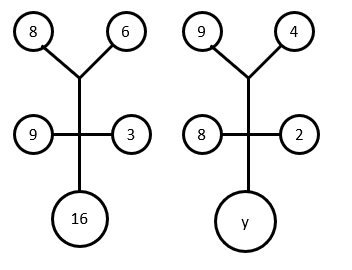
Nilai y yang memenuhi adalah …
- 9
- 14
- 18
- 20
- 36
Jawaban: A
Pembahasan:
Perhatikan penyelesaian gambar yang pertama.
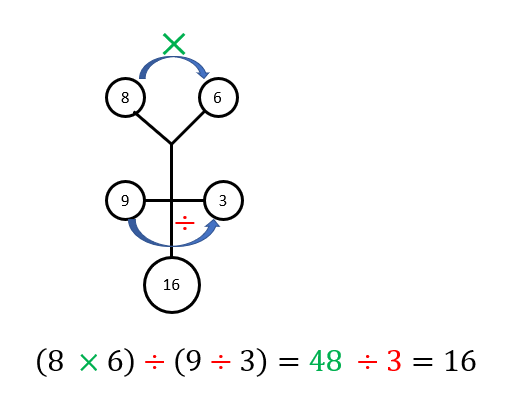
Terapkan langkah penyelesaian dari gambar pertama pada gambar kedua.
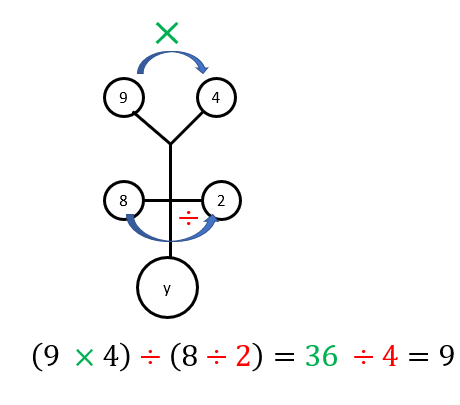

Topik: Pengetahuan Kuantitatif
Subtopik: Aljabar
11. Jika diketahui nilai m ⋅ n = 10 dan nilai m – n = 3, maka nilai m3 – n3 adalah …
- 27
- 29
- 43
- 63
- 117
Jawaban: E
Pembahasan:
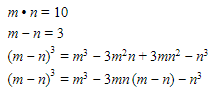
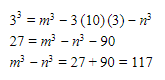

Topik: Pengetahuan Kuantitatif
Subtopik: Bilangan
12. Jika diketahui nilai a = 3 dan b = 2, maka nilai dari 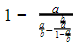 adalah …
adalah …
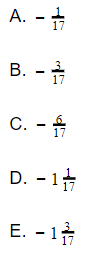
Jawaban: A
Pembahasan:
a = 3 dan b = 2
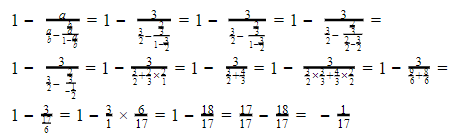

Topik: Pengetahuan Kuantitatif
Subtopik: Aljabar
13. Jika diketahui x ≠ 0 dan x ≠ 3/2, maka hasil dari perkalian 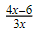 dengan
dengan 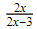 adalah …
adalah …
- 2/3
- – 2/3
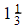
- 2
- -2
Jawaban: C
Pembahasan:
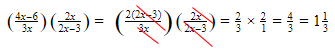

Topik: Pengetahuan Kuantitatif
Subtopik: Bilangan
14. Suatu proyek dijadwalkan akan selesai dalam waktu 30 hari jika dikerjakan oleh 60 orang pekerja. Memasuki hari ke 21, ada 20 orang pekerja yang sakit dan baru bekerja lagi 5 hari setelahnya, ada 20 orang pulang ke kampung halaman dan kembali setelah 5 hari. Jika setiap pekerja memiliki kemampuan yang sama dan agar proyek selesai tepat waktu, jumlah minimal pekerja yang harus ditambah adalah … pekerja.
- 20
- 40
- 100
- 140
- 220
Jawaban: B
Pembahasan:
Misalkan, banyak pekerja = x.
Diketahui:

Banyak pekerjaan di 5 hari terakhir adalah 500 pekerjaan.
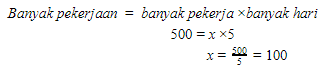
Banyak pekerja di 5 hari terakhir adalah 100 orang dan yang sudah ada adalah 60 orang.
Jadi, banyak pekerja yang harus ditambah adalah 40 orang.

Topik: Pengetahuan Kuantitatif
Subtopik: Aljabar
15. Empat tahun yang lalu rata-rata umur ayah, ibu, dan kakak adalah 34 tahun. Tiga tahun yang lalu rata-rata umur ayah dan kakak adalah 32 tahun. Manakah hubungan yang benar antara kuantitas P dan Q berikut berdasarkan informasi yang diberikan?

- P > Q
- Q > P
- P = Q
- Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.
Jawaban: B
Pembahasan:
Misalkan:
- Umur ayah = x
- Umur ibu = y
- Umur kakak = z
Rata-rata umur ayah, ibu, dan kakak 4 tahun yang lalu = 34 tahun.
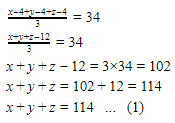
Rata-rata umur ayah dan kakak 3 tahun yang lalu = 32 tahun.
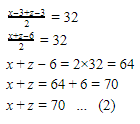
Dari persamaan (1) dan (2) didapatkan:
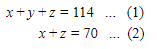
Nilai x + z = 70 substitusikan ke persamaan (1):
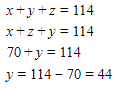
y adalah umur ibu, jadi umur ibu adalah 44 tahun.
Kemudian, lihat tabel:

P = 44 tahun
Q = 45 tahun
Nilai Q > P.
Jadi, pilihan yang tepat adalah B.

Topik: Pengetahuan Kuantitatif
Subtopik: Geometri, Aljabar
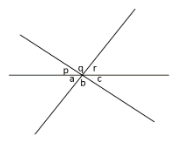
16. Tentukan nilai r?
(1) a + c = 85o
(2) b + c = 130o
- (1) saja cukup, tapi (2) saja tidak cukup.
- (2) saja cukup,tapi (1) saja tidak cukup.
- Dua pernyataan bersama-sama cukup untuk menjawab pertanyaan, tetapi satu pernyataan saja tidak cukup.
- (1) saja cukup, dan (2) saja cukup.
- (1) dan (2) tidak cukup.
Jawaban: B
Pembahasan:
Perhatikan gambar!
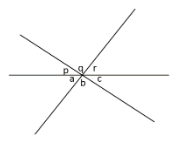
Oleh karena itu, didapat
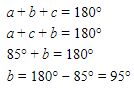
Karena besar r = a, dan nilai a belum dapat diketahui nilainya, maka pertanyaan tidak dapat dijawab hanya dengan pernyataan (1).
Pernyataan (2)
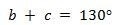
Oleh karena itu, didapat
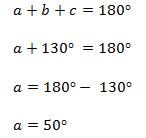
Karena besar r = a, maka didapat 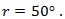
Oleh karena itu, pertanyaan dapat dijawab hanya dengan pernyataan (2).
Jadi, pernyataan (2) saja cukup untuk menjawab pertanyaan, tapi pernyataan (1) saja tidak cukup.

Topik: Pengetahuan Kuantitatif
Subtopik: Geometri
17. Suatu kebun berbentuk lingkaran, jika di sekeliling kebun akan ditanami pohon dengan jarak antar pohonnya adalah 2 meter. Berapa banyak pohon yang dibutuhkan?
Putuskan pernyataan (1) atau (2) atau keduanya yang cukup untuk menjawab pertanyaan tersebut.
(1) Luas kebun = 15.400 m2
(2) Keliling kebun = 440 m
- (1) saja cukup, tapi (2) saja tidak cukup.
- (2) saja cukup,tapi (1) saja tidak cukup.
- Dua pernyataan bersama-sama cukup untuk menjawab pertanyaan, tetapi satu pernyataan saja tidak cukup.
- (1) saja cukup, dan (2) saja cukup.
- (1) dan (2) tidak cukup.
Jawaban: D
Pembahasan:
Dari soal, diketahui kebun berbentuk lingkaran dan jarak antar pohon adalah 2 meter.
Ditanyakan: banyak pohon yang dibutuhkan untuk ditanam di sekeliling kebun.
Untuk menentukan banyak pohon yang dibutuhkan untuk ditanam, yang perlu diketahui adalah kelilingnya.
Pernyataan (1)
Luas kebun = 15.400 m2
Karena kebun berbentuk lingkaran,
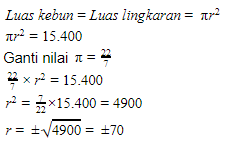
Tapi karena r adalah ukuran panjang, nilainya pasti positif. Jadi, r = 70 m.
Keliling kebun = keliling lingkaran = 2πr.
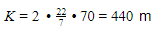
Banyak pohon yang dibutuhkan:
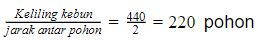
Dengan pernyataan (1) saja sudah dapat menjawab pertanyaan.
Pernyataan (2)
Keliling kebun = 440 m
Banyak pohon yang dibutuhkan:
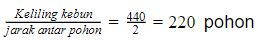
Dengan pernyataan (2) saja sudah dapat menjawab pertanyaan.
Jadi, pilihan yang tepat adalah D

Topik: Pengetahuan Kuantitatif
Subtopik: Peluang
18. Median tujuh bilangan adalah 12, 18, 6, x, 18, 4, 24 adalah x.
Manakah hubungan yang benar antara kuantitas P dan Q berikut berdasarkan informasi yang diberikan?

- P > Q
- Q > P
- P = Q
- 2P = Q
- Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.
Jawaban: B
Pembahasan:
Pertama, urutkan data dari tujuh bilangan. Karena x adalah median dari 7 bilangan, artinya x berada di tengah urutan.
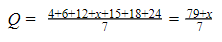
Rata-rata data jika nilai x = 13:
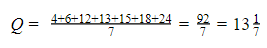
Jika x = 13, maka Q > P.
Rata-rata data jika nilai
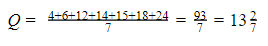
Jika x = 14, maka P > Q.
Karena tidak dapat memutuskan mana jawaban yang tepat, kesimpulannya adalah Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.

Topik: Pengetahuan Kuantitatif
Subtopik: Geometri
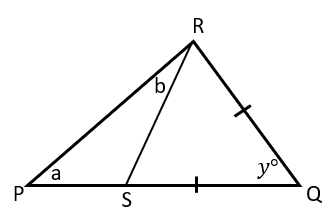
19. Segitiga QRS adalah segitiga sama kaki dengan QR = QS. Titik P terletak pada garis perpanjangan QS. Jika a = 48o dan b = 22o, maka nilai y adalah …
- 40o
- 44o
- 48o
- 60o
- 70o
Jawaban: A
Pembahasan:
Perhatikan gambar!
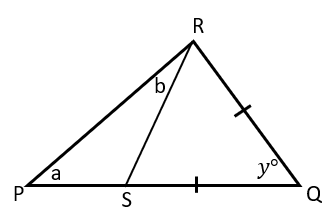
Perhatikan segitiga PRS, a = 48o , dan b = 22o .
Jumlah sudut pada segitiga adalah 180o.
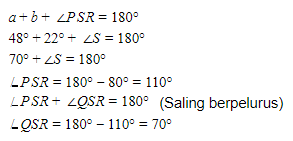
Perhatikan segitiga QRS yang merupakan segitiga sama kaki dengan QR = QS, sehingga:
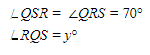
Jumlah sudut pada segitiga adalah 180o.
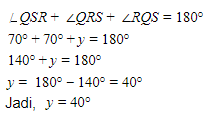

Topik: Pengetahuan Kuantitatif
Subtopik: Aljabar
20. Suatu garis pada bidang xy melalui titik (2,-1) dan mempunyai gradien 1/2. Manakah di antara titik dengan koordinat berikut yang terletak pada garis itu?
(1) (0,2)
(2) (-2,0)
(3) (2, -1/2)
(4) (4,0)
- (1),(2), dan (3) SAJA yang benar.
- (1) dan (3) SAJA yang benar.
- (2) dan (4) SAJA yang benar.
- HANYA (4) yang benar.
- SEMUA pilihan benar.
Jawaban: D
Pembahasan:
Untuk menentukan koordinat yang terletak pada garis, maka tentukan terlebih dahulu persamaan garis yang melalui titik tersebut.
Garis melalui titik (2,-1) dan mempunyai gradien m = 1/2 dapat ditentukan menggunakan persamaan:
Ganti nilai x1, y1, dan m dengan nilai yang diketahui dari soal, yaitu:
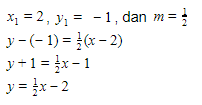
Untuk menentukan titik koordinat yang terletak pada garis dapat dilakukan dengan memasukkan koordinat yang ada pada soal ke persamaan garis yang didapat, yaitu  .
.
(1) (0,2)
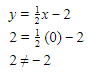
 .
.(2) (-2,0)
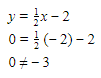
 .
.(3) (2, 1/2)
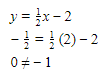
 .
.(4) (4,0)
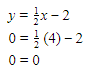
 .
.Jadi, pilihan yang tepat adalah D yaitu HANYA (4) saja yang benar.

Topik: Pengetahuan Kuantitatif
Subtopik: Peluang
21. Tersedia 8 kursi yang disusun berjajar dan setiap kursi ditempati paling banyak oleh satu orang. Manakah hubungan yang benar antara kuantitas P dan Q berdasarkan informasi berikut.

- P > Q
- Q > P
- P = Q
- 2P = Q
- Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.
Jawaban: B
Pembahasan:
Dari soal diketahui banyak kursi yang tersedia adalah 8 kursi dan hanya akan diduduki oleh 4 orang.
Banyak susunan 4 orang duduk pada kursi yang disediakan adalah P.
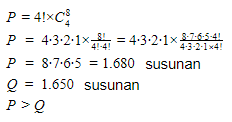
Jadi, jawaban yang tepat adalah A.

Topik: Pengetahuan Kuantitatif
Subtopik: Peluang
22. Sebuah lemari arsip memiliki p laci. Setiap laci dapat memuat 5 wadah amplop, dan setiap wadah amplop coklat dapat memuat r amplop coklat. Berapa amplop coklat yang terdapat pada 3 lemari?
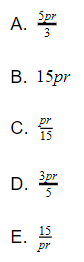
Jawaban: B
Pembahasan:
Dari soal diketahui ada 3 lemari.
Setiap lemari terdapat p laci.
Setiap laci terdapat 5 wadah amplop.
Setiap wadah amplop terdapat r amplop.
Jadi, di dalam 3 lemari terdapat:
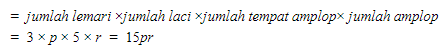
Jadi, jawaban yang tepat adalah B.

Topik: Pengetahuan Kuantitatif
Subtopik: Peluang
23. Suatu perusahaan mempekerjakan 25 karyawan. Perusahaan memberi gaji masing-masing Rp8.000.000,00 pada 8 karyawan, Rp6.000.000,00 pada 10 karyawan, dan Rp5.000.000,00 pada 7 karyawan. Rata-rata gaji 25 karyawan tersebut berkisar pada …
- Rp5.360.000,00
- Rp6.360.000,00
- Rp7.360.000,00
- Rp8.360.000,00
- Rp9.360.000,00
Jawaban: B
Pembahasan:
Dari soal diketahui:
Karyawan yang memiliki gaji Rp8.000.000,00 ada 8 orang.
Karyawan yang memiliki gaji Rp6.000.000,00 ada 10 orang.
Karyawan yang memiliki gaji Rp5.000.000,00 ada 7 orang.
Jumlah karyawan seluruhnya ada 25 orang.
Dengan menggunakan rumus rata-rata:
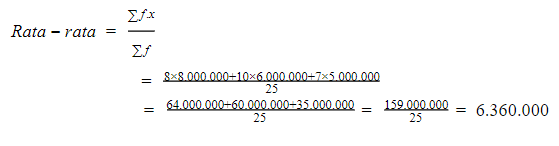
Jadi, rata-rata gaji 25 karyawan berkisar Rp6.360.000,00.

Topik: Pengetahuan Kuantitatif
Subtopik: Peluang
24. Jumlah dari suatu himpunan bilangan adalah 2.091. Berapa rata-ratanya?
1) Bilangan terbesar adalah 149 dan bilangan terkecil adalah 41.
2) Anggota himpunan bilangan adalah 17.
- (1) saja cukup, tapi (2) saja tidak cukup.
- (2) saja cukup,tapi (1) saja tidak cukup.
- Dua pernyataan bersama-sama cukup untuk menjawab pertanyaan, tetapi satu pernyataan saja tidak cukup.
- (1) saja cukup, dan (2) saja cukup.
- (1) dan (2) tidak cukup.
Jawaban: B
Pembahasan:
Untuk menentukan rata-rata dari suatu himpunan bilangan adalah dengan menjumlahkan semua data dibagi dengan banyak data.
Dari soal diketahui jumlah himpunan bilangan adalah 2.091.
Pernyataan 1 adalah Bilangan terbesar adalah 149 dan bilangan terkecil adalah 41.
Pernyataan ini tidak membantu untuk mendapatkan nilai rata-rata dari bilangan tersebut.
Pernyataan 2 adalah Anggota himpunan bilangan adalah 17.
Banyaknya anggota himpunan bilangan sama artinya dengan banyak bilangan yang terdapat dalam himpunan bilangan, sehingga dapat membantu untuk menentukan nilai rata-rata himpunan, yaitu:
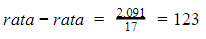
Jawaban yang tepat adalah B karena pernyataan 2 saja cukup, tetapi pernyataan 1 saja tidak cukup.

Topik: Pengetahuan Kuantitatif
Subtopik: Peluang
25. Berapa median dari himpunan K?
1) K mengandung 5 bilangan bulat.
2) Rata-rata dan modus dari K sama-sama bernilai 12.
- (1) saja cukup, tapi (2) saja tidak cukup.
- (2) saja cukup,tapi (1) saja tidak cukup.
- Dua pernyataan bersama-sama cukup untuk menjawab pertanyaan, tetapi satu pernyataan saja tidak cukup.
- (1) saja cukup, dan (2) saja cukup.
- (1) dan (2) tidak cukup.
Jawaban: E
Pembahasan:
Untuk menentukan median dari suatu himpunan bilangan adalah dengan mengurutkan semua data dari yang terkecil sampai yang terbesar.
Dari pernyataan 1), diketahui jumlah anggota himpunan K adalah 5 bilangan bulat, tetapi tidak diketahui anggota-anggota himpunannya sehingga kita tidak dapat menentukan median dari himpunan K.
Dari pernyataan 2), yang diketahui nilai rata-rata dan nilai dari modus. Data ini tidak membantu kita dalam menentukan nilai median.
Sehingga, pernyataan 1) dan pernyataan 2) tidak cukup untuk menjawab pertanyaan

Topik: Pengetahuan Kuantitatif
Subtopik: Geometri
26. Jika AB = AC, berapakah luas segitiga ABC?
1) Sudut ABC= 60°
2) BC = 10
- (1) saja cukup, tapi (2) saja tidak cukup.
- (2) saja cukup,tapi (1) saja tidak cukup.
- Dua pernyataan bersama-sama cukup untuk menjawab pertanyaan, tetapi satu pernyataan saja tidak cukup.
- (1) saja cukup, dan (2) saja cukup.
- (1) dan (2) tidak cukup.
Jawaban: C
Pembahasan:
Dari soal diketahui bahwa panjang sisi AB = AC.
Pernyataan 1) diketahui 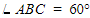 . Karena AB = AC, maka besar
. Karena AB = AC, maka besar 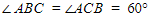 , sehingga
, sehingga 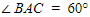 .
.
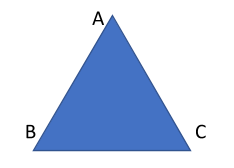
Namun, untuk menentukan luas segitiga ABC tidak dapat ditentukan jika hanya diketahui besar sudut dari segitiga. Jadi, pernyataan 1 saja tidak cukup untuk menentukan luas segitiga.
Lalu, dari pernyataan 2) diketahui bahwa panjang BC = 10 cm dan dari pernyataan 1) kita mengetahui bahwa segitiga ABC adalah segitiga sama sisi, sehingga kita dapat menentukan luas dari segitiga ABC menggunakan rumus: 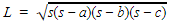 .
.
Tapi, jika hanya diketahui panjang sisi BC saja tanpa diketahui besar sudutnya, maka kita juga tidak dapat menentukan luas segitiganya.
Jadi, jawaban A SALAH karena pernyataan 1) saja tidak cukup atau pernyataan 2) saja tidak cukup.
Jawaban B SALAH karena pernyataan 2) saja tidak cukup dan pernyataan 1) saja tidak cukup.
Jawaban C BENAR karena dua pernyataan bersama-sama cukup untuk menjawab pertanyaan, tetapi satu pernyataan saja tidak cukup.
Jawaban D SALAH karena pernyataan 1) saja tidak cukup atau pernyataan 2) saja tidak cukup.
Jawaban E SALAH karena pernyataan 1) dan 2) secara bersama-sama cukup untuk menjawab pertanyaan.

Topik: Pengetahuan Kuantitatif
Subtopik: Geometri
27. Jika sebuah segitiga memiliki sisi dengan panjang 6 dan 10, manakah dari pernyataan berikut ini yang mungkin sebagai panjang sisi ketiga?
1) 4
2) 8
3) 16
- (1) saja
- (2) saja
- (1) dan (2) saja
- (1) dan (3) saja
- (1). (2) dan (3)
Jawaban: B
Pembahasan:
Tiga buah sisi dikatakan membentuk segitiga bila berlaku teorema pertidaksamaan segitiga, dimana jumlah panjang dua sisi segitiga selalu lebih panjang dari pada sisi yang ketiga.
Jadi, bila ada tiga buah panjang sisi segitiga dengan panjang a, b, dan c dikatakan membentuk segitiga bila terpenuhi ketiga syarat, yaitu:
1. a + b > c
2. a + c > b
3. b + c > a
Jika kita misalkan bahwa a = 6 cm dan b = 10 cm, maka kita dapat menentukan nilai c dengan menggunakan:
Syarat 1:
a + b > c,
6 + 10 > c
16 > c atau dapat kita tuliskan menjadi c < 16.
Syarat 2:
a + c > b atau dapat dituliskan menjadi b – a < c.
10 – 6 < c
4 < c atau dapat dituliskan menjadi c > 4.
Syarat 3:
b + c > a atau dapat kita tuliskan menjadi a – b < c.
6 – 10 < c

Topik: Pengetahuan Kuantitatif
Subtopik: Aljabar
28. Jika x2 + bx + 24 = 9, berapa b?
1) (x + 5) merupakan salah satu faktor dari x2 + bx + 26 = 8.
2) -3 merupakan salah satu akar dari x2 + bx + 26 = 8.
- (1) saja cukup, tapi (2) saja tidak cukup.
- (2) saja cukup,tapi (1) saja tidak cukup.
- Dua pernyataan bersama-sama cukup untuk menjawab pertanyaan, tetapi satu pernyataan saja tidak cukup.
- (1) saja cukup, dan (2) saja cukup.
- (1) dan (2) tidak cukup.
Jawaban: D
Pembahasan:
Bentuk persamaan x2 + bx + 24 = 9 dapat kita ubah menjadi:
x2 + bx + 24 – 9 = 0
x2 + bx + 15 = 0
Dari persamaan kuadrat, diketahui bahwa nilai a = 1, b = ?, c = 15.
Untuk menentukan nilai b, kita dapat menentukan faktor dari hasil a x c = 1 x 15 = 15 terlebih dahulu.
Faktor dari 15 adalah:
1 x 15
-1 x -15
3 x 5
-3 x -5
5 x 3
-5 x -3
15 x 1
-15 x -1
Dari pernyataan 1), diketahui salah satu faktor dari x2 + bx + 26 = 8 adalah (x+5), sehingga faktor yang mungkin adalah 5 x 3.
Jadi, kita dapat menentukan nilai b, yaitu b = 5 + 3 = 8.
Dari pernyatan 2), diketahui salah satu nilai -3 merupakan salah satu akar dari x2 + bx + 26 = 8, sehingga faktor yang mungkin adalah 5 x 3.
Jadi, kita dapat menentukan nilai b yaitu b = 5 + 3 = 8
Kita dapat menyimpulkan bahwa untuk menentukan nilai b, kita dapat menggunakan pernyataan 1) saja atau 2) saja.
Jadi, jawaban yang tepat adalah D
Baca Juga: Contoh Soal Literasi Bahasa Inggris UTBK SNBT 2025 & Pembahasannya

Topik: Aljabar dan Fungsi
Subtopik: Konsep Dasar Persamaan Garis Lurus
29. Diketahui persamaan garis 𝑔 dan ℎ berturut-turut adalah 𝑦 = 3𝑥 + 4 dan 𝑦 = 𝑎𝑥 − 2𝑏. Diketahui pula bahwa garis ℎ memotong sumbu-𝑥 saat 𝑥 = 1. Apakah garis 𝑔 dan ℎ berpotongan di kuadran pertama?
Putuskan apakah pernyataan 1 dan 2 berikut cukup untuk menjawab pertanyaan tersebut.
- Nilai 𝑎 kurang dari negatif 4.
- Nilai 𝑏 kurang dari 0.
- Pernyataan 1 SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan 2 SAJA tidak cukup.
- Pernyataan 2 SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan 1 SAJA tidak cukup.
- DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
- Pernyataan 1 SAJA cukup untuk menjawab pertanyaan dan pernyataan 2 SAJA cukup.
- Pernyataan 1 dan pernyataan 2 tidak cukup untuk menjawab pertanyaan.
Jawaban: A
Pembahasan:
Diketahui bahwa garis ℎ memotong sumbu-𝑥 saat 𝑥 = 1. Artinya, garis ℎ melalui titik (1, 0). Substitusikan titik (1, 0) ke persamaan garis ℎ untuk mendapatkan hubungan 𝑎 dan 𝑏 sebagai berikut.
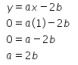
Pernyataan 1: Nilai 𝑎 kurang dari negatif 4.
Jika 𝑎 <− 4, garis ℎ akan turun dari kiri ke kanan dan − 𝑎 > 4 sehingga garis ℎ memotong sumbu-𝑦 di atas garis 𝑦 = 4.
Misal dipilih 𝑎 =− 5, maka garis ℎ melalui titik (1, 0) dan memotong sumbu-𝑦 di titik (0, 5).
Sementara itu, jika disubstitusi 𝑥 =− 1 dan 𝑥 = 0 pada garis 𝑔: 𝑦 = 3𝑥 + 4,, didapat bahwa garis 𝑔 melalui titik (− 1, 1) dan (0, 4).
Akibatnya, garis 𝑔 dan ℎ dapat digambarkan sebagai berikut:
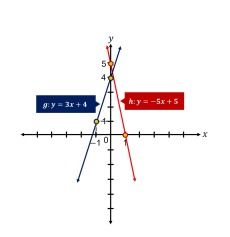
Dapat diperhatikan bahwa kedua garis tersebut berpotongan di kuadran pertama. Oleh karena itu, pernyataan 1 SAJA cukup untuk menjawab pertanyaan.
Pernyataan 2: Nilai 𝑏 kurang dari 0.
Jika 𝑏 < 0, diperoleh bahwa 2𝑏 < 0 sehingga 𝑎 < 0.
Kemudian, jika 𝑎 < 0, garis ℎ akan turun dari kiri ke kanan dan terdapat dua kemungkinan untuk kedudukan titik potong garis ℎ terhadap sumbu-𝑦 sebagai berikut.
- Untuk − 4 < 𝑎 < 0, maka 0 <− 𝑎 < 4 sehingga garis ℎ memotong sumbu-𝑦 di atas sumbu-𝑥 dan di bawah garis 𝑦 = 4. Misal dipilih 𝑎 =− 3, maka garis ℎ melalui titik (1, 0) dan memotong sumbu-𝑦 di titik (0, 3). Akibatnya, garis 𝑔 dan ℎ dapat digambarkan sebagai berikut:
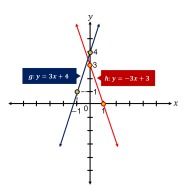
Dapat diperhatikan bahwa kedua garis tersebut berpotongan di kuadran kedua. Oleh karena itu, untuk − 4 < 𝑎 < 0, jawaban dari pertanyaan yang diberikan pada soal adalah garis 𝑔 dan ℎ tidak berpotongan di kuadran pertama.
- Untuk 𝑎 <− 4, maka − 𝑎 > 4 sehingga garis ℎ memotong sumbu-𝑦 di atas garis 𝑦 = 4. Misal dipilih 𝑎 =− 5, maka garis ℎ melalui titik (1, 0) dan memotong sumbu-𝑦 di titik (0, 5). Akibatnya, garis 𝑔 dan ℎ dapat digambarkan sebagai berikut:
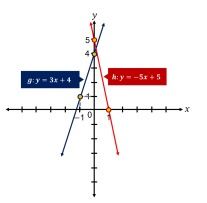
Dapat diperhatikan bahwa kedua garis tersebut berpotongan di kuadran pertama. Oleh karena itu, untuk 𝑎 <− 4, jawaban dari pertanyaan yang diberikan pada soal adalah garis 𝑔 dan ℎ berpotongan di kuadran pertama.
Karena terdapat dua kemungkinan jawaban saat 𝑏 < 0, maka pernyataan 2 SAJA tidak cukup untuk menjawab pertanyaan.
Berdasarkan penjelasan di atas, dapat disimpulkan bahwa pernyataan 1 SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan 2 SAJA tidak cukup.
Jadi, jawaban yang tepat adalah A

Contoh Soal Isian
Topik: Statistika dan Peluang
Subtopik: Konsep Dasar Statistika Deskriptif
30. Diagram batang berikut ini menunjukkan bruto dan neto dari empat jenis produk minuman yang dijual di sebuah toko.
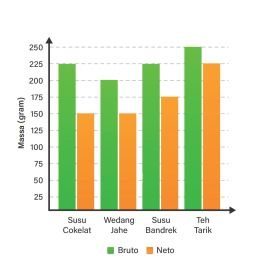
Berdasarkan diagram batang tersebut, rata-rata massa kemasan keempat minuman di atas adalah … gram.
Catatan: Hanya diisi dengan angka (contoh: 10)
Jawaban: 50
Pembahasan:
Besar tara (kemasan) dari setiap produk dapat dihitung dengan cara berikut ini.
- Susu Cokelat
Tara = Bruto – Neto
= 225 – 150
= 75 gram
- Wedang Jahe
Tara = Bruto – Neto
= 225 – 150
= 75 gram
- Susu Bandrek
Tara = Bruto – Neto
= 225 – 175
= 50 gram
- Teh Tarik
Tara = Bruto – Neto
= 250 – 225
= 25 gram


Itu lah beberapa contoh soal TPS UTBK 2025 bagian Pengetahuan Kuantitatif beserta pembahasannya. Semoga, latihan soal ini bisa membantumu dalam mempersiapkan diri untuk menghadapi UTBK nanti, ya! Tetap semangat belajar dan jaga kesehatan.
Kalau kamu mau belajar lebih banyak latihan soal lagi, kamu bisa ikut tryout UTBK SNBT di ruanguji. Di sana, juga ada tips dan trik belajarnya, lho!
















