Latihan Soal Penilaian Tengah Semester 2019: Matematika IPS Kelas XII

Artikel ini memberikan latihan soal beserta pembahasan Penilaian Tengah Semester 2019 matematika IPS kelas 12
—
Apa sih mata pelajaran yang menurut kamu paling sulit? Pasti salah satunya adalah matematika ‘kan? Untuk menguasai seluruh materi matematika di Penilaian Tengah Semester, kamu tentu membutuhkan banyak latihan. Nah tunggu apalagi, ayo langsung saja simak latihan soal beserta pembahasan Penilaian Tengah Semester matematika IPS kelas 12 berikut ini.
Baca juga: Latihan Soal Ujian Nasional SMA 2019 Matematika IPS dan Pembahasannya
-30.png)
Topik: Bidang Datar
Subtopik: Prinsip Kesebangunan
- Perhatikan gambar bangun datar di bawah ini!
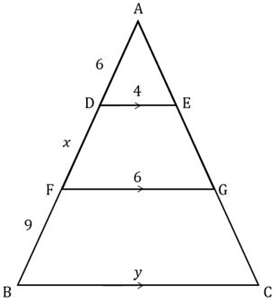
Jika garis DE sejajar garis FG sejajar garis BC maka nilai 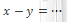
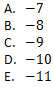
Jawaban: C
Pembahasan:
Perhatikan segitiga ADE sebangun dengan segitiga AFG sehingga diperoleh persamaan:
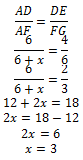
Kemudian perhatikan segitiga ADE sebangun dengan segitiga ABC sehingga diperoleh persamaan :
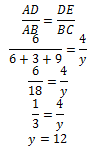
Jadi nilai 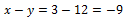
-30.png)
Topik: Bidang Datar
Subtopik: Dalil Dua Garis
2. Perhatikan gambar di bawah ini!
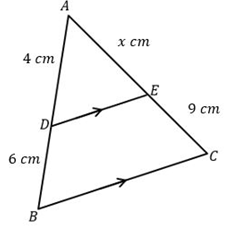
Jika garis DE sejajar dengan garis BC dan panjang AD = 4 cm, BD = 6 cm, AE = x cm dan EC = 9 cm maka nilai dari ![]()
- 8
- 9
- 10
- 12
- 18
Jawaban: D
Pembahasan:
Gunakan dalil intersep untuk gambar pada soal.
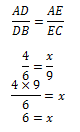
Maka nilai dari 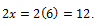
-30.png)
Topik: Bidang Datar
Subtopik: Dalil Menelaus & Dalil Ceva
3. Perhatikan gambar di bawah ini!
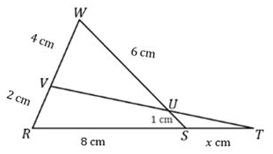
Nilai ![]() yang tepat untuk gambar di atas adalah ….
yang tepat untuk gambar di atas adalah ….
- 2,5
- 3,0
- 3,5
- 4,0
- 4,5
Jawaban: D
Pembahasan:
Gunakan dalil Menelaus untuk gambar pada soal.
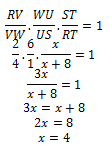
-30.png)
Topik: Bidang Datar
Subtopik: Garis Istimewa Segitiga I
4. Perhatikan gambar berikut ini!
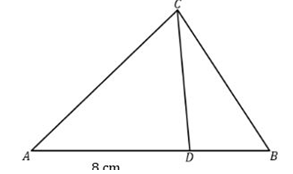
Jika luas segitiga ACD dan BCD berturut-turut adalah ![]() dan
dan ![]() maka panjang BD adalah ….
maka panjang BD adalah ….
- 4,0
- 4,5
- 5,0
- 5,5
- 6,0
Jawaban: D
Pembahasan:
Perhatikan bahwa:
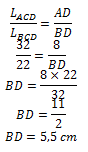
-30.png)
Topik: Bidang Ruang: Kedudukan dan Proyeksi
Subtopik: Ulasan Bangun Ruang
5. Perhatikan bangun ruang di bawah ini.
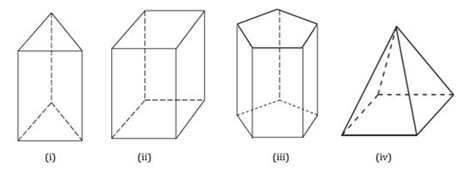
Bangun ruang yang tidak memiliki diagonal ruang adalah ….
- (i) dan (ii)
- (ii) dan (iii)
- (i) dan (iii)
- (ii) dan (iv)
- (i) dan (iv)
Jawaban: E
Pembahasan:
Ingat bahwa diagonal ruang adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan dalam suatu bangun ruang.
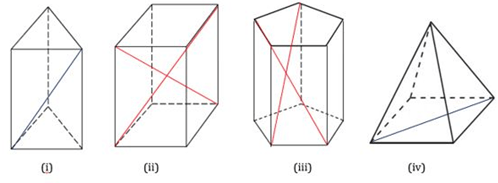
Pada gambar (i) dan (iv) hanya terdapat diagonal sisi saja (garis biru).
-30.png)
Topik: Bidang Ruang: Kedudukan dan Proyeksi
Subtopik: Kedudukan Garis terhadap Garis
6. Garis yang sejajar dengan garis AH adalah….
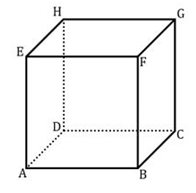
- CF
- EF
- EC
- DC
- CH
Jawaban: A
Pembahasan:
Garis AH berada pada bidang ADHE, sedangkan bidang yang sejajar dengan ADHE adalah bidang BCGF, maka garis yang sejajar dengan bidang AH adalah garis yang berada pada bidang BCGF. Jadi garis AH sejajar dengan CF.
Garis AH bersilangan dengan garis EF, EC dan DC.
Garis AH berpotongan dengan CH di titik H.
-30.png)
Topik: Bidang Ruang: Kedudukan dan Proyeksi
Subtopik: Kedudukan Bidang terhadap Bidang
7. Perhatikan kubus di bawah ini.

Bidang AFH dan bidang BDG adalah bidang yang saling ….
- Sejajar karena memiliki satu garis persekutuan
- Sejajar karena tidak memiliki garis persekutuan
- Berpotongan karena memiliki titik potong
- Berpotongan karena memiliki garis potong
- Bersilangan karena tidak saling bertemu
Jawaban: B
Pembahasan:
Perhatikan gambar kedua bidang tersebut.
Dari gambar di atas maka kedua bidang saling sejajar karena tidak memiliki garis persekutuan.
-30.png)
Topik: Bidang Ruang: Jarak
Subtopik: Jarak Titik ke Titik
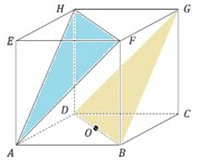
8. Diketahui sebuah kubus ABCD.EFGH dengan rusuk 8 cm seperti pada gambar di bawah ini.

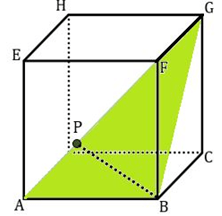
Jika titik P terletak pada garis AG dengan AP : AG = 1 : 4, maka jarak titik B ke titik P adalah ….
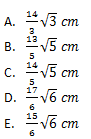
Jawaban: A
Pembahasan:
Perhatikan gambar kubus di bawah ini.
Diketahui rusuk = 8 cm maka,
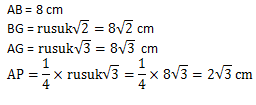
Dari segitiga siku-siku ABG diperoleh :
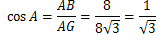
Sedangkan dengan menggunakan aturan cos pada segitiga APB maka diperoleh :
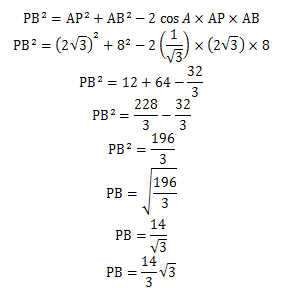
Jadi jarak titik B ke titik P adalah 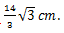
-30.png)
Topik: Bidang Ruang: Jarak
Subtopik: Jarak Titik ke Garis
9. Diketahui kubus ABCD.EFGH dengan rusuk 5 cm seperti gambar di bawah ini. Jarak titik E ke rusuk BC adalah ….

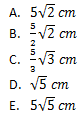
Jawaban: A
Pembahasan:
Perhatikan segitiga EBC pada kubus di bawah ini.
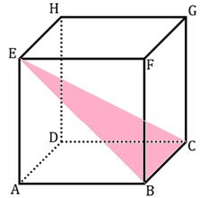
Karena segitiga EBC adalah segitiga siku-siku di B maka jarak terdekat titik E ke garis BC adalah EB 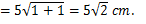
-30.png)
Topik: Bidang Ruang: Jarak
Subtopik: Jarak Dua Garis Bersilangan
10. Diketahui limas T.ABCD dengan alas berbentuk persegi. Rusuk tegak 10 cm dan rusuk alas 8 cm. Jika titik M adalah titik tengah rusuk AD maka jarak garis TM ke garis AB adalah …. Cm
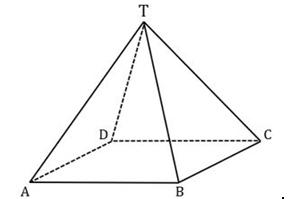
- 2
- 3
- 4
- 5
- 6
Jawaban: C
Pembahasan:
Perhatikan gambar di bawah ini.
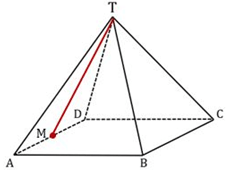
Jika kita buat bidang yang sejajar garis AB dan memuat garis TM yaitu bidang TMN seperti gambar di bawah ini maka jarak
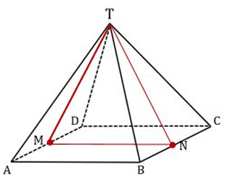
Maka jaraknya berubah jadi jarak garis sejajar bidang.
Misalkan titik P dan Q berturut-turut adalah titik tengah rusuk AB dan garis MN, kemudian proyeksikan titik P ke garis TQ seperti pada gambar di bawah ini.
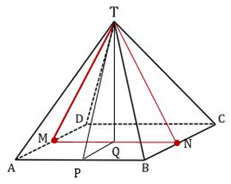
Karena TPQ adalah segitiga siku-siku di Q maka jarak titik P ke garis TQ sama dengan PQ = 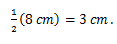
-30.png)
Gimana, penjelasannya mudah dimengerti ‘kan? Mau latihan soal lebih banyak lagi? Buka aja aplikasi Ruangguru karena banyak latihan soal matematika IPS kelas 12 yang bisa kamu kerjakan di ruangbelajar.
![[AB] Web Side Banner - Blog RG](https://cdn-web-2.ruangguru.com/landing-pages/assets/399009fa-feaf-4b6c-8321-92409d53a26a.png)














