Latihan Soal Penilaian Tengah Semester 2019: Matematika IPA Kelas XII

Artikel ini memberikan latihan soal sekaligus pembahasan Penilaian Tengah Semester 2019 mata pelajaran Matematika IPA kelas XII
—
Tak terasa, kamu sudah berada di pertengahan semester ganjil tahun ajaran 2019/2020. Penilaian Tengah Semester (PTS) pun tinggal menghitung hari. Kamu sudah menyiapakan apa saja nih? Apalagi untuk kamu yang duduk di bangku kelas XII. Nilai kamu di PTS ini sangat penting untuk menghadapi SNMPTN sekaligus bisa menjadi persiapan untuk kamu menghadapi ujian-ujian selanjutnya. Ayo, persiapkan diri hadapi PTS dengan latihan soal Matematika IPA kelas XII berikut ini.
Baca juga: Latihan dan Pembahasan Soal UTS Fisika SMA Kelas 12
-24.png)
TOPIK: BIDANG DATAR
SUBTOPIK: DALIL PROYEKSI & DALIL STEWART
- Perhatikan gambar bangun datar di bawah ini!
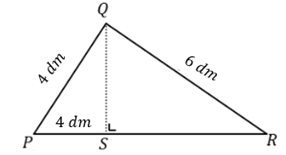
Jika panjang PQ = PS = 4 dm dan QR = 6 dm maka SR = ….
- 5 dm
- 6 dm
- 7 dm
- 8 dm
- 10 dm
Jawaban B
Pembahasan :
Gunakan dalil proyeksi untuk menyelesaikan soal di atas.
Maka,
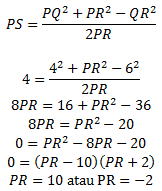
Karena PR menyatakan panjang sisi segitiga maka nilai PR yang memenuhi adalah 10.
Sehingga diperoleh SR = PR – PS = 10 dm – 4 dm = 6 dm.
-24.png)
TOPIK: BIDANG DATAR
SUBTOPIK: GARIS ISTIMEWA SEGITIGA II
2. Perhatikan gambar di bawah ini.
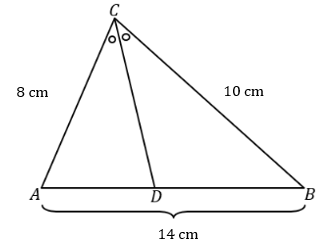
Diketahui garis CD adalah garis bagi segitiga ABC. Panjang CD adalah ….
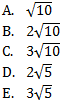
Jawaban B
Pembahasan :
Karena CD adalah garis bagi segitiga ABC, maka
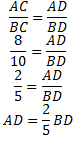
Misalkan 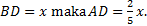
Karena AB = 14 cm, maka
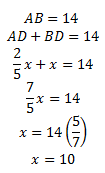
Sehingga BD = 10 cm dan AD = 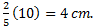
Karena CD adalah garis bagi segitiga ABC, maka
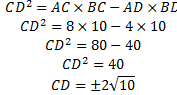
Karena panjang sisi tidak mungkin negatif maka 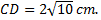
-24.png)
TOPIK: BIDANG RUANG (KEDUDUKAN DAN PROYEKSI)
SUBTOPIK: KEDUDUKAN TITIK
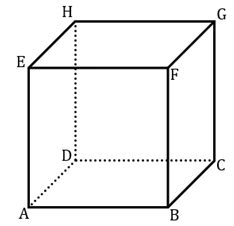
3. Perhatikan kubus ABCD.EFGH di bawah ini.
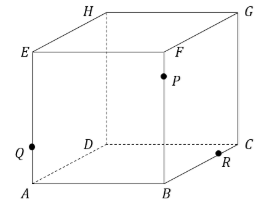
Jika titik P, Q dan R berturut-turut terletak pada rusuk BF, AE dan BC maka pernyataan yang benar adalah ….
- Titik P berada pada bidang CDG
- Titik Q berada pada bidang ABCD
- Titik Q dan R sebidang
- Titik R berada pada bidang ABD
- Titik P, Q dan R sebidang
Jawaban D
Pembahasan :
- Titik P terletak pada bidang ABFE dan bidang BCGF
- Titik Q terletak pada bidang ABFE dan bidang ADHE
- Titik R terletak pada bidang ABCD dan bidang BCGF
- Titik P dan Q sebidang (pada bidang ABFE)
- Titik P dan R sebidang (pada bidang BCGF)
Jadi dari beberapa pernyataan di atas maka pernyataan yang benar pada pilihan jawaban adalah titik R berada pada bidang ABD, karena jika bidang ABD diperluas maka diperoleh bidang ABCD.
-24.png)
TOPIK: BIDANG RUANG (KEDUDUKAN DAN PROYEKSI)
SUBTOPIK: KEDUDUKAN GARIS TERHADAP BIDANG
- Perhatikan kubus ABCD.EFGH di bawah ini.
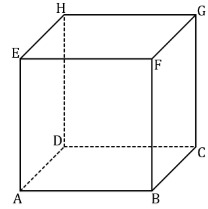
Misalkan P adalah titik tengah ED. Bidang yang tegak lurus dengan garis AP adalah bidang ….
- BCHE
- ADGF
- CDEF
- BDHF
- ABGH
Jawaban C
Pembahasan :
Perhatikan bahwa karena P adalah titik tengah dari diagonal ED maka P juga menjadi titik tengah dari diagonal AH.
Garis AP dapat diperpanjangan menjadi garis AH.
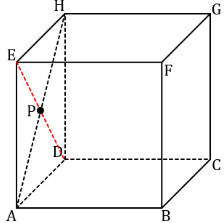
Garis AP dan bidang BCHE
Perhatikan bahwa garis EF terletak pada bidang BCHE. Namun, garis AP tidak tegak lurus garis EH. Sehingga AP tidak tegak lurus bidang BCHE.
Garis AP dengan bidang ADGF
Perhatikan bahwa garis AD terletak pada bidang ADGF. Namun, garis AP tidak tegak lurus dengan garis AD. Sehingga AP tidak tegak lurus bidang ADGF.
Garis AP dan bidang CDEF
Perhatikan gambar di bawah ini.
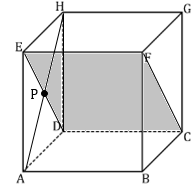
Perhatikan bahwa AH tegak lurus ED maka AP juga tegak lurus ED. Bidang yang memuat ED adalah bidang CDEF. Sehingga garis AP tegak lurus bidang CDEF.
Garis AP dan bidang BDHF
Perhatikan bahwa garis DH berada pada bidang BDHF. Namun, garis AH (sebagai perpanjangan garis AP) tidak tegak lurus garis DH. Sehingga AP tidak tegak lurus bidang BDHF.
Garis AP dan bidang ABGH
Garis AP tidak tegak lurus bidang ABGH karena gari AP terletak pada bidang ABGH.
-24.png)
TOPIK: BIDANG RUANG (KEDUDUKAN DAN PROYEKSI)
SUBTOPIK: PROYEKSI
5. Perhatikan kubus ABCD.EFGH berikut ini.
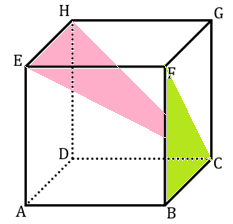
Proyeksi bidang BFC ke bidang CHE adalah bidang….
- BCE
- BCD
- BCM dengan M titik tengan BE
- BCN dengan N titik tengah CH
- BCO dengan O titik tengah EH
Jawaban C
Pembahasan :
Perhatikan gambar di bawah ini.

Bidang BFC jika diperluas maka akan menjadi bidang BCHE. Garis potong bidang BCHE dengan bidang BCE adalah garis BC. Kemudian proyeksikan titik F ke bidang BCHE.
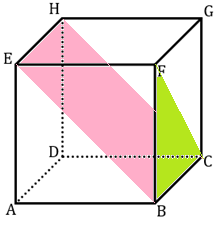
Misalkan titik M adalah titik potong diagonal sisi BE dan diagonal sisi AF. Maka titik M berada tepat pada pertengahan garis BE.
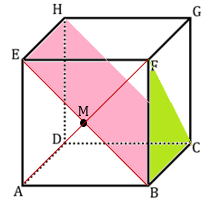
Ingat kembali bahwa diagonal sisi pada kubus saling tegak lurus. Sehingga, proyeksi titik F ke bidang BCHE sama dengan proyeksi titik F ke garis BE, yaitu titik M.
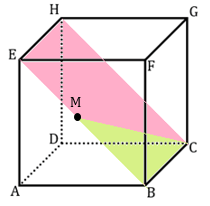
Jadi proyeksi bidang BCF ke bidang BCHE adalah bidang BCM dimana M adalah titik tengah BE.
-24.png)
TOPIK: BIDANG RUANG (JARAK)
SUBTOPIK: JARAK TITIK KE BIDANG
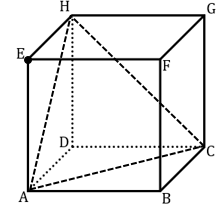
6. Diketahui sebuah kubus ABCD.EFGH dengan rusuk 6 cm. Jarak titik E ke bidang ACH adalah …. cm.
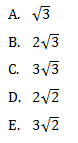
JAWABAN : B
PEMBAHASAN :
Jika kita tambahkan satu buah kubus lagi disebelah kiri kubus ABCD.EFGH kemudian perluas bidang ACH seperti pada gambar berikut ini.
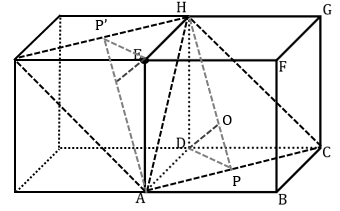
Sehingga jarak titik E ke bidang ACH sama dengan jarak titik E ke garis AP’, atau sama juga dengan jarak titik D ke titik O.
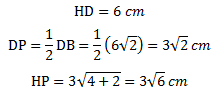
Sehingga dengan persamaan luas segitiga DHP diperoleh :
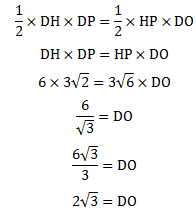
Jadi Jarak titik E ke bidang ACH adalah 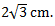
-24.png)
TOPIK: BIDANG RUANG (JARAK)
SUBTOPIK: JARAK DUA BIDANG SEJAJAR
7. Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm. Jarak bidang ACH dengan bidang BEG adalah …. cm
JAWABAN : A
PEMBAHASAN :
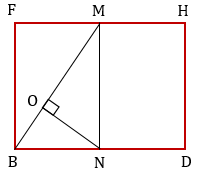
Untuk memudahkan buat bidang diagonal BDHF dengan titik M dan titik N adalah titik tengah perpotongan diagonal atap dan alas seperti gambar berikut.
Bidang BEG berptongan dengan bidang BDHF di garis BM. Sedangkan bidang ACH berpotongan dengan bidang BDHF di garis HN.
Jika kita buat segitiga BMN pada bidang diagonal BDHF maka jarak bidang ACH ke bidang BEG sama dengan jarak titik N ke garis BM atau sama dengan NO.
Dengan persamaan luas segitiga BMN maka diperoleh :
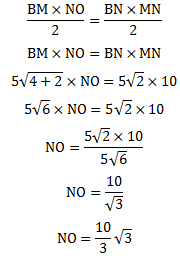
Jadi jarak bidang ACH ke bidang BEG adalah 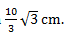
-24.png)
TOPIK: BIDANG RUANG (SUDUT)
SUBTOPIK: SUDUT DUA GARIS
8. Diketahui kubus ABCH.EFGH dengan rusuk 4 cm. Titik T membagi dua rusuk BC menjadi dua bagian. Jika ![]() adalah sudut antara garis HT dengan garis BG maka
adalah sudut antara garis HT dengan garis BG maka 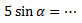
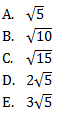
Jawaban C
Pembahasan :
Perhatikan kubus di bawah :
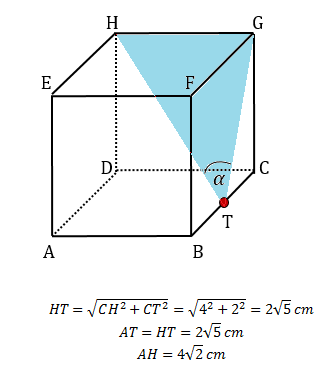
Kemudian pada segitiga ATH, misalkan R adalah titik pada AH sehingga garis TR tegak lurus garis AH.
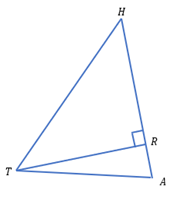
Dengan aturan cos maka diperoleh,
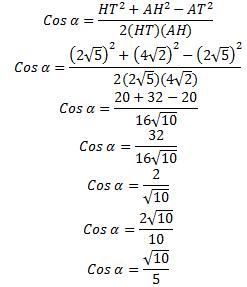
Kemudian hitung nilai sin ![]() dengan rumus identitas trigonometri berikut :
dengan rumus identitas trigonometri berikut :
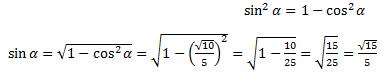
Jadi nilai dari 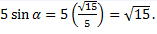
-24.png)
TOPIK: BIDANG RUANG (SUDUT)
SUBTOPIK: SUDUT GARIS DAN BIDANG
9. Diketahui sebuah kubus ABCD.EFGH dengan panjang sisi kubus ![]() . Sinus sudut antara rusuk BF ke bidang BEG adalah….
. Sinus sudut antara rusuk BF ke bidang BEG adalah….
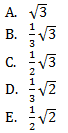
Jawaban B
Pembahasan :
Perhatikan gambar di bawah ini.
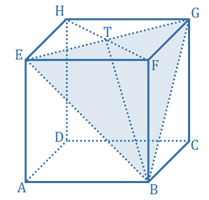
Diketahui :
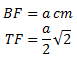
Sehingga,
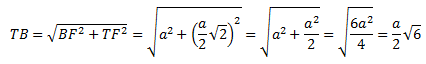
Maka,
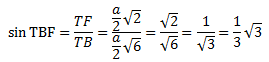
Sinus sudut antara rusuk BF ke bidang BEG adalah ![]()
-24.png)
TOPIK: BIDANG RUANG (SUDUT)
SUBTOPIK: IRISAN BIDANG
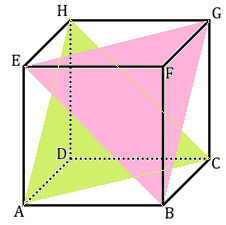
10. Diketahui kubus ABCD.EFGH dengan titik M adalah titik tengah rusuk CG. Irisan bidang yang melalu titik M, D dan F adalah ….
- Segitiga
- Segitiga sama sisi
- Segiempat
- Segilima
- Persegi
Jawaban C
Pembahasan :
Perhatikan gambar di bawah ini.
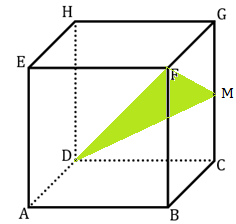
Karena titik D terletak pada rusuk yang bersebrangan dengan titik F maka titik M akan berseberangan pula dengan titik lain di rusuk AE. Misalkan titik N adalah titik tengah rusuk AE.
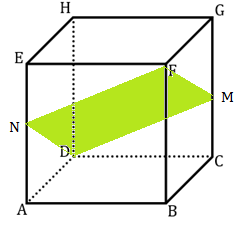
Sehingga bidang yang terbentuk adalah bidang segiempat NDFM seperti pada gambar di atas.
-24.png)
Gimana, membantu ‘kan? Mau latihan lebih banyak soal? Yuk, latihan soal-soal terkait materi ujian sekolah di ruangbelajar.
![[AB] Web Side Banner - Blog RG](https://cdn-web-2.ruangguru.com/landing-pages/assets/399009fa-feaf-4b6c-8321-92409d53a26a.png)














