Latihan Soal HOTS SBMPTN dan Pembahasan 2019: Matematika IPA

Artikel ini memberikan latihan soal HOTS SBMPTN dan pembahasan 2019 materi Matematika IPA untuk siswa yang akan menghadapi SBMPTN
—
Squad, salah satu cara paling ampuh untuk menaklukan SBMPTN adalah bersahabat dengan soal-soal HOTS. Tunggu apa lagi? Yuk, simak latihan dan pembahasan soal HOTS SBMPTN Matematika Dasar 2019 berikut.
-11.png)
Topik: Trigonometri
Subtopik: Periode dan Nilai Maksimum/Minimum Fungsi Trigonometri
1. Jika fungsi F(x) = a2 cos (ax) – 7 memiliki periode ![]() , maka nilai minimum fungsi F adalah … .
, maka nilai minimum fungsi F adalah … .
- − 16
- – 6
- 1
- 6
- 9
Jawaban: A
Pembahasan:
- nilai a pada fungsi diperoleh dari rumus
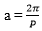 di mana P adalah periode grafik
di mana P adalah periode grafik
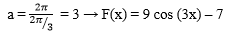
- karena −1 ≤ cos 3x ≤ 1 maka nilai minimum F tercapai saat cos 3x = −1
F = 9(−1) – 7 = −16
-11.png)
Topik: Transformasi Geometri
Subtopik: Komposisi Transformasi Titik (Refleksi, Translasi)
2. Diketahui gradien garis yang melalui titik O(0,0) dan P(a,b) adalah −2. Jika P dicerminkan terhadap sumbu X kemudian digeser 5 satuan ke bawah dan 1 satuan ke kiri, maka gradien garis yang melalui P’ dan O(0,0) adalah 3. Titik P adalah … .
- (−2,4)
- (−1,2)
- (1,−2)
- (2,−4)
- (3,−6)
Jawaban: A
Pembahasan:
- Gradien garis yang melalui P(a,b) dan O(0,0) adalah
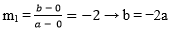
- P(a,b) dicerminkan terhadap sumbu X menjadi (a,−b)
- Pergeseran senilai 1 satuan ke kiri dan 5 satuan ke bawah adalah
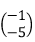
- Titik (a,−b) digeser oleh
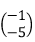 menjadi P’(a – 1, −b – 5)
menjadi P’(a – 1, −b – 5) - Gradien garis yang melalui P’ dan O(0,0) adalah
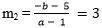
−b – 5 = 3a – 3
2a – 5 = 3a – 3
a = −2 dan b = 4
- Titik P(−2,4)
-11.png)
Topik: Dimensi Tiga
Subtopik: Panjang Proyeksi
3. Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Jika titik P di tengah-tengah AB dan titik Q di tengah-tengah BC, maka jarak titik H dengan garis PQ adalah … .
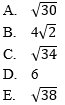
Jawaban: C
Pembahasan:

-11.png)
Topik: Limit
Subtopik: Limit Fungsi Aljabar dan Trigonometri
4. Nilai 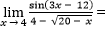 … .
… .
- −24
- −6
- 0
- 6
- 24
Jawaban: E
Pembahasan:
Dikalikan dengan bentuk sekawan penyebut:
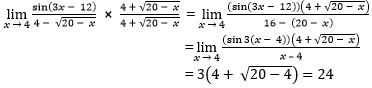
-11.png)
Topik: Barisan dan Deret
Subtopik: Barisan dan Deret Geometri
5. Jika sin α, cos α, ![]() membentuk barisan geometri, maka jumlah 8 suku pertamanya adalah … .
membentuk barisan geometri, maka jumlah 8 suku pertamanya adalah … .

Jawaban: B
Pembahasan:
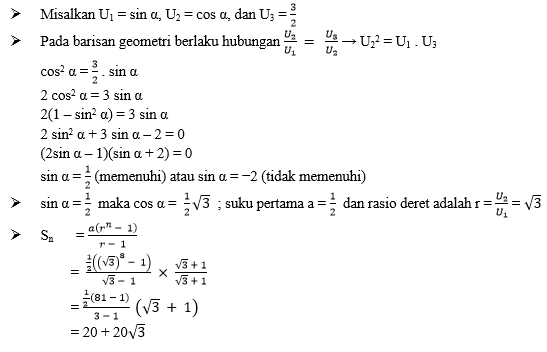
-11.png)
Topik: Integral
Subtopik: Volume Benda Putar
6. Volume benda putar daerah yang dibatasi y = 1 + x2, y = 9 – x2, dan sumbu Y diputar mengelilingi sumbu X adalah … .

Jawaban: D
Pembahasan:
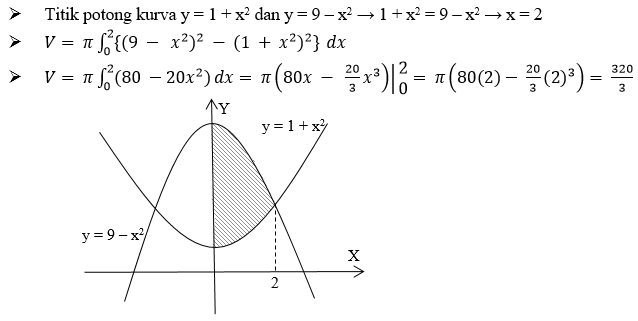
-11.png)
Topik: Teori Peluang
Subtopik: Kaidah Pencacahan
7. Suatu sekolah membentuk tim delegasi yang terdiri dari 6 siswa kelas X, 5 siswa kelas XI, dan 4 siswa kelas XII. Kemudian akan ditentukan pimpinan yang terdiri dari Ketua, Sekretaris, dan Jika kelas asal ketua harus lebih tinggi dari kelas asal sekretaris dan bendahara, maka banyak kemungkinan susunan pimpinan adalah … .
- 156
- 492
- 546
- 590
- 720
Jawaban: D
Pembahasan:
- Terdapat dua kemungkinan susunan pimpinan yaitu siswa kelas XII sebagai ketua atau siswa kelas XI sebagai ketua
- Bila kelas XII sebagai ketua = 4 ⨯ 11 ⨯ 10 = 440
- Bila kelas XI sebagai ketua = 5 ⨯ 6 ⨯ 5 = 150
- Total kemungkinan adalah = 440 + 150 = 590 cara
-11.png)
Topik: Lingkaran
Subtopik: Persamaan Lingkaran
8. Jika panjang jari-jari lingkaran x2 + y2 + Ax + 2Ay + C = 0 dan x2 + y2 + Ax + 3Ay + C = 0 adalah 5 dan 3 , maka nilai C = … .
- −1
- −2
- −3
- −4
- −5
Jawaban: E
Pembahasan:
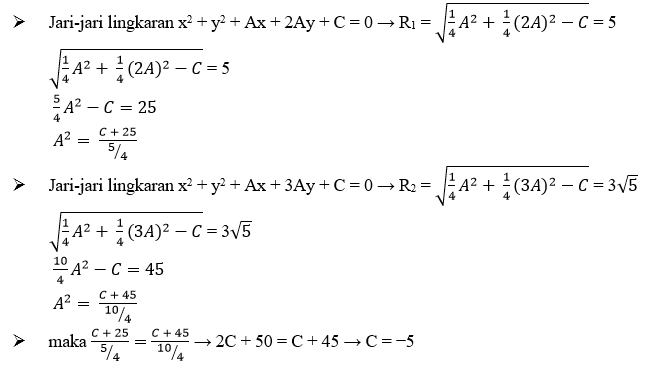
-11.png)
Topik: Polinomial
Subtopik: Teorema Sisa
9. Sisa pembagian F(x) = x3 + ax2 + 4x + 5b + 1 oleh x2 + 4 adalah a – 4. F(x) dibagi oleh x + 1 bersisa −27. Nilai a – 2b = … .
- 5
- 4
- 3
- 2
- 1
Jawaban: A
Pembahasan:
- F(x) dibagi x + 1 bersisa −27 → F(x) = (x + 1) . H1(x) + (−27) di mana H1 adalah hasil bagi
F(−1) = (−1)3 + a(−1)2 + 4(−1) + 5b + 1 = −27
5b + 1 = −22 – a
- F(x) dibagi x2 + 4 bersisa a – 4 → F(x) = (x2 + 4)(x – k) + (a – 4)
x3 + ax2 + 4x + 5b + 1 = x3 – kx2 + 4x – 4k + a – 4 maka terdapat hubungan:
a = −k dan 5b + 1 = −4k + a – 4
a = −k dan −22 – a = −4k + a – 4
−22 – a = −4(−a) + a – 4
a = −3 dan b = −4
- maka a – 2b = 5
-11.png)
Topik: Turunan
Subtopik: Persamaan Garis Singgung
10. Grafik 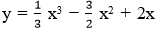 memiliki garis singgung mendatar pada titik P dan Q. Jumlah ordinat titik P dan Q adalah … .
memiliki garis singgung mendatar pada titik P dan Q. Jumlah ordinat titik P dan Q adalah … .
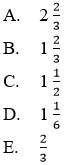
Jawaban: C
Pembahasan:
- Garis singgung mendatar memiliki gradien sama dengan nol, maka F’(x) = 0
F’(x) = x2 – 3x + 2 = 0
(x – 1)(x – 2) = 0
x1 = 1 atau x2 = 2
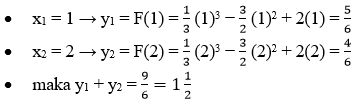
-11.png)
Ingin latihan soal Matematika lebih banyak lagi? Yuk, nonton video beranimasi, video pembahasan soal SBMPTN, latihan soal, dan rangkuman infografis di ruangbelajar.
















