Info Penting Komposisi Transformasi | Matematika Kelas 12

Squad, kalian pernah nggak sih berkeinginan untuk melakukan transformasi? Misalnya, bertransformasi menjadi orang lain. Atau kalian ingin punya robot-robot keren seperti yang ada di film transformers? Hmm.. sepertinya sebelum kalian berkeinginan terlalu jauh, lebih baik kalian belajar tentang komposisi transformasi pada matematika dulu nih. Wah, matematika punya komponen transformasi juga? Penasaran, kan? Kuy, kita belajar bersama!

Keren banget, ya! (Sumber: kaskus.co.id)

Sekarang kita mulai belajar komposisi transformasi pada matematika, ya. Semoga semenarik transformers favoritmu. Hehehe. Oke deh, jadi tahap awal untuk memahami komposisi transformasi ini, kamu harus mengingat bahwa jika T₁ dan T₂ masing-masing merupakan transformasi yang bersesuaian dengan kondisi-kondisi yang kayak gini:

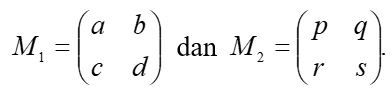berarti, komposisi transformasi dinyatakan dengan T_2 º T₁ dan bersesuaian dengan matriks ini, nih:

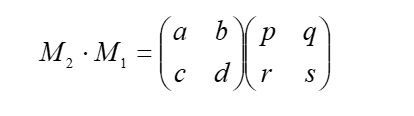
Hmm…. lalu komposisi transformasi itu banyak jenisnya nggak, sih? Ada beberapa jenis komposisi transformasi, tetapi yang kita bahas di artikel ini 2 dulu ya! 2 jenis komposisi transformasi yang akan dibahas kali ini yaitu komposisi dua translasi berurutan dan komposisi dua refleksi berurutan.

Komposisi Dua Translasi Berurutan

Untuk komposisi transformasi jenis ini, kamu akan menggunakan rumus komutatif, nih. Wah, itu rumus yang seperti apa, sih? Jadi, pada komposisi dua translasi berurutan, pasti pada awalnya diketahui terlebih dahulu 2 kondisi ini:

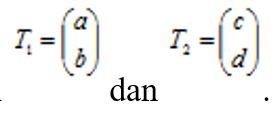
Nah, setelah itu, jika translasi T₁ dilanjutkan translasi T₂, maka kemudian akan dinotasikan dengan “^{T_1 º T₂} ” dengan translasi tunggal T=T₁+T₂=T₂+T₁ yang merupakan sifat komutatif. Jangan pusing dulu ya, masih ada 1 jenis lagi yang akan kita bahas, nih. 

Komposisi Dua Refleksi Berurutan

Sekarang kita lanjut ke komposisi dua refleksi berurutan, ya! Salah satu contoh yang bisa diambil pada kondisi ini adalah refleksi berurutan terhadap 2 sumbu sejajar. Jadi, jika titik A(x,y) direfleksikan terhadap garis x=a dilanjutkan terhadap garis x=b. Maka bayangan akhir A adalah , yang dijelaskan dengan kondisi berikut: x’=2(b-a)+x dan y’=y. 

Tapi kalau titik tersebut direfleksikan terhadap garis y=a gimana dong? Bisa juga nggak, sih? Bisa, kok! Kalau titik A(x,y) direfleksikan terhadap garis y=a, dan dilanjutkan terhadap garis y=b, maka bayangan akhir A adalah  yaitu: x’=x dan y’=2(b-a)+y. Jangan tertukar-tukar, ya!

—

Wah, ternyata komposisi transformasi ini punya beberapa bentuk, ya. Semoga setelah baca artikel ini kalian nggak jadi makin bingung, ya. Nah Squad, kalian masih ingin tahu lebih banyak? Punya pertanyaan? Bingung mau tanya ke mana?

Yuk, tanya lewat guru-guru di Ruangguru Privat Matematika! Para pengajar di Ruangguru Privat juga sudah terstandarisasi kualitasnya, loh. Kamu juga bisa pilih nih, mau diajarkan secara langsung (offline) atau daring (online). Fleksibel, kan? Untuk info lebih lanjut, cuss klik link berikut! Selamat belajar!

Sumber Referensi:

Wirodikromo, S. dan Darmanto, M. (2019) Matematika untuk SMA/MA Kelas XI kelompok Wajib 2. Jakarta:Erlangga

Sumber Gambar:

Foto ‘Transformer’ [Daring]. Tautan: https://www.kaskus.co.id/thread/589ed0a031e2e6b5228b4567/trailer-keren-film-hollywood-terbaru/2 (Diakses: 9 Desember 2020)

Foto ‘Jangan pusing dulu, ya!‘ [Daring]. Tautan: https://www.wellspringrenewalcenter.com/quick-tips-for-teachers-parents-of-kids-who-dont-do-transitions/ (Diakses 9 Desember 2020)

Artikel diperbaharui 9 Desember 2020