Apa Saja Hubungan Dua Sudut dan Antarsudut? | Matematika Kelas 7

Setelah kita belajar tentang properti dan macam-macam sudut, kali ini, yuk kita perdalam materi dengan mengetahui hubungan antarsudut. Ada apa aja ya? Simak selengkapnya di artikel Matematika kelas 7 berikut ya!

—

Kamu tau nggak, ternyata sudut-sudut itu punya hubungan lho. Iya benar hubungan. Hubungannya bukan sudut A ternyata adiknya dari sudut B. Bukan juga sudut C itu merupakan ayah dari sudut D, ya. Kalau itu sih bukan hubungan dalam sudut, tapi hubungan keluarga yang digambarkan dengan perumpamaan sudut-sudut. Hehehe…

Lalu, seperti apa hubungan-hubungan dalam sudut itu?

Jadi begini, hubungan dalam sudut itu ada dua. Pertama hubungan dua sudut dan yang kedua hubungan antarsudut. Sekarang kita bahas satu per satu ya!

Macam-Macam Hubungan Dua Sudut

Kamu jangan membayangkan hubungan dua sudut itu seperti hubungan seperti Dilan dan Milea ya. Hubungan dua sudut dalam Matematika ini mudah dan nggak berat kok seperti yang dikatakan Dilan.

Kalau rindu itu memang berat, biarkan saja Dilan yang merasakan. Tapi, kata Dilan tadi hubungan dua sudut itu mudah kok. Jadi, nggak perlu ngebayangin kalau hubungan dua sudut itu bakalan sulit.

Kembali ke hubungan dua sudut, ya. Ada 3 macam sudut yang masuk ke dalam pembahasan hubungan dua sudut.

Baca Juga: Mengenal Macam-Macam Sudut, Gambar & Ciri-Cirinya

1. Sudut yang Saling Berpelurus (Bersuplemen)

Nah, sudut berpelurus  atau yang disebut juga dengan sudut yang saling bersuplemen, maksudnya bukan sudut yang memiliki vitamin ya. Jangan mentang-mentang ada kata “suplemen” lalu kamu kaitin sama vitamin. Ini nggak ada kaitannya sama sekali.

Sudut berpelurus itu sudut yang seperti gambar berikut:

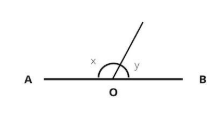
 Gambar sudut berpelurus. (Sumber: Adjar.id)

Berpelurus diambil dari kata lurus. Nah, garis lurus itu besar sudutnya ialah 180°, jadi garis lurus dari titik A ke titik B dengan membentuk ∠AOB besarnya ialah 180°.

Sekarang, coba perhatikan garis AB. Di titik O dibuat garis melalui C, dan terbentuk ∠AOC dan ∠BOC. ∠AOC ini merupakan sudut berpelurus dari ∠BOC, karena jumlah dari ∠AOC + ∠BOC = 180°.

Dengan kata lain, dua sudut dikatakan berpelurus jika jumlah kedua sudutnya 180°.

2. Sudut yang Saling Berpenyiku (Berkomplemen)

Kamu pasti tahu kan besar sudut siku-siku itu 90°. Nah, konsepnya sama dengan sudut berpenyiku. Sudut berpenyiku itu sudut yang seperti gambar berikut:

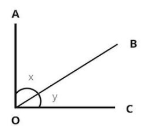
 Gambar sudut berpelurus. (Sumber: Adjar.id)

Dua sudut dikatakan sudut berpenyiku jika jumlah kedua sudutnya ialah 90°. Coba kamu perhatikan titik A ke titik C. Ada titik O yang membentuk ∠AOB besarnya ialah 90°. Di titik O dibuat garis melalui B, dan terbentuk ∠AOB dan ∠BOC.

Kalau sudut berpelurus jika dijumlahkan sudut-sudutnya akan berjumlah 180°, maka untuk sudut berpenyiku jika ∠AOC + ∠BOC = 90°.

Baca Juga: Apa Saja Bagian-Bagian dari Properti Sudut?

3. Sudut yang Saling Bertolak Belakang

Kalau kamu penggemar sepak bola pasti tidak asing dengan Cristiano Ronaldo dan Lionel Messi bukan. Coba perhatikan tendangan Cristiano Ronaldo berikut.

(sumber: giphy.com)

Lalu, kalau kamu penggemar Lionel Messi, pasti tidak asing dengan gol-gol Messi yang seperti ini.

(sumber: giphy.com)

Sekarang coba temukan hal yang bertolak belakang dari kedua tendangan pemain sepakbola tersebut?

Yap. Bener banget. Kaki yang digunakan Cristiano Ronaldo dan Messi berbeda. Ronaldo menggunakan kaki kanan untuk mencetak gol, Messi menggunakan kaki kiri.

Sangat bertolak belakang bukan kaki yang digunakan untuk mencetak gol?

Adakah hubungannya dengan sudut yang kita pelajari?

Oh tentu tidak. Itu tadi hanya perumpamaan saja kok. Sudut yang bertolak belakang itu sudut yang arah hadapnya berlawanan. Kalau kamu sulit membayangkan, gambarannya itu seperti kamu kalau lagi berdebat dengan orangtua kamu. Ayah kamu punya pendapat A, tapi kamu punya pendapat B.

Perlu kamu ingat nih, besarnya sudut yang bertolak belakang ini sama lho ya.

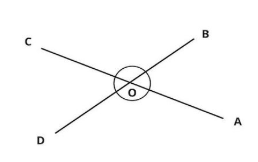
 Gambar sudut bertolak belakang. (Sumber: Adjar.id)

Garis AC dan BD itu garis lurus yang berpotongan di titik O, sehingga terbentuk pasangan. ∠AOD dan ∠BOC atau ∠AOB dan ∠COD. Nah, pasangan sudut-sudut tersebut itulah yang disebut dengan sudut yang bertolak belakang.

Sudut yang saling bertolak belakang itu sama besar. Apabila dijumlahkan, semua sudutnya akan membentuk satu lingkaran atau putaran yaitu 360°. Mudahnya, itu dapat dipahami seperti ini.

1. ∠AOC dan ∠BOD saling bertolak belakang, sehingga ∠AOC = ∠BOD

2. ∠BOC dan ∠AOD saling bertolak belakang, sehingga ∠BOC = ∠AOD

Baca Juga: Cara Menghitung Keliling dan Luas Segitiga

Nah, setelah mengetahui hubungan dua sudut, sekarang kita lanjut yuk membahas tentang hubungan antarsudut.

“Hmmm…kayaknya bakalan lebih sulit ya?”

Enggak kok. Asal kamu benar-benar mencermati tulisan di artikel ini. Stay focus, ya.

Macam-Macam Hubungan Antarsudut

Hubungan antarsudut itu nggak seperti hubungan antarnegara yang saling bekerja sama ya. Kalau hubungan antarnegara itu dipersatukan oleh kesamaan visi dan misi, kalau hubungan antarsudut itu dipisahkan atau dipotong oleh garis lain.

Yups, dipotong oleh garis lain. Perhatikan gambar berikut:

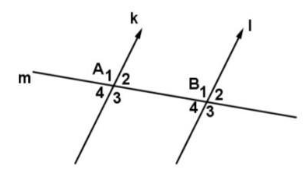
Garis k // l dipotong oleh garis m dititik A dan B, maka akan terjadi sudut-sudut berikut:

1. Sudut-Sudut Sehadap

Coba perhatikan ∠A4 dan ∠B4 menghadap ke arah yang sama kan? Menghadap ke arah kiri bawah. Sudut seperti ∠A4 dan ∠B4 disebut sudut-sudut sehadap.

Ada pun pasangan sudut-sudut sehadap yang lain adalah ∠A1 dan ∠B1 , ∠A2 dan ∠B2 dan ∠A3 dan ∠B3.

2. Sudut-Sudut Dalam Berseberangan

Sudut dalam bersebrangan itu ialah ∠A3 dan ∠B1, terletak berseberangan yang dibatasi garis m dan berada di bagian dalam antara garis k dan l.

Sudut-sudut seperti ∠A3 dan ∠B1 disebut sudut-sudut dalam berseberangan. Sudut dalam berseberangan yang lain adalah ∠A2 dan ∠B4.

3. Sudut-Sudut Luar Berseberangan

Selain sudut dalam bersebrangan, ada juga sudut luar bersebrangan nih. ∠A1 dan ∠B3 terletak berseberangan yang dibatasi garis m dan berada di bagian luar garis k dan l.

Sudut-sudut seperti ∠A1 dan ∠B3 disebut sudut-sudut luar berseberangan. Sudut luar berseberangan yang lain adalah ∠A4 dan ∠B2.

4. Sudut-Sudut Dalam Sepihak

∠A3 dan ∠B4 terletak pada pihak yang sama, yaitu bagian bawah garis m dan berada di bagian dalam antara garis k dan l.

Sudut-sudut seperti ∠A1 dan ∠B3 disebut sudut-sudut dalam sepihak. Sudut dalam sepihak yang lain adalah ∠A2 dan ∠B1 karena terletak pada pihak yang sama (di atas).

Baca Juga: Serba-Serbi Segitiga: Garis, Sudut & Bangun Istimewa

5. Sudut-Sudut Luar Sepihak

∠A4 dan ∠B3 terletak pada pihak yang sama, yaitu bagian bawah garis m dan berada di bagian luar garis k dan l.

Sudut-sudut seperti ∠A4 dan ∠B3 disebut sudut-sudut luar. Sudut luar sepihak yang lain adalah ∠A1 dan ∠B2 karena terletak pada pihak yang sama (di atas).

—

Kamu masih merasa bingung dengan penjelasan tentang hubungan dua sudut dan antarsudut tadi? Jangan khawatir. Coba gabung di ruangbelajar yuk. Ada video belajar dengan animasi yang keren banget lho. Soal latihan dan rangkumannya juga banyak, dijamin bikin belajar kamu jadi lebih mudah.

Sumber Gambar:

‘GIF Tendangan Messi’ [Daring]. Tautan: https://giphy.com/gifs/messi-goal-fk-8cyro9Vo2FNhZ5mucq (Diakses pada 4 Februari 2025)

‘GIF Tendangan Ronaldo’ [Daring]. Tautan: https://giphy.com/gifs/cristiano-ronaldo-hd-2014-5C6ZE1ehlCuze (Diakses pada 4 Februari 2025)

http://adjar.grid.id/read/543243848/hubungan-antarsudut-sudut-berpelurus-berpenyiku-dan-bertolak-belakang?page=all (Diakses pada 4 Februari 2024)