Diagram Venn: Karakteristik, Bentuk & Cara Pengoperasian | Matematika Kelas 7
Di artikel Matematika kelas 7 ini, kita akan membahas tentang diagram venn, mulai dari karakteristik, bentuk-bentuk, dan cara pengoperasiannya dalam bentuk contoh soal. Yuk, kita pelajari bersama!
—
Teman-teman, kamu sudah baca belum artikel tentang istilah-istilah dalam himpunan? Kalo belum, coba deh baca dulu. Nah, pada artikel kali ini, kita akan mempelajari materi lanjutan dari materi tersebut, yaitu diagram venn. Apa sih diagram venn itu?
Mengenal Diagram Venn
Diagram venn adalah suatu gambar yang digunakan untuk menyatakan hubungan antar dua himpunan atau lebih dalam himpunan semesta. Hmm bingung, ya? Supaya nggak bingung, kita mulai mengingat lagi mengenai pengertian himpunan dulu, deh. Himpunan adalah kumpulan objek yang dapat didefinisikan dengan jelas dan terukur, sehingga dapat diketahui termasuk atau tidaknya di dalam himpunan tertentu.
Nah, diagram venn ini bertugas untuk menggambarkan hubungan antar himpunan tadi ke dalam sebuah diagram agar lebih mudah dipahami.
Karakteristik Diagram Venn
Nah, dalam membuat diagram venn ini, nggak bisa sembarangan, teman-teman. Ada aturan atau ketentuan dalam pembuatannya. Lalu, apa saja ya aturan itu? Kamu bisa lihat gambar mengenai karakteristik diagram venn di bawah ini, ya!
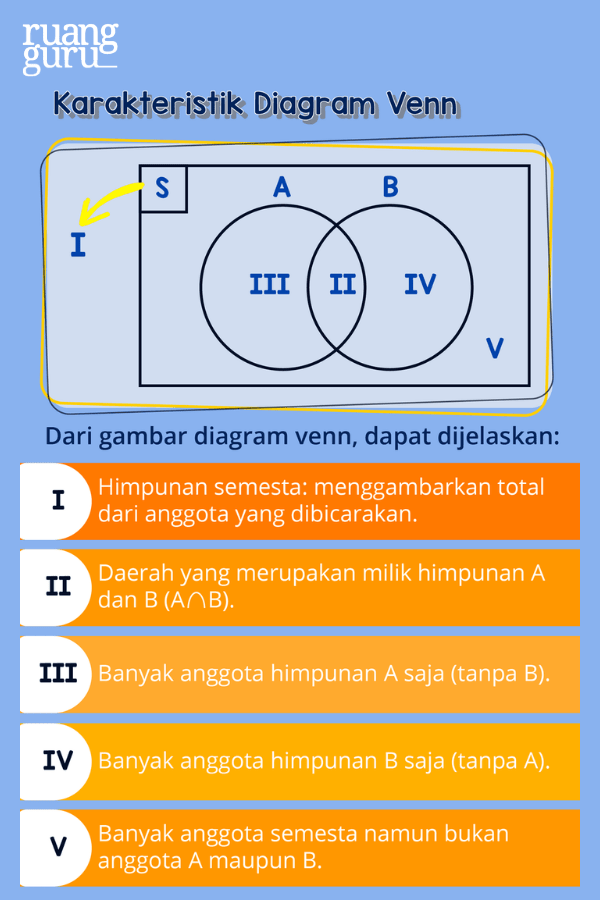
Ada 3 ketentuan di dalam membuat diagram venn, yaitu:
1. Himpunan semesta (S): biasanya digambarkan dengan persegi panjang dan lambang S ditulis pada sudut kiri atas gambar persegi panjang.
2. Setiap himpunan lain yang dibicarakan (selain himpunan kosong) digambarkan dengan lingkaran (kurva tertutup).
3. Setiap anggota ditunjukkan dengan noktah (titik) dan anggota himpunan ditulis di samping noktah tersebut.
Baca Juga: Hubungan Antar Himpunan Matematika dan Contohnya
Jadi inget ya, kalo di diagram venn itu ada kotak persegi panjang dengan lambang S, lingkaran pertama yang nunjukkin himpunan 1, dan lingkaran kedua yang nunjukkin himpunan 2. Nah, sekarang kita pelajari beberapa bentuk-bentuk diagram venn. Check this out!
Macam-Macam Bentuk Diagram Venn
Kamu masih inget nggak nih, himpunan terbagi menjadi berbagai macam jenis. Oleh karena itu, diagram venn juga bisa terdiri dari berbagai macam bentuk, di antaranya:
1. Himpunan yang Berpotongan
Himpunan yang pertama adalah himpunan yang berpotongan. Himpunan yang berpotongan adalah jika ada anggota himpunan A dan B yang sama. Jadi anggota yang masuk ke dalam himpunan A juga ternyata masuk ke himpunan B. Himpunan A berpotongan dengan himpunan B dapat ditulis A∩B. Bingung ya? Gini loh maksudnya.
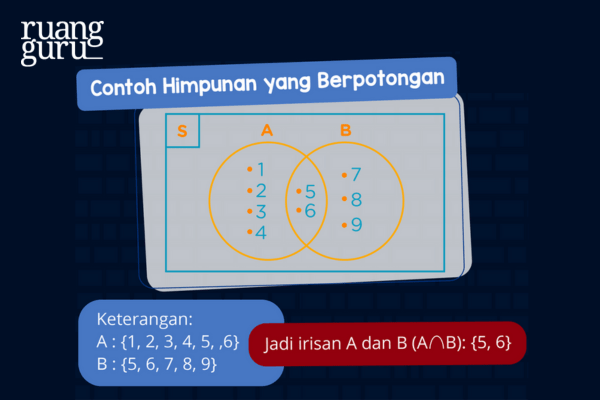
2. Himpunan Saling Lepas
Selanjutnya, himpunan saling lepas. Himpunan A dan B dikatakan saling lepas jika tidak ada anggota himpunan A dan B yang sama. Himpunan A saling lepas dengan himpunan B dapat ditulis sebagai A//B. Nah, bentuk diagram venn-nya kaya gini, ya!
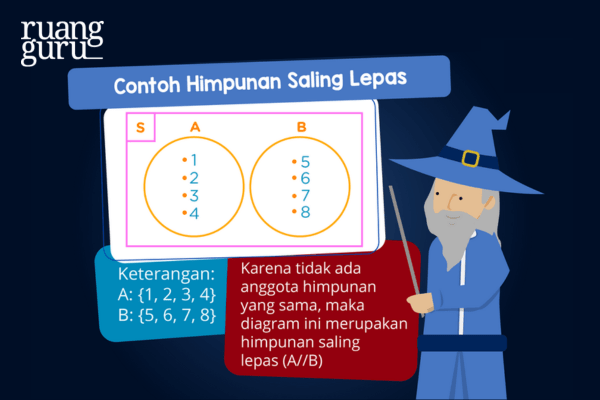
Gimana? Lanjut nggak, nih? Jangan sampe bingung ya bedain bentuk diagram venn-nya. Lanjut kuy.
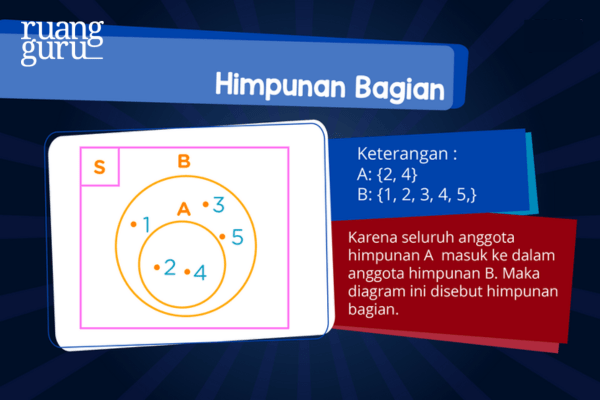
3. Himpunan Bagian
Himpunan yang ketiga adalah himpunan bagian. Himpunan A dapat dikatakan himpunan bagian dari himpunan B jika semua anggota himpunan A merupakan anggota dari himpunan B. Untuk lebih mudahnya di ilustrasikan seperti berikut ini:
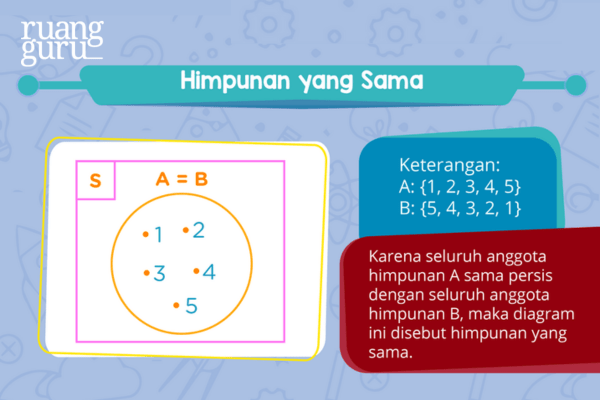
4. Himpunan yang Sama
Himpunan yang sama dapat dinyatakan jika setiap anggota A merupakan anggota B dan setiap anggota B merupakan anggota A. Misalnya A = {1, 2, 3, 4, 5} dan B = {5, 4, 3, 2, 1}. Nah anggota kedua himpunan ini sama persis kan? Jadi dapat dikatakan himpunan A sama dengan himpunan B. Himpunan yang sama ini dapat ditulis A = B.
Contoh Soal Diagram Venn
Nah sekarang udah mulai paham kan tentang diagram venn? Sekarang kita coba contoh soalnya yuk. Perhatikan gambar di bawah ini ya!
Contoh Soal 1
Dalam penelitian yang dilakukan oleh sekelompok siswa di kelasnya, dipeoleh data 18 orang sarapan dengan nasi, 5 orang sarapan dengan roti, dan 3 orang sarapan nasi dan roti, sedangkan 4 orang sarapannya tidak dengan nasi ataupun roti. Hitunglah banyaknya siswa dalam kelas tersebut!
Pembahasan:
Kita bisa menggunakan diagram ven untuk menjawab soal tersebut. Jika kita gambarkan dengan diagram ven, maka gambarnya akan seperti berikut ini.
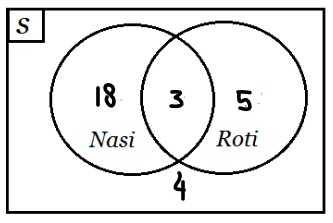
Kamu harus paham bahwa sebanyak 3 siswa yang sarapan dengan nasi dan roti, termasuk ke dalam 18 siswa yang sarapan dengan nasi dan 5 siswa yang sarapan dengan roti. Artinya, kamu harus mencari banyaknya siswa yang sarapan dengan nasi dan roti saja. Untuk mencarinya, kamu bisa menggunakan cara:
Banyak siswa yang sarapan dengan nasi saja = Banyak siswa yang sarapan dengan nasi – Banyak siswa yang sarapan dengan nasi dan roti = 18 – 3 = 15
Banyak siswa yang sarapan dengan roti saja = Banyak siswa yang sarapan dengan roti – Banyak siswa yang sarapan dengan nasi dan roti = 5 – 3 = 2
Dengan demikian, banyaknya siswa dalam kelas tersebut dapat kita hitung dengan cara:
Banyak siswa = Banyak siswa yang tidak sarapan dengan nasi dan roti + Banyak siswa yang sarapan dengan nasi dan roti + Banyak siswa yang sarapan dengan nasi + Banyak siswa yang sarapan dengan roti
Banyak siswa = 4 + 3 + 15 + 2 = 24 siswa.
Contoh Soal 2
Dari beberapa anak remaja, diketahui 25 orang suka minum susu, 20 orang suka minum kopi, dan 12 orang suka susu dan kopi. Dari data di atas, jawablah pertanyaan di bawah ini.
a. jumlah semua anak remaja
b. jumlah remaja yang suka susu saja
c. jumlah remaja yang suka kopi saja
d. jumlah remaja yang suka kedua-duanya
Pembahasan:
Ingat, ya! Sebanyak 12 remaja yang suka minum susu dan kopi itu, termasuk ke dalam 25 remaja yang suka minum susu dan 12 remaja yang suka minum kopi. Jadi, kamu cari dulu banyak remaja yang suka minum susu saja, dan banyak remaja yang suka minum kopi saja, dengan cara:
Banyak remaja suka minum susu = 25 – 12 = 13
Banyak remaja suka minum kopi = 20 – 12 = 8
Sehingga, jika digambarkan, maka bentuk diagram venn-nya menjadi seperti berikut ini:
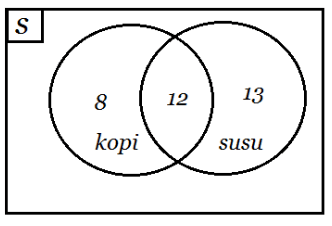
a. Jumlah semua anak remaja = 8 + 12 + 13 = 33 orang
b. Jumlah remaja yang suka susu saja = 13 orang
c. Jumlah remaja yang suka kopi saja = 8 orang
d. Jumlah remaja yang suka kedua-duanya = 12 orang
Oke, itulah pembahasan mengenai diagram venn, mulai dari karakteristik, macam-macam bentuk, hingga contohnya. Gimana? Udah paham belum tentang diagram venn. Nah untuk mempelajari materi-materi lainnya. yuk belajar dengan ruangbelajar. Dijamin belajar kamu bakalan semakin seru dengan soal-soal pembahasan yang ada. Jangan lupa download ya!
Referensi:
As’ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017) Matematika SMP/MTs Kelas VII Semester I. Pusat Kurikulum dan Perbukuan, Balitbang, Kemendikbud
Artikel diperbarui pada 19 September 2023.














