Contoh Soal Penalaran Matematika UTBK-SNBT 2025

Yuk, lihat kumpulan contoh soal Penalaran Matematika UTBK yang akan diujikan pada SNBT 2025 beserta pembahasannya berikut ini.
—
Kali ini, kita akan membahas contoh soal Tes Literasi SNBT UTBK untuk salah satu subtesnya, yaitu Penalaran Matematika. Yuk, langsung aja kita pelajari!
Apa itu Tes Penalaran Matematika?
Tes Penalaran Matematika adalah tes yang akan mengukur kemampuan calon mahasiswa untuk menerapkan matematika dasar dalam kehidupan sehari-hari. Penalaran Matematika juga merupakan salah satu subtes di UTBK 2025.
Namun, kamu nggak hanya akan mengerjakan hitung-hitungan biasa, guys. Soal-soal yang diberikan pada tipe tes Penalaran Matematika ini akan menguji kamu, tidak hanya pada penguasaan materi atau rumus saja, tetapi juga pada penggunaan penalaran, konsep, fakta, dan alat matematika dalam pemecahan masalah sehari-hari.
Jumlah Soal dan Materi Tes Penalaran Matematika
Tes Penalaran Matematika terdiri dari 20 soal dengan waktu pengerjaan selama 30 menit. Berikut beberapa kisi-kisi materi yang akan diujikan dalam Tes Penalaran Matematika:
- Bilangan
- Bilangan (Representasi, Sifat Urutan, Operasi Hitung)
- Himpunan
- Pola Bilangan
- Aljabar dan Fungsi
- Bentuk Aljabar
- Aritmetika Sosial
- Perbandingan dan Rasio
- Persamaan Garis Lurus
- Fungsi
- Persamaan dan Pertidaksamaan
- Pengukuran dan Geometri
- Garis dan Sudut
- Bangun Datar
- Bangun Ruang
- Data dan Ketidakpastian
- Statistika Desktriptif
- Aturan Pencacahan
- Teori Peluang
Untuk bisa memecahkan soal-soal Penalaran Matematika, hal pertama yang kamu lakukan adalah berdoa, teliti dan tetap tenang. Mulailah mengerjakan soal dari yang paling mudah dulu dan jangan terlalu fokus pada satu soal saja.
Contoh Soal Penalaran Matematika UTBK SNBT 2025
Yuk, mulai berlatih dari sekarang dengan contoh soal UTBK berikut ini:
1. Topik: Menghitung Luas Ruangan
Perhatikan ilustrasi berikut!
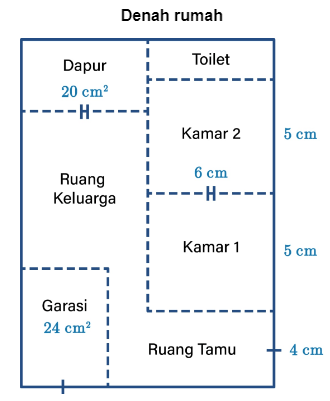
Gambar di atas menunjukkan denah rumah Anton dengan skala 1:100. Diketahui luas bangunan sebenarnya adalah 12 m x 16 m. Setiap ruangan kecuali ruang keluarga dan ruang tamu berbentuk persegi panjang. Kemudian, diketahui pula luas setiap kamar sama.
Luas toilet rumah Anton sebenarnya adalah ….

Jawaban: B
Pembahasan:
Diketahui luas bangunan sebenarnya adalah 12 m x 16 m atau dapat ditulis 1.200 cm x 1.600 cm. Karena skala yang digunakan adalah 1:100, maka luas bangunan pada denah tersebut adalah 12 cm x 16 cm.
Selanjutnya, berdasarkan informasi pada teks, didapat gambar sebagai berikut.
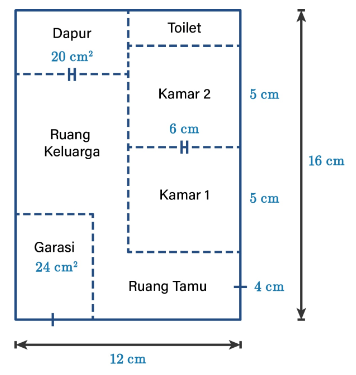
Dapat diperhatikan bahwa panjang toilet pada denah tersebut adalah 6 cm. Artinya, panjang toilet sebenarnya adalah 100⋅6 cm = 600 cm.
Kemudian, lebar toilet pada denah tersebut adalah 16 – 5 – 5 – 4 = 2 cm. Artinya, lebar toilet sebenarnya adalah 100⋅2 cm = 200 cm.
Dengan demikian, luas toilet sebenarnya adalah sebagai berikut.
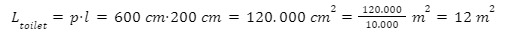
Jadi, jawaban yang tepat adalah B.

2. Topik: Menghitung Total Luas Ruangan
Perhatikan ilustrasi berikut!

Gambar di atas menunjukkan denah rumah Anton dengan skala 1:100. Diketahui luas bangunan sebenarnya adalah 12 m x 16 m. Setiap ruangan kecuali ruang keluarga dan ruang tamu berbentuk persegi panjang. Kemudian, diketahui pula luas setiap kamar sama.
Total luas ruang tamu dan luas ruang keluarga pada denah adalah … ![]() .
.
- 76
- 82
- 94
- 110
- 116
Jawaban: A
Pembahasan:
Diketahui luas bangunan sebenarnya adalah 12 m x 16 m atau dapat ditulis 1.200 cm x 1.600 cm. Karena skala yang digunakan adalah 1:100, maka luas bangunan pada denah tersebut adalah 12 cm x 16 cm = 192 ![]() .
.
Selanjutnya, berdasarkan informasi pada teks, didapat gambar sebagai berikut.

Misalkan A menyatakan jumlah luas kamar 1, kamar 2, dan toilet sehingga didapat perhitungan sebagai berikut.
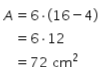
Dengan demikian, total luas ruang tamu dan luas ruang keluarga pada denah tersebut dapat dihitung sebagai berikut.
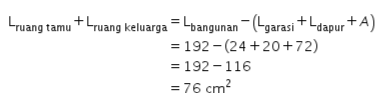
Jadi, jawaban yang tepat adalah A.

3. Topik: Total Biaya Berdasarkan Luas Ruangan
Perhatikan ilustrasi berikut!
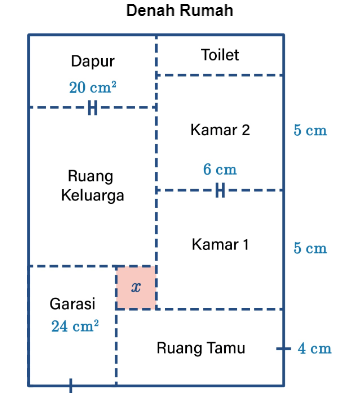
Gambar di atas menunjukan denah rumah Anton dengan skala 1:100. Diketahui luas bangunan sebenarnya adalah 12 m x 16 m. Setiap ruangan kecuali ruang keluarga dan ruang tamu berbentuk persegi panjang.
Anton hendak memasang karpet pada daerah berwarna biru yang diberi label X. Jika harga karpet tersebut adalah Rp120.000,00 per ![]() , total biaya yang dibutuhkan Anton untuk membeli karpet tersebut adalah ….
, total biaya yang dibutuhkan Anton untuk membeli karpet tersebut adalah ….
- Rp120.000,00
- Rp200.000,00
- Rp240.000,00
- Rp400.000,00
- Rp480.000,00
Jawaban: E
Pembahasan:
Dapat diperhatikan pada denah tersebut bahwa garasinya memiliki luas 24 ![]() . Karena panjang garasi adalah 4 cm, maka lebar garasi tersebut adalah
. Karena panjang garasi adalah 4 cm, maka lebar garasi tersebut adalah ![]() = 6 cm. Akibatnya, lebar daerah X pada denah adalah 6 – 4 = 2 cm.
= 6 cm. Akibatnya, lebar daerah X pada denah adalah 6 – 4 = 2 cm.
Kemudian, diketahui panjang kamar pada denah tersebut adalah 6 cm. Karena panjang bangunan pada denah adalah 12 m, maka panjang daerah pada denah X adalah 12 – 6 – 4 = 2 cm.
Karena skala denah tersebut adalah 1:100, maka panjang dan lebar daerah X sebenarnya masing-masing adalah 100⋅2 cm=200 cm=2 m.
Diketahui harga karpet tersebut adalah Rp120.000,00 per ![]() . Akibatnya, total biaya yang dibutuhkan Anton untuk membeli karpet tersebut adalah sebagai berikut.
. Akibatnya, total biaya yang dibutuhkan Anton untuk membeli karpet tersebut adalah sebagai berikut.

Jadi, jawaban yang tepat adalah E.
Baca Juga: Contoh Soal Tes Skolastik Literasi Bahasa Indonesia UTBK/SNBT 2025 serta Pembahasannya

4. Topik: Selisih
Perhatikan ilustrasi berikut!
Kelompok Belajar
Suatu kelompok belajar terdiri dari siswa laki-laki dan siswa perempuan. Salah satu siswa laki-laki bernama Edo dan salah satu siswa perempuan bernama Tari. Banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki.
Selisih banyaknya siswa laki-laki dan perempuan di kelompok belajar tersebut adalah … siswa.
- 0
- 1
- 2
- 3
- 4
Jawaban: C
Pembahasan:
Misalkan banyak siswa laki-laki di kelompok tersebut adalah x dan banyak siswa perempuan di kelompok tersebut adalah y.
Diketahui banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki. Oleh karena itu, dapat dibuat persamaan sebagai berikut.
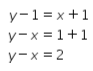
Dengan demikian, selisih banyaknya siswa laki-laki dan perempuan di kelompok belajar tersebut adalah 2 siswa.
Jadi, jawaban yang tepat adalah C.

5. Topik: Menghitung Jumlah Siswa
Perhatikan ilustrasi berikut!
Kelompok Belajar
Suatu kelompok belajar terdiri dari siswa laki-laki dan siswa perempuan. Salah satu siswa laki-laki bernama Edo dan salah satu siswa perempuan bernama Tari. Banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki.
Jumlah seluruh siswa di kelompok belajar tersebut adalah … siswa.
- 3
- 4
- 6
- 7
- 10
Jawaban: E
Pembahasan:
Misalkan banyak siswa laki-laki di kelompok tersebut adalah x dan banyak siswa perempuan di kelompok tersebut adalah y.
Diketahui banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Artinya, dapat dibuat persamaan berikut.
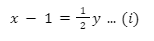
Kemudian, diketahui banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki. Artinya, dapat dibuat persamaan berikut.
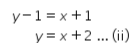
Substitusikan persamaan ii ke persamaan i sehingga didapat nilai x sebagai berikut.
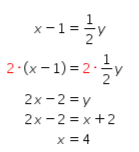
Substitusikan nilai x = 4 ke persamaan ii sehingga didapat nilai y sebagai berikut.
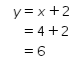
Didapat bahwa banyak siswa laki-laki dan perempuan di kelompok belajar tersebut secara berurutan adalah 4 dan 6.
Dengan demikian, jumlah seluruh siswa di kelompok belajar tersebut adalah 4 + 6 = 10 siswa.
Jadi, jawaban yang tepat adalah E.

Sampai sini, sudah mulai panas belum? Tenang-tenang, regangkan badan, minum air putih, kita break sebentar sambil menonton penjelasan Tes Skolastik Penalaran Matematika dari kakak-kakak Master Teacher Ruangguru berikut ini!
6. Topik: Perbandingan Jumlah Siswa
Perhatikan ilustrasi berikut!
Kelompok Belajar
Suatu kelompok belajar terdiri dari siswa laki-laki dan siswa perempuan. Salah satu siswa laki-laki bernama Edo dan salah satu siswa perempuan bernama Tari. Banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki.
Jika siswa laki-laki bertambah 1 dan siswa perempuan berkurang 1, perbandingan banyak siswa laki-laki dan perempuan di kelompok tersebut adalah ….
- 1:1
- 1:2
- 2:1
- 2:3
- 3:4
Jawaban: A
Pembahasan:
Misalkan banyak siswa laki-laki di kelompok tersebut adalah x dan banyak siswa perempuan di kelompok tersebut adalah y.
Diketahui banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Artinya, dapat dibuat persamaan berikut.
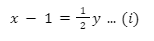
Kemudian, diketahui banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki. Artinya, dapat dibuat persamaan berikut.
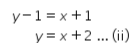
Substitusikan persamaan ii ke persamaan i sehingga didapat nilai x sebagai berikut.
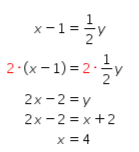
Substitusikan nilai x = 4 ke persamaan ii sehingga didapat nilai y sebagai berikut.
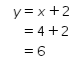
Didapat bahwa banyak siswa laki-laki dan perempuan di kelompok belajar tersebut secara berurutan adalah 4 dan 6.
- Jika siswa laki-laki bertambah 1, banyak siswa laki-laki menjadi 4 + 1 = 5 siswa.
- Jika siswa perempuan berkurang 1, banyak siswa perempuan menjadi 6 – 1 = 5 siswa.
Dengan demikian, perbandingan banyak siswa laki-laki dan perempuan di kelompok tersebut adalah 5:5 = 1:1.
Jadi, jawaban yang tepat adalah A.

7. Topik: Peluang
Perhatikan ilustrasi berikut!
Kelompok Belajar
Suatu kelompok belajar terdiri dari siswa laki-laki dan siswa perempuan. Salah satu siswa laki-laki bernama Edo dan salah satu siswa perempuan bernama Tari. Banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki.
Banyak cara memilih 2 orang siswa jika setidaknya terpilih 1 orang siswa laki-laki adalah ….
- 6
- 12
- 24
- 30
- 36
Jawaban: D
Pembahasan:
Misalkan banyak siswa laki-laki di kelompok tersebut adalah x dan banyak siswa perempuan di kelompok tersebut adalah y.
Diketahui banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Artinya, dapat dibuat persamaan berikut.
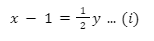
Kemudian, diketahui banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki. Artinya, dapat dibuat persamaan berikut.
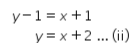
Substitusikan persamaan ii ke persamaan i sehingga didapat nilai x sebagai berikut.
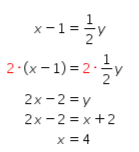
Substitusikan nilai x = 4 ke persamaan ii sehingga didapat nilai y sebagai berikut.
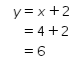
Didapat bahwa banyak siswa laki-laki dan perempuan di kelompok belajar tersebut secara berurutan adalah 4 dan 6.
Selanjutnya, akan dipilih 2 orang siswa dengan syarat terpilih setidaknya 1 orang siswa laki-laki. Dalam hal ini, akan terdapat dua kasus sebagai berikut.
Kasus 1: Terpilih 1 siswa laki-laki dan 1 siswa perempuan.
Banyak cara memilih 2 orang siswa pada kasus ini dapat dihitung sebagai berikut.
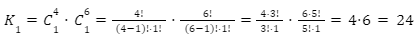
Kasus 2: Terpilih 2 siswa laki-laki.
Banyak cara memilih 2 orang siswa pada kasus ini dapat dihitung sebagai berikut.
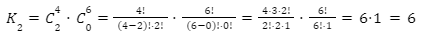
Perhatikan bahwa kejadian memilih siswa pada kasus 1 dan kasus 2 tidak mungkin terjadi secara bersamaan. Artinya, kejadian memilih siswa ini merupakan kejadian saling lepas. Oleh karena itu, total banyak cara memilih 2 orang siswa tersebut dapat dihitung menggunakan aturan penjumlahan, yaitu 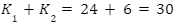 cara.
cara.
Jadi, jawaban yang tepat adalah D.
Baca Juga: Contoh Soal Tes Skolastik Literasi Bahasa Inggris UTBK/SNBT 2025 serta Pembahasannya

8. Topik: Pendapatan Maksimum
Perhatikan ilustrasi berikut!
Bianglala
Sebuah bianglala di taman hiburan memiliki 36 kabin penumpang. Setiap kabin hanya boleh diisi oleh 2 orang dewasa atau 1 orang dewasa dan 2 anak-anak. Berikut adalah daftar harga tiket bianglala tersebut.
- Senin–Jumat: anak-anak Rp20.000,00 dan dewasa Rp30.000,00
- Sabtu, Minggu, dan Hari libur: anak-anak Rp35.000,00 dan dewasa Rp50.000,00
Jika pada jam 18.30 di hari Minggu setengah kabin diisi oleh anak-anak dan seluruh kabin tidak ada yang kosong, jumlah pendapatan maksimum taman hiburan dari bianglala yang mungkin diperoleh pada saat itu adalah ….
- Rp1.260.000,00
- Rp2.340.000,00
- Rp2.700.000,00
- Rp2.610.000,00
- Rp3.960.000,00
Jawaban: E
Pembahasan:
Berdasarkan informasi pada soal, disebutkan bahwa kondisinya adalah sebagai berikut.
Hari Minggu, maka harga tiket anak-anak Rp35.000,00 dan dewasa Rp50.000,00.
Setengah kabin (18 kabin) diisi anak-anak = tidak boleh ada kabin yang hanya diisi anak-anak, maka harus ada orang dewasa. Karena yang ditanyakan adalah pendapatan maksimum, maka digunakan asumsi sejumlah 18 kabin diisi 1 dewasa dan 2 anak-anak.
Seluruh kabin tidak ada yang kosong, maka 18 kabin sisanya diisi oleh 2 orang dewasa.
Pendapatan maksimum yang mungkin diperoleh dapat diketahui dengan perhitungan berikut

Berdasarkan hasil perhitungan tersebut, dapat diketahui bahwa jumlah pendapatan maksimum taman hiburan dari bianglala yang mungkin diperoleh pada saat itu adalah Rp3.960.000,00.
Jadi, jawaban yang tepat adalah E.

9. Topik: Menghitung Jumlah dalam Suatu Rentang Waktu
Perhatikan teks berikut!
Data Covid-19 Tahun 2022
Per 1 September 2020, Indonesia telah melaporkan 177.571 kasus positif COVID-19, dengan catatan sebanyak 42.009 dirawat/isolasi mandiri, 128.057 sembuh, dan 7.505 meninggal. Case fatality ratio (CFR) adalah proporsi individu terkonfirmasi penyakit yang meninggal karena penyakit tersebut. Berikut merupakan data perkembangan kasus pasien COVID-19.
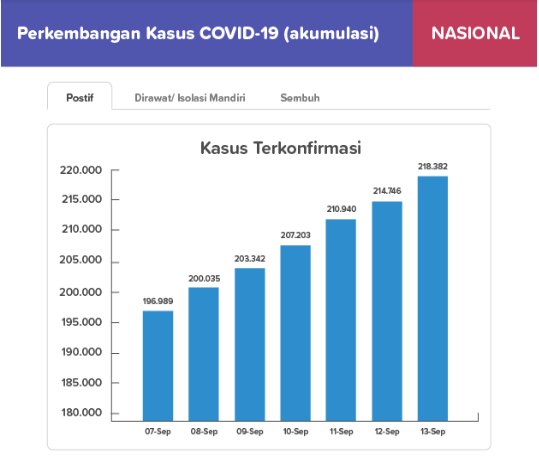
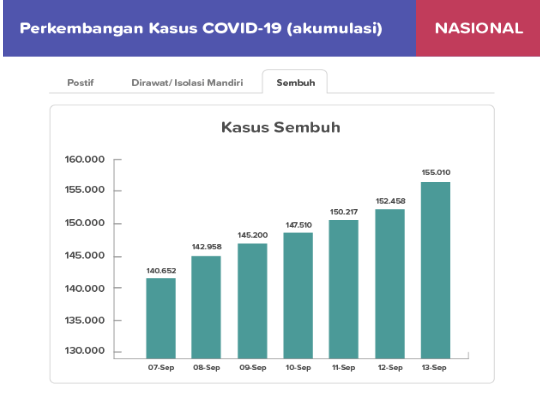
Penambahan kasus terkonfirmasi tertinggi terjadi pada rentang tanggal ….
- 7 September – 8 September
- 9 September – 10 September
- 10 September – 11 September
- 11 September – 12 September
- 12 September – 13 September
Jawaban: B
Pembahasan:
Berdasarkan informasi pada soal dapat diketahui jumlah kasus terkonfirmasi adalah sebagai berikut.
- 7 September 2020 = 196.989
- 8 September 2020 = 200.035
- 9 September 2020 = 203.342
- 10 September 2020 = 207.203
- 11 September 2020 = 210.940
- 12 September 2020 = 214.746
- 13 September 2020 = 218.382
Penambahan kasus terkonfirmasi pada rentang tanggal 7 September – 8 September
= 200.035 – 196.989 = 3.046
Penambahan kasus terkonfirmasi pada rentang tanggal 9 September – 10 September
= 207.203 – 203.342 = 3.861
Penambahan kasus terkonfirmasi pada rentang tanggal 10 September – 11 September
= 210.940 – 207.203 = 3.737
Penambahan kasus terkonfirmasi pada rentang tanggal 11 September – 12 September
= 214.746 – 210.940 = 3.806
Penambahan kasus terkonfirmasi pada rentang tanggal 12 September – 13 September
= 218.382 – 214.746 = 3.636
Berdasarkan hasil perhitungan tersebut, dapat diketahui bahwa penambahan kasus terkonfirmasi terbesar berada pada rentang tanggal 9 September – 10 September, yakni sebanyak 3.861.
Jadi, jawaban yang tepat adalah B.

10. Topik: Menghitung Jumlah dalam Suatu Rentang Waktu
Perhatikan teks berikut!
Data Covid-19 Tahun 2022
Per 1 September 2020, Indonesia telah melaporkan 177.571 kasus positif COVID-19, dengan catatan sebanyak 42.009 dirawat/isolasi mandiri, 128.057 sembuh, dan 7.505 meninggal. Case fatality ratio (CFR) adalah proporsi individu terkonfirmasi penyakit yang meninggal karena penyakit tersebut. Berikut merupakan data perkembangan kasus pasien COVID-19.


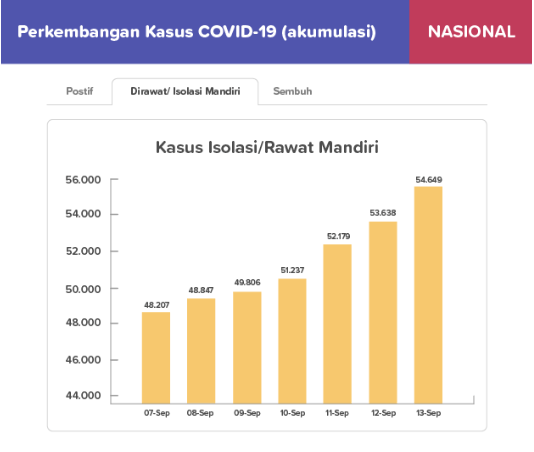
Jangkauan data berdasarkan grafik kasus sembuh pada rentang tanggal 7 September 2020 – 13 September 2020 adalah ….
- 14.358
- 25.552
- 140.652
- 152.458
- 155.010
Jawaban: A
Pembahasan:
Data terendah = 140.652
Data tertinggi = 155.010
Jangkauan data adalah selisih data dengan nilai terbesar dan nilai terkecil.
Jangkauan data = data tertinggi – data terendah
Jangkauan data = 155.010 – 140.652
Jangkauan data = 14.358
Jadi, jawaban yang tepat adalah A.
Baca Juga: Kumpulan Contoh Soal Tes Skolastik UTBK/SNBT 2025 & Pembahasannya

11. Topik: Bilangan
Subtopik: Konsep Kilat Operasi Hitung Bilangan
Perhatikan ilustrasi berikut!
Anggun membawa tiga buah barang, yaitu A, B, dan C yang beratnya berturut-turut 1.450 g, 0,5 kg, dan 3,2 kg ke WahAda Cargo untuk dikirimkan ke Cimahi. Berikut ini tabel yang menunjukkan biaya pengiriman barang.
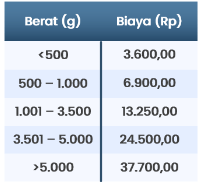
Apabila terdapat potongan harga sebesar 10% untuk setiap pengiriman barang, total biaya yang dikeluarkan Anggun untuk mengirimkan barang A, B, dan C secara terpisah adalah ….
- Rp28.060,00
- Rp30.060,00
- Rp33.400,00
- Rp35.490,00
- Rp37.700,00
Jawaban: B
Pembahasan:
Diketahui bahwa barang A seberat 1.450 g barang B seberat 0,5 kg = 500 g dan barang C seberat 3,2 g = 3.200 g.
Total biaya yang dikeluarkan untuk mengirimkan barang A, B, dan C secara terpisah dapat dihitung sebagai berikut.
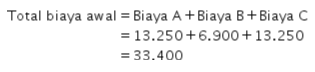
Karena setiap pengiriman barang akan mendapatkan potongan harga sebesar , maka biaya yang dikeluarkan Anggun menjadi sebagai berikut.
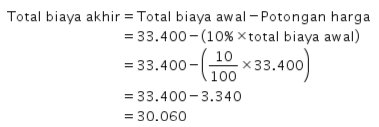
Dengan demikian, total biaya yang dikeluarkan Anggun untuk mengirimkan barang A, B, dan C secara terpisah adalah Rp30.060,00.

12. Topik: Bilangan
Subtopik: Konsep Kilat Operasi Hitung Bilangan
Perhatikan notasi atom berikut ini!
![]()
Y: lambang atom
A: nomor massa
Z: nomor atom atau jumlah proton
Isoton adalah atom-atom yang memiliki jumlah neutron sama banyak. Jumlah neutron dapat dihitung dengan menggunakan persamaan berikut.
![]()
Isoton dari atom ![]() adalah ….
adalah ….
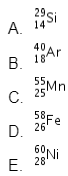
Jawaban: C
Pembahasan:
Pada soal, diketahui persamaan sebagai berikut.
![]()
Dari persamaan tersebut, didapat bahwa jumlah neutron bisa dihitung sebagai berikut.
![]()
Isoton adalah atom-atom yang memiliki jumlah neutron sama banyak. Jumlah neutron dari atom ![]() dapat dihitung sebagai berikut.
dapat dihitung sebagai berikut.

Jumlah neutron dari atom ![]() adalah 30.
adalah 30.
Dengan menggunakan persamaan yang sama, jumlah neutron pada opsi A sampai E adalah sebagai berikut.

Dengan demikian, isoton dari atom ![]() adalah
adalah karena memiliki jumlah neutron yang sama, yaitu 30.

13. Topik: Aljabar
Subtopik: Konsep Kilat Persamaan dan Pertidaksamaan
Perhatikan notasi atom berikut ini!
![]()
Y: lambang atom
A: nomor massa
Z: nomor atom atau jumlah proton
Isoton adalah atom-atom yang memiliki jumlah neutron sama banyak. Jumlah neutron dapat dihitung dengan menggunakan persamaan berikut.
![]()
Diketahui ![]() merupakan isoton dari atom
merupakan isoton dari atom ![]() .
.
Tentukan nilai kebenaran dari pernyataan-pernyataan berikut!
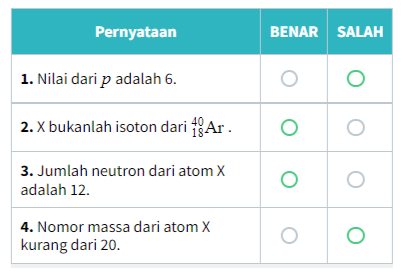
Jawaban:
Pernyataan 2 dan 3 bernilai BENAR. Sementara itu, pernyataan 1 dan 4 bernilai SALAH.
Pembahasan:
Pada soal, diketahui persamaan sebagai berikut.
![]()
Dari persamaan tersebut, didapat bahwa jumlah neutron bisa dihitung sebagai berikut.
![]()
Isoton adalah atom-atom yang memiliki jumlah neutron sama banyak. Jumlah neutron dari atom ![]() adalah sebagai berikut.
adalah sebagai berikut.
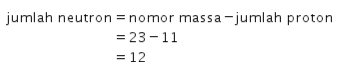
Didapat jumlah neutron dari atom ![]() adalah 12.
adalah 12.
Dengan menggunakan persamaan yang sama, jumlah neutron dari ![]() dapat dihitung sebagai berikut.
dapat dihitung sebagai berikut.
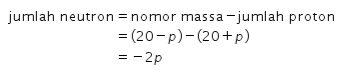
Didapat jumlah neutron dari atom ![]() adalah -2p.
adalah -2p.
Karena diketahui ![]() merupakan isoton dari atom
merupakan isoton dari atom ![]() , maka jumlah neutron dari kedua atom haruslah bernilai sama. Oleh karena itu, jumlah neutron dari
, maka jumlah neutron dari kedua atom haruslah bernilai sama. Oleh karena itu, jumlah neutron dari ![]() adalah 12.
adalah 12.
Dengan demikian, pernyataan 3 bernilai BENAR.
Karena sebelumnya didapat bahwa jumlah neutron dari atom ![]() adalah -2p, maka didapat perhitungan sebagai berikut.
adalah -2p, maka didapat perhitungan sebagai berikut.
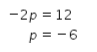
Didapat bahwa nilai dari p adalah -6.
Dengan demikian, pernyataan 1 bernilai SALAH.
Karena p=-6, didapat bahwa notasi dari atom X dapat dituliskan sebagai berikut.
![]()
Oleh karena itu, didapat bahwa nomor massa dari atom X adalah 26 dan jumlah proton dari atom X adalah 14.
Dapat diperhatikan bahwa nomor massa dari atom X lebih dari 20 sehingga pernyataan 4 bernilai SALAH.
Selanjutnya, untuk menentukan nilai kebenaran dari pernyataan 2, tentukan jumlah neutron dari ![]() terlebih dahulu sebagai berikut.
terlebih dahulu sebagai berikut.
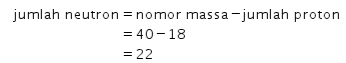
Didapat bahwa jumlah neutron dari ![]() adalah 22 sehingga berbeda dengan jumlah neutron dari X. Oleh karena itu, X bukanlah isoton dari
adalah 22 sehingga berbeda dengan jumlah neutron dari X. Oleh karena itu, X bukanlah isoton dari ![]() .
.
Dengan demikian, pernyataan 2 bernilai BENAR.

14. Topik: Bilangan
Subtopik: Konsep Kilat Operasi Hitung Bilangan
Perhatikan notasi atom berikut ini!
![]()
Y: lambang atom
A: nomor massa
Z: nomor atom atau jumlah proton
Isoton adalah atom-atom yang memiliki jumlah neutron sama banyak. Jumlah neutron dapat dihitung dengan menggunakan persamaan berikut.
![]()
Diketahui pula bahwa ion adalah atom yang memiliki muatan. Besar muatan umumnya dapat ditentukan dari notasi yang ditulis pada bagian kanan atas ion. Sebagai contoh, besar muatan dari ion ![]() secara berurutan adalah -2, -1, +1, dan +2.
secara berurutan adalah -2, -1, +1, dan +2.
Jumlah elektron dari ion dapat dihitung dengan persamaan berikut.
![]()
Jumlah proton, elektron, dan neutron dari ion ![]() secara berurutan adalah ….
secara berurutan adalah ….
- 19, 20, 18
- 20, 19, 18
- 18, 19, 39
- 19, 39, 18
- 19, 18, 20
Jawaban: E
Pembahasan:
Dari ion ![]() , diketahui nomor massanya adalah 39, nomor atom atau jumlah protonnya adalah 19, dan besar muatannya adalah +1. Jumlah elektron dari ion tersebut dapat dihitung sebagai berikut..
, diketahui nomor massanya adalah 39, nomor atom atau jumlah protonnya adalah 19, dan besar muatannya adalah +1. Jumlah elektron dari ion tersebut dapat dihitung sebagai berikut..
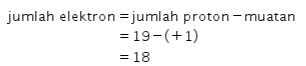
Kemudian, jumlah neutron dari ion tersebut dapat dihitung sebagai berikut.

Dengan demikian, jumlah proton, elektron, dan neutron secara berurutan adalah 19, 18, 20.

15. Topik: Aljabar
Subtopik: Konsep Kilat Aritmatika Sosial
Perhatikan informasi berikut!
Pajak Penghasilan (PPh) berdasarkan UU PPh didefinisikan sebagai pajak yang dikenakan kepada orang pribadi atau badan atas penghasilan yang diperoleh dalam tahun pajak. Untuk Penghasilan Tidak Kena Pajak (PTKP), karyawan yang memiliki status belum menikah dan tidak memiliki tanggungan adalah Rp54.000.000,00 per tahun. PPh termasuk ke dalam pajak progresif sehingga tarif pajak yang akan makin naik sesuai dengan naiknya dasar pengenaan pajak. Diketahui perhitungan tarif PPh berdasarkan pasal 21 sesuai UU PPh didasari oleh Penghasilan Kena Pajak (PKP) dan disajikan dalam tabel berikut.
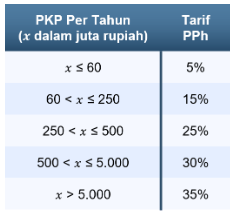
Sebagai contoh, untuk penghasilan Andi setelah dikurangi PTKP adalah Rp300.000.000,00 per tahun, maka dikenakan tarif pajak sampai lapis ketiga, yaitu 25%. Pada tarif lapis pertama, Rp60.000.000,00 pertama dikenakan tarif pajak 5%. Kemudian, pada tarif lapis kedua, Rp190.000.000,00 berikutnya (dari 60 juta sampai 250 juta) dikenakan tarif pajak 15%. Selanjutnya, pada tarif lapis terakhir, sisa Rp50.000,000 dikenakan tarif pajak 25%.
Diketahui Egi adalah seorang karyawan tetap PT X dengan status belum menikah dan tidak memiliki tanggungan dengan penghasilan netto sebesar Rp 16.000.000,00 per bulan. Tarif pajak tahunan yang harus dibayarkan Egi adalah ….
- Rp6.900.000,00
- Rp9.600.0000,00
- Rp11.700.000,00
- Rp14.700.000,00
- Rp20.700.000,00
Jawaban: D
Pembahasan:
Perhatikan bahwa penghasilan netto Egi sebesar Rp16.000.000,00 per bulan sehingga penghasilan Egi dalam setahun adalah sebagai berikut.
![]()
Karena Egi belum menikah dan tidak memiliki tanggungan, maka PTKPnya adalah Rp54.000.000,00 sehingga penghasilan kena pajaknya adalah sebagai berikut.
![]()
Karena Penghasilan Kena Pajak (PKP) Egi lebih dari Rp60.000.000,00 dan kurang dari Rp250.000.000,00, maka Egi dikenakan tarif pajak progresif hingga tarif lapis kedua, yaitu 15%.
Untuk menghitung pajak penghasilannya, maka dibagi menjadi dua lapis tarif, yaitu lapis pertama (5%) dan sisa perhitungan lainnya dihitung dengan tarif lapisan kedua (15%) dengan perhitungan sebagai berikut.
Lapisan pertama: dikenakan tarif 5%.
![]()
Lapisan kedua: dikenakan tarif 15%.
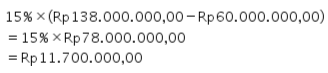
Oleh karena itu, Pajak Penghasilan Egi secara progresif adalah sebagai berikut.
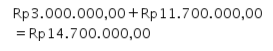
Dengan demikian, Pajak Penghasilan Egi secara progresif adalah Rp14.700.000,00 per tahun.

16. Topik: Aljabar
Subtopik: Konsep Kilat Aritmatika Sosial
Perhatikan informasi berikut!
Pajak Penghasilan (PPh) berdasarkan UU PPh didefinisikan sebagai pajak yang dikenakan kepada orang pribadi atau badan atas penghasilan yang diperoleh dalam tahun pajak. Untuk Penghasilan Tidak Kena Pajak (PTKP), karyawan yang memiliki status belum menikah dan tidak memiliki tanggungan adalah Rp54.000.000,00 per tahun. PPh termasuk ke dalam pajak progresif sehingga tarif pajak yang akan makin naik sesuai dengan naiknya dasar pengenaan pajak. Diketahui perhitungan tarif PPh berdasarkan pasal 21 sesuai UU PPh didasari oleh Penghasilan Kena Pajak (PKP) dan disajikan dalam tabel berikut.

Sebagai contoh, untuk penghasilan Andi setelah dikurangi PTKP adalah Rp300.000.000,00 per tahun, maka dikenakan tarif pajak sampai lapis ketiga, yaitu 25%. Pada tarif lapis pertama, Rp60.000.000,00 pertama dikenakan tarif pajak 5%. Kemudian, pada tarif lapis kedua, Rp190.000.000,00 berikutnya (dari 60 juta sampai 250 juta) dikenakan tarif pajak 15%. Selanjutnya, pada tarif lapis terakhir, sisa Rp50.000,000 dikenakan tarif pajak 25%.
John adalah seorang guru dengan status belum menikah dan tidak memiliki tanggungan dengan penghasilan netto sebesar Rp4.000.000,00 per bulan. Tarif pajak tahunan yang harus dibayar oleh John adalah ….
- Rp0,00
- Rp200.000,00
- Rp300.000,00
- Rp2.400.000,00
- Rp2.700.000,00
Jawaban: A
Pembahasan:
Misalkan penghasilan John selama 1 tahun adalah P, maka besarnya dalam setahun adalah sebagai berikut.
![]()
Karena Penghasilan Tidak Kena Pajak (PTKP) karyawan yang memiliki status belum menikah dan tidak memiliki tanggungan adalah Rp54.000.000,00 per tahun dan penghasilan John selama 1 tahun hanya Rp48.000.000,00, maka John tidak berkewajiban membayar pajak.
Dengan demikian, tarif pajak tahunan yang harus dibayar oleh John adalah Rp0,00.

17. Topik: Pengukuran dan Geometri
Subtopik: Konsep Kilat Bangun Datar
Perhatikan ilustrasi berikut!
Tujuh buah silinder dengan jari-jari 7 cm disusun dan dibungkus sehingga membentuk tampak atas seperti gambar berikut.
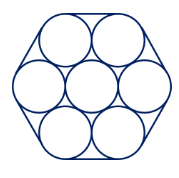
Jika ketujuh silinder tersebut dililit beberapa lapis oleh tali yang panjangnya 768 cm, banyak lilitan yang dibuat adalah … lapis.
Catatan: Gunakan ![]()
- 2
- 3
- 4
- 6
- 9
Jawaban: D
Pembahasan:
Gambar pada soal dapat dibuat garis bantu seperti gambar berikut.
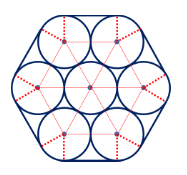
Dari gambar, dapat disimpulkan bahwa lilitan terbentuk dari komponen-komponen berikut.
- Enam buah garis lurus yang panjangnya adalah 2r.
- Enam buah busur lingkaran yang membentuk keliling 1 lingkaran.
Keliling satu lilitan dapat dihitung dengan persamaan berikut.
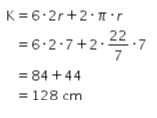
Kemudian, ketujuh silinder tersebut dililit beberapa lapis oleh tali yang panjangnya 768 cm.
Oleh karena itu, banyak lilitan yang dibuat adalah ![]()

18. Topik: Pengukuran dan Geometri
Subtopik: Konsep Kilat Bangun Ruang
Perhatikan ilustrasi berikut!
Tujuh buah silinder dengan jari-jari 7 cm disusun dan dibungkus sehingga membentuk tampak atas seperti gambar berikut.

Jika luas selimut bangun ruang yang dimaksud sebesar ![]() , tinggi masing-masing tabung adalah sebesar … cm.
, tinggi masing-masing tabung adalah sebesar … cm.
Catatan: Gunakan ![]()
- 6,9
- 7
- 9,1
- 5
- 5,5
Jawaban: E
Pembahasan:
Luas selimut bangun ruang sisi lengkung melibatkan keliling alas dan tinggi bangun ruang. Gambar pada soal dapat dibuat garis bantu seperti gambar berikut untuk menentukan keliling alasnya.

Dari gambar, dapat disimpulkan bahwa keliling alas terbentuk dari komponen-komponen berikut.
- Enam buah garis lurus yang panjangnya adalah 2r.
- Enam buah busur lingkaran yang membentuk keliling 1 lingkaran.
Keliling alas dapat dihitung dengan persamaan berikut.
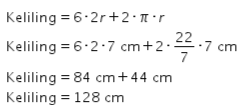
Luas selimut bangun ruang mengikuti persamaan matematis berikut.


19. Topik: Data dan Ketidakpastian
Subtopik: Konsep Kilat Statistika Deskriptif
Perhatikan informasi berikut!
Berdasarkan perspektif ekonomi, usia penduduk dikategorikan menjadi dua bagian, yaitu usia produktif (15—59 tahun) dan usia tidak produktif (di bawah 15 tahun dan 60 tahun ke atas). Jumlah penduduk pada suatu negara tahun 2021 tercatat sebagai berikut.
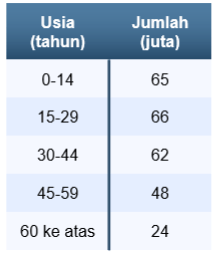
Jika dipilih satu orang dari negara tersebut pada tahun 2021, peluang terpilihnya seseorang yang berada pada usia produktif setelah dilakukan pembulatan adalah sekitar ….
- 0,66
- 0,67
- 0,72
- 0,75
- 0,90
Jawaban: A
Pembahasan:
Peluang terpilihnya seseorang yang berada pada usia produktif dapat dihitung sebagai berikut

Dengan demikian, peluang terpilihnya seseorang yang berada pada usia produktif adalah sekitar 0,66.

20. Topik: Data dan Ketidakpastian
Subtopik: Konsep Kilat Statistika Deskriptif
Perhatikan informasi berikut!
Berdasarkan perspektif ekonomi, usia penduduk dikategorikan menjadi dua bagian, yaitu usia produktif (15—59 tahun) dan usia tidak produktif (di bawah 15 tahun dan 60 tahun ke atas). Jumlah penduduk pada suatu negara tahun 2021 tercatat sebagai berikut.

Persentase penduduk yang berusia 30—44 tahun terhadap jumlah seluruh penduduk yang berada pada usia produktif adalah sekitar ….
- 37,50%
- 35,23%
- 31,52%
- 27,28%
- 24,22%
Jawaban: B
Pembahasan:
Kategori penduduk usia 30—44 tahun atau dapat ditulis n(30-44) merupakan kategori usia produktif dengan jumlah penduduk sebesar 62 juta jiwa.
Sementara itu, penduduk yang berada pada usia produktif merupakan penduduk dengan kelompok usia 15—59 tahun dengan jumlah penduduk sebagai berikut.
![]()
Persentase penduduk yang berusia 30—44 tahun terhadap jumlah seluruh penduduk yang berada pada usia produktif dapat dihitung sebagai berikut.
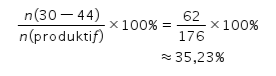
Dengan demikian, persentase penduduk yang dimaksud adalah sekitar 35,23%.

21. Topik: Bedah Contoh Soal Penalaran Matematika
Subtopik: Pengukuran dan Geometri
Level Kognitif: HOTS
Perhatikan ilustrasi berikut!
Joni sedang menyusun strategi olahraga yang bertujuan untuk menurunkan berat badan. Dia berencana akan melakukan joging di sebuah lapangan yang berbentuk
persegi panjang dan berukuran 90 m × 60 m. Diketahui bahwa jumlah kalori yang terbakar ketika ia melakukan joging dengan kecepatan konstan sebesar 2m/s selama 30 menit adalah sekitar 200 kalori. Jika dalam 30 hari total kalori minimal yang ingin ia bakar melalui joging dengan kecepatan 2m/s adalah 10.000 kalori, rencana joging berikut yang mendekati target Joni adalah ….
Catatan: Jawaban bisa lebih dari satu
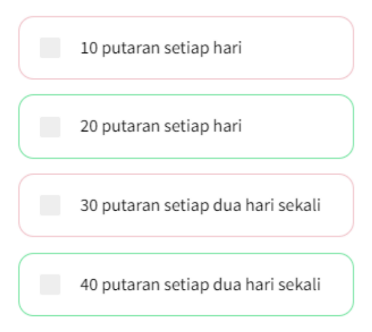
Jawaban: yang dikotak hijau
Pembahasan:
Diketahui kalori yang terbakar saat joging dengan kecepatan 2m/s selama 30 menit adalah 200 kalori dan target yang ingin dicapai minimal adalah 10.000 kalori dalam 30 hari.
Hitung keliling lapangan tersebut untuk mengetahui jarak yang telah ditempuh Joni saat joging melakukan 1 putaran.
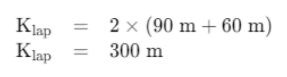
Hitung lama waktu joging yang dibutuhkan untuk membakar 10.000 kalori.

Hitung jarak yang dapat ditempuh ketika melakukan joging dengan kecepatan 2m/s selama 1.500 menit.

Hitung jumlah Joni harus memutari lapangan untuk mencapai jarak 180.000 m.

Karena sudah diketahui berapa kali Joni harus memutari lapangan tersebut untuk membakar minimal 10.000 kalori dalam 30 hari, maka perlu dihitung jumlah putaran dari masing-masing pernyataan.
- Pernyataan 1 = 10 putaran setiap hari. Artinya, selama 30 hari Joni akan lari sebanyak 30 kali. Oleh karena itu, jumlah putaran dalam 30 hari adalah 10 putaran × 30 = 300 putaran. Dengan demikian, pernyataan ini bernilai SALAH.
- Pernyataan 2 = 20 putaran setiap hari. Artinya, selama 30 hari Joni akan lari sebanyak 30 kali. Oleh karena itu, jumlah putaran dalam 30 hari adalah 20 putaran × 30 = 600 putaran. Dengan demikian, pernyataan ini bernilai BENAR.
- Pernyataan 3 = 30 putaran setiap dua hari sekali. Artinya, selama 30 hari Joni akan lari sebanyak 15 kali. Oleh karena itu, jumlah putaran dalam 30 hari adalah 30 putaran × 15 = 450 putaran. Dengan demikian, pernyataan ini bernilai SALAH.
- Pernyataan 4 = 40 putaran setiap dua hari sekali. Artinya, selama 30 hari Joni akan lari sebanyak 15 kali. Oleh karena itu, jumlah putaran dalam 30 hari adalah 40 putaran × 15 = 600 putaran. Dengan demikian, pernyataan ini bernilai BENAR.
Jadi, Joni harus melakukan joging 20 putaran setiap hari atau 40 putaran setiap dua hari sekali untuk mencapai target membakar 10.000 kalori melalui joging selama 30 hari.

Contoh Soal Isian
22. Topik: Bedah Contoh Soal Penalaran Matematika
Subtopik: Aljabar
Level Kognitif: HOTS
Perhatikan teks berikut!
Yoga memiliki wadah-wadah dengan tiga ukuran yang berbeda, yaitu S, M, dan L. Diketahui massa wadah berukuran M adalah dua kali lipat massa wadah berukuran S dan setiap wadah dengan ukuran yang sama memiliki massa yang sama. Ia kemudian menimbang kombinasi dua wadah dari wadah-wadah yang dimilikinya pada timbangan digital dan didapat hasil sebagai berikut.
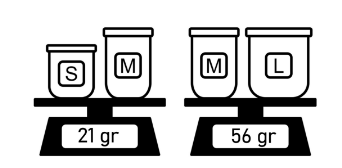
Jika Yoga menimbang 2 wadah berukuran L bersama-sama, massa kedua wadah tersebut adalah … gram.
Catatan: Hanya diisi dengan angka (contoh: 10)
Jawaban: 84
Pembahasan:
Misalkan x, y, dan z secara berurutan menyatakan massa wadah S, M, dan L. Berdasarkan gambar pada soal, didapat persamaan-persamaan sebagai berikut.
x + y = 21
y + z = 56

Diperoleh z = 42, dengan kata lain massa dari wadah berukuran L adalah 42 gram. Oleh karena itu, jika dua wadah berukuran L ditimbang bersama-sama, massa kedua wadah tersebut adalah 84 gram.
Jadi, jawaban yang tepat adalah 84.

Tips Mengerjakan Soal Penalaran Matematika
Gimana sih tips jitu dan cepat dalam mengerjakan soal Penalaran Matematika di UTBK-SNBT 2025 nanti? Nah, berikut beberapa cara yang bisa kamu gunakan:
- Cari tahu bentuk soal atau kisi-kisi materi yang akan diujikan nanti.
- Mengetahui konsep Matematika Dasar.
- Fokus pada konteks masalah yang dipertanyakan pada soal.
- Mengira-ngira estimasi waktu pengerjaan.
- Jangan terjebak pada soal yang sulit.
Mudah dipahami kan, guys? Nggak perlu takut atau panik, dengan banyak berlatih contoh soal Penalaran Matematika UTBK-SNBT pasti kamu bisa lebih mudah untuk mengerjakannya di hari ujian nanti. Yuk, latihan lebih banyak soal dan uji kemampuan kamu dengan ikutan tryout UTBK SNBT di ruanguji.
















