Pengertian Bilangan Prima, Contoh, dan Cara Mencarinya

Ternyata bilangan prima berperan dalam menjaga akun sosial media kamu agar tidak ‘dibajak’ oleh orang lain. Bilangan prima digunakan dalam pesan enkripsi untuk menjaga keamanan kata sandi elektronik, mulai dari PIN ATM, password, akun sosial media, e-mail, dan lainnya.

—

Pastinya kamu sudah tidak asing dengan istilah ‘bilangan prima’, bukan? Yup, bilangan prima sudah diajarkan sejak kita menginjak sekolah dasar. Tapi apa sih sebenarnya bilangan prima itu? Apa fungsinya? Kenapa harus ada bilangan prima? Yuk, kita bahas di sini!

Pengertian Bilangan Prima

Apa itu bilangan prima? Bilangan prima adalah sebuah bilangan asli lebih dari 1, yang hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri. Sederhananya, bilangan prima adalah bilangan yang hanya bisa dibagi 1 dan bilangan itu sendiri.

Apakah bilangan ganjil juga termasuk bilangan prima? Jawabannya tidak! Karena ada bilangan ganjil yang bisa dibagi oleh bilangan lain, selain 1 dan bilangan itu sendiri. Contohnya angka 9 yang bukan bilangan prima. Sebab, 9 bisa dibagi 1, 9, dan 3.

Nah, contoh 10 bilangan prima pertama adalah 2, 3, 5, 7, 11, 13, 17, 19, 23, dan 29.

Euclid (Britannica.com)

Sejarah Bilangan Prima

Nah, sejarah bilangan prima pertama kali ditemukan pada sebuah catatan berumur 300 tahun Sebelum Masehi (SM), milik Euclid seorang matematikawan asal Alexandria. Dia menjelaskan bahwa jumlah bilangan prima itu tidak terbatas. 

Eratosthenes (www.thoughtco.com)

Berikutnya, pada tahun 200 SM, ilmuwan matematika asal Kirene bernama Eratosthenes, berusaha membuat saringan Eratosthenes untuk mencari bilangan prima. Cara tersebut digunakan untuk memisahkan bilangan bukan prima (bilangan komposit) pada rentang bilangan tertentu untuk menemukan bilangan prima.

Baca Juga: Sejarah Sandi Morse, Rumus, dan Cara Menghafalnya dengan Mudah

Contoh Bilangan Prima antara 1-100

Pasti sekarang banyak di antara kamu yang penasaran kan, apa saja angka yang termasuk bilangan prima antara 1-100. Total ada 25 bilangan prima antara 1-100. Apa aja tuh? Berikut adalah daftar lengkap bilangan prima antara 1 sampai 100:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, dan 97.

Cara Menentukan Bilangan Prima

Setelah mengetahui definisi dan sejarahnya, sekarang coba kita cari tahu gimana cara menentukan bilangan prima. Yuk, kita coba saringan Eratosthenes ini!

Pertama, kita buat kotak sesuai dengan jumlah angka yang akan kita cari bilangan primanya. Di sini, kita ingin mengetahui berapa banyak bilangan prima 1 sampai 30. Oleh karena itu, kita buat 30 kotak dan isi setiap kotak dengan angka 1 sampai 30. 

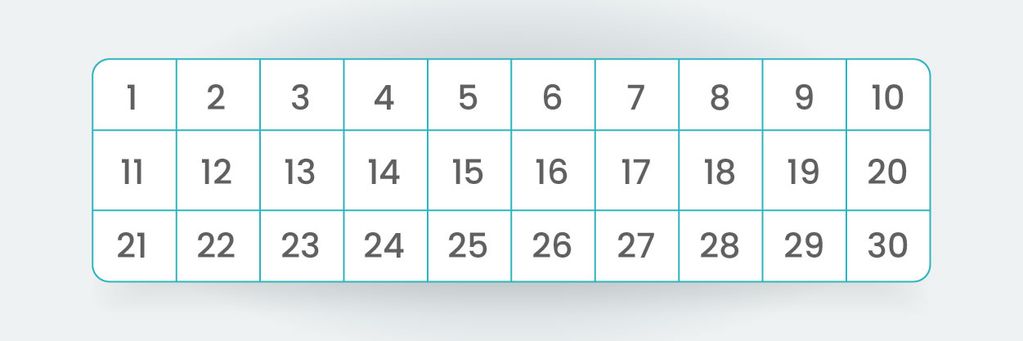
Berikutnya, kita abaikan angka 1 ya guys, karena jelas angka 1 bukan bilangan prima. Kita langsung menuju angka 2. Nah, di sini kita akan memisahkan bilangan komposit dengan bilangan prima.

Jadi, yang perlu kita lakukan adalah mencari setiap kelipatan dari bilangan prima yang kita temui di awal. Angka 2 kita tandai warna hijau sebagai bilangan prima, lalu untuk kelipatannya, kita tandai warna merah sebagai tanda bukan bilangan prima.

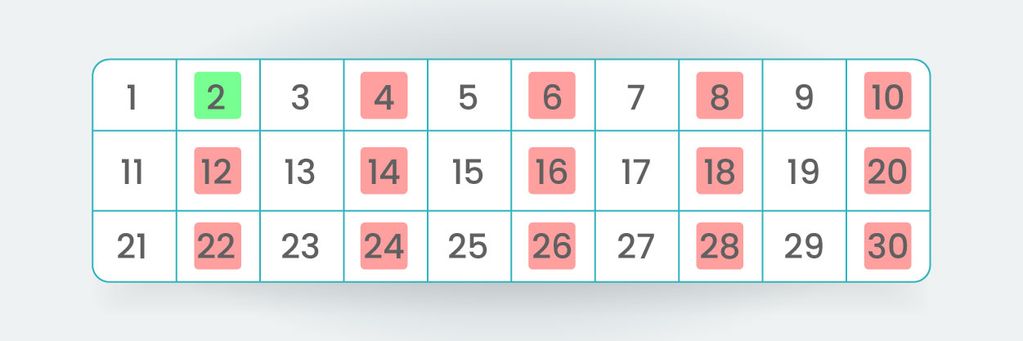
Sekarang, kita lanjut ke angka berikutnya, yaitu angka 3. Angka 3 dan angka-angka selanjutnya yang belum berwarna merah, berarti bukan merupakan kelipatan 2. Artinya, angka-angka ini memiliki kemungkinan termasuk ke dalam bilangan prima.

Nah, kita tandai hijau pada angka 3 sebagai bilangan prima, lalu cari kelipatan 3 dan tandai dengan warna merah sebagai bilangan bukan prima.

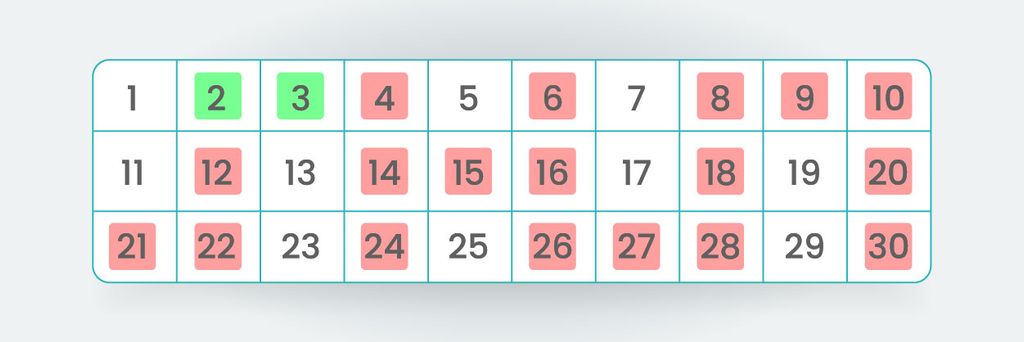
Lalu, berikutnya setelah angka 3 adalah angka 4, tapi 4 sudah ditandai merah, jadi kita lanjut ke angka berikutnya, yaitu 5. Kita tandai 5 sebagai bilangan prima, lalu tandai kelipatannya sebagai bilangan bukan prima.

Lakukan secara terus menerus langkah seperti di atas sampai semua angka benar-benar selesai ditandai. Hasilnya akan menjadi seperti berikut:

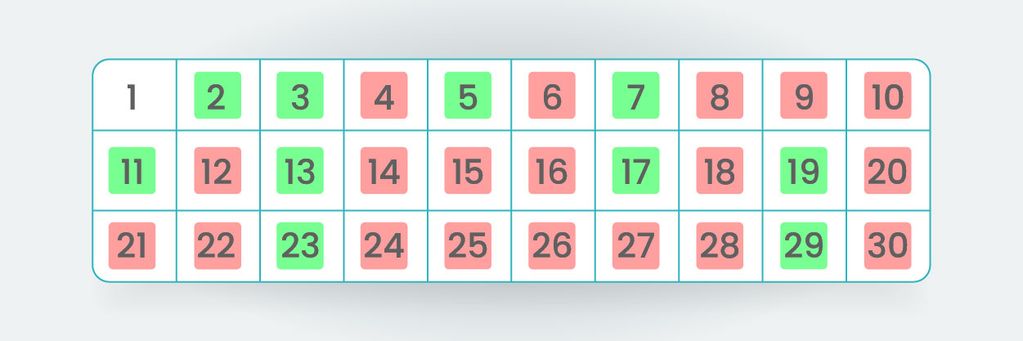
Jadi, dari angka 1 sampai 30, bilangan prima yang didapat adalah 2, 3, 5, 7, 11, 13, 17, 19, 23, dan 29. Cukup mudah, bukan? Kamu bisa mencoba sampai jumlah angka yang lebih besar. Tetapi cara ini memakan waktu cukup banyak dan tidak efisien.

Gambar: Marin Mersenne (Researchgate.net)

Rumus Bilangan Prima

Perkembangan bilangan prima kemudian berlanjut pada abad ke-17, di mana seorang Biarawan Prancis bernama Marin Mersenne, menemukan sebuah rumus untuk mencari bilangan prima.

Rumus bilangan prima Mersenne adalah, Mn = (2^n) – 1. Di mana n adalah bilangan prima dan Mn adalah bilangan prima yang baru didapatkan.

Jadi, jika 2 dipangkatkan oleh sebuah bilangan prima dan dikurang satu, maka akan menghasilkan bilangan prima. contohnya n = 3, maka rumusnya menjadi (2^3) – 1 = 7, dan 7 merupakan bilangan prima.

Baca Juga: Point Nemo, Lokasi Paling Jauh di Bumi yang Jadi Kuburan Pesawat Luar Angkasa

Tetapi rumus Mersenne ini memiliki keterbatasan, karena beberapa hasilnya menunjukan bilangan bukan prima, seperti pada n = 11 dan n = 67. Oleh karena itu, pencarian lewat rumus ini harus dibarengi dengan pengujian atau verifikasi lebih lanjut. 

Berkat rumus Mersenne, telah ditemukan bilangan prima terbesar sampai saat ini. Tepatnya pada tahun 2018 dalam sebuah proyek bernama GIMPS atau disebut Great Internet Mersenne Prime Search oleh Patrick Laroche. Rumusan angkanya adalah 2^82589933 – 1 yang jika dijabarkan, total digit angkanya bisa mencapai 24,862,048. 

Fungsi Bilangan Prima

Apa sih fungsi bilangan prima dalam kehidupan sehari-hari kita? Ada dua fungsi utama dari bilangan prima yang akan kita bahas. Simak penjelasannya ya.

1. Mencari KPK dan FPB

Bilangan prima ini adalah bilangan utama pembentuk bilangan bulat, jadi semua bilangan bulat bisa dibentuk dari bilangan prima. Lewat bilangan prima, kita bisa menentukan pohon faktor dari sebuah bilangan untuk menentukan faktorisasi primanya.

Bagaimana cara mencari faktorisasi prima lewat pohon faktor? Pertama, tuliskan angka yang akan dicari faktorisasi primanya. Kemudian, bagi bilangan tersebut mulai dari bilangan prima terkecil lebih dahulu, yaitu 2 sampai bilangan tersebut tidak bisa dibagi lagi, selain dengan 1 dan dirinya sendiri.

   16

    / 

 2     8

         /

      2     4

             /

          2     2

16 = 2⁴

Nah, lewat cara ini, kita juga bisa dengan mudah mencari kelipatan persekutuan terkecil (KPK) dan faktor persekutuan terbesar (FPB). Contohnya dalam mencari KPK dalam persoalan berikut:  

Santi akan libur setelah 4 hari bekerja, sedangkan Yuni akan libur setelah 6 hari bekerja, kapan mereka akan liburan secara bersama? Pertama, kita tentukan dulu faktorisasi prima dari 4 dan 6:

    4

   /

 2   2

    6

    /

 2    3

Faktorisasi Primanya:

4 = 2²  

6 = 2 x 3

Berikutnya, dalam mencari KPK, kalikan semua faktor prima dari kedua angka. Tapi, jika ditemukan faktor yang sama, pilihlah faktor dengan pangkat yang paling besar nilainya.

Dari 4 dan 6, ada faktor yang sama, yaitu 2. Kita pilih faktor dengan pangkat terbesar, yaitu 2². Sehingga, KPK: 2² x 3 = 12, maka Yuni dan Santi akan libur bersama setelah 12 hari bekerja.

Nah, untuk FPB bisa berguna untuk mencari sebuah komposisi atau pecahan yang seimbang. Contohnya Dirman, seorang koki memiliki 6 kepiting, 9 udang, dan 15 ikan. Dia ingin membuat menu seimbang di mana ketiga bahan tersebut masuk ke dalam setiap porsi. Berapa porsi masakan yang bisa Dirman buat dengan kandungan bahan yang seimbang? 

Tentukan terlebih dahulu faktorisasi prima dari ketiga bilangan tersebut.

    6

    /

 2    3

     9

    /

  3   3

   15

    /

 3    5

Faktorisasi Prima:

6 = 2 x 3 

9 = 3² 

15 = 3 x 5 

Untuk mencari FPB, pilih faktor prima yang sama, kemudian pilih yang terkecil nilai pangkatnya, lalu kalikan. Karena pada 6, 9, dan 15, faktor prima yang sama hanya 1 faktor, yaitu 3, maka kita pilih faktor dengan pangkat terkecil, yaitu 3.

Jadi, FPB dari 6, 9, dan 15 adalah 3. Sehingga, Dirman hanya bisa membuat 3 porsi makanan dengan kandungan 2 kepiting, 3 udang, dan 5 ikan pada setiap porsinya.

Baca Juga: Pernah Alami Brain Freeze? Ini yang Sebenarnya Terjadi pada Tubuh Kita

2. Alat Keamanan dalam Menyimpan Password

Selanjutnya, ada satu lagi nih fungsi bilangan prima yang cukup berguna bagi kita, yaitu sebagai alat keamanan untuk menyimpan password dan pesan rahasia. Lho, kok bisa? Jadi, bilangan prima ini digunakan dalam kriptografi, atau teknik penyampaian pesan rahasia.

Pesan rahasia yang kamu sering tulis akan diubah atau dienkripsi ke dalam sebuah angka untuk menghindari peretasan. Nah angka tersebut adalah hasil dari perkalian 2 buah bilangan prima.

Pesan tersebut baru akan bisa terbaca saat sistem mengetahui 2 faktor bilangan prima yang sudah dikalikan tersebut. Alhasil, perkalian 2 bilangan prima ini menjadi cara untuk mengamankan banyak password, pesan rahasia, PIN ATM, dan informasi elektronik lainnya.

Jadi, walau sebuah informasi bocor, tentunya akan sangat sulit menerjemahkan bilangan tersebut menjadi sebuah pesan. 

Kok bisa begitu? Karena secara logika, akan membutuhkan waktu yang sangat lama untuk mencari faktor prima dari sebuah bilangan yang cukup besar. Biasanya enkripsi modern menggunakan bilangan dengan ratusan digit angka dan butuh waktu ratusan tahun untuk bisa mencari faktor prima dari bilangan tersebut.

—

Jadi, bilangan prima ini merupakan bilangan inti yang membangun semua bilangan bulat, karena semua bilangan bulat bisa dibentuk dari sebuah faktor prima. Bilangan prima akan semakin jarang ditemukan seiring bertambahnya angka.

Walau begitu, bilangan prima yang unik ini banyak membantu manusia untuk memecahkan masalah perhitungan seperti mencari momentum, mencari keseimbangan komposisi, dan mengamankan sebuah jaringan. 

Ingin mengetahui banyak hal tentang matematika, khususnya bilangan prima? Tenang, matematika tidak selalu membosankan kok. Cobain yuk, salah satu aplikasi belajar yang asik banget, yaitu ruangbelajar. Dapatkan pengalaman menarik belajar matematika tanpa perlu takut pusing bersama master teacher terbaik.

Referensi:

Firmansyah, Faurizal Fahmi (2014) “Kajian matematis dan penggunaan bilangan prima pada algoritma kriptografi RSA (Rivest, Shamir, dan Adleman) dan algoritma kriptografi Elgamal” [online]. Undergraduate thesis, Universitas Islam Negeri Maulana Malik Ibrahim. (diakses 20 November 2021)

Gregersen, Erik. “Prime Numbers”. Encyclopedia Britannica, https://www.britannica.com/story/prime-numbers (diakses 20 November 2021) 

Hosch, William L.. “Mersenne prime”. Encyclopedia Britannica, 19 September 2019, https://www.britannica.com/science/Mersenne-prime  (diakses 23 November 2021)

Britannica, The Editors of Encyclopaedia. “sieve of Eratosthenes”. Encyclopedia Britannica, 8 Oktober 2013, https://www.britannica.com/science/sieve-of-Eratosthenes. (diakses 23 November 2021)

Sumber Foto:

Shirali, Shailesh. (2013). Marin Mersenne, 1588–1648. https://www.researchgate.net/figure/Father-Marin-Mersenne-in-his-cell_fig1_257768125 (diakses 20 November 2021)

Science History Images/Alamy. Euclid. https://www.britannica.com/biography/Euclid-Greek-mathematician (diakses 20 November 2021)

Heritage Images / Getty Images. Erathsthenes. https://www.thoughtco.com/eratosthenes-biography-1435011 (diakses 20 November 2021)

Artikel ini terakhir diperbarui pada 1 Mei 2024.