Optimasi dan Program Linear | Matematika Kelas 11

Cara menyelesaikan program linear dengan mudah dibahas di artikel ini melalui contoh nyata di kehidupan sehari-hari dan lingkungan sekitar.

—

Siapa sih yang nggak mengagumi Bapak Proklamasi kita, Ir. Soekarno? Jasanya buesaaaar sekali bagi kemerdekaan Indonesia, Squad. Namun tahu nggak kalau ia pernah punya sahabat? Yap, namanya adalah Che Guevara, revolusioner sekaligus Menteri Perindustrian negara Kuba. Bayangin, sama gigihnya seperti Bung Karno, Che Guevara mengangkat perekonomian Kuba dari keadaan genting memakai prinsip penyelesaian program linear dalam matematika!

Fyi, penyelesaian program linear dipakai untuk optimasi atau mencari nilai yang paling efektif dari suatu proses. Nah, Che Guevara memanfaatkannya untuk mengolah industri-industri Kuba. Program linear membantu mengetahui berapa sih bahan baku yang harus dipakai suatu pabrik agar biaya produksi serendah mungkin tapi keuntungannya semaksimal mungkin. Penasaran kan gimana cara optimasi dengan menyelesaikan program linear? Cekidot!

Presiden Soekarno berdiskusi dengan Che Guevara (sumber: liputan6.com)

Program linear biasanya berbentuk sistem pertidaksamaan linear dua variabel, Squad. Kamu harus mengingat kembali materi pertidaksamaan dan sistem pertidaksamaan linear dua variabel. Perlu kamu ketahui juga kalau optimasi dengan menyelesaikan program linear ada beberapa cara. Pastinya yang diterangkan di sini yang paling mudah dong. Yuk langsung cek langkah-langkah optimasi dengan menyelesaikan program linear.

Industri yang berkembang di Kuba saat itu adalah industri gula. Misalnya untuk membuat gula pada suatu pabrik diperlukan bahan baku tebu jenis X dan Y. Banyaknya tebu X dan tebu Y yang bisa diolah tidak lebih dari 6 peti kemas. Satu peti kemas untuk tebu X beratnya 2 ton dan satu peti kemas untuk tebu Y beratnya 3 ton.

Padahal, berat total peti kemas tebu X dan Y tidak boleh lebih dari 15 ton agar kendaraan pengangkut tidak overweight. Bila satu peti kemas tebu jenis X menghasilkan 3 ton gula dan satu peti kemas tebu jenis Y menghasilkan 4 ton gula, dengan semua syarat di atas, berapa maksimum berat gula yang dapat dihasilkan?

Masalah di atas adalah masalah yang bisa diselesaikan dengan optimasi dari menyelesaikan program linear, Squad. Kok bisa? Karena kita mencari banyaknya tebu X dan Y paling efektif untuk menghasilkan gula semaksimal mungkin walaupun terdapat seperti jumlah peti kemas tidak boleh lebih dari 6 dan berat totalnya tidak boleh lebih dari 15 ton. Langsung aja yuk kita ikuti langkah-langkah di atas.

1. Buat sistem pertidaksamaan linear dari masalah yang ada

Gimana tuh cara membuat sistem pertidaksamaannya? Slow Squad mudah kok. Coba lihat nih. 

Caranya gimana hayo? Kita harus menggabungkan semua pertidaksamaan tersebut dalam satu grafik Squad. Ingat lho cara menggambar grafik yaitu cari dulu titik x saat y = 0 dan titik y saat x = 0 lalu kedua titik tersebut dihubungkan deh. Buka lagi deh materi persamaan garis lurus dan masalah polusi udara. Jangan lupa buat diarsir sesuai tanda pertidaksamaannya ya. Kalau lebih dari di atas dan kurang dari di bawah. Nanti jadi seperti ini deh.

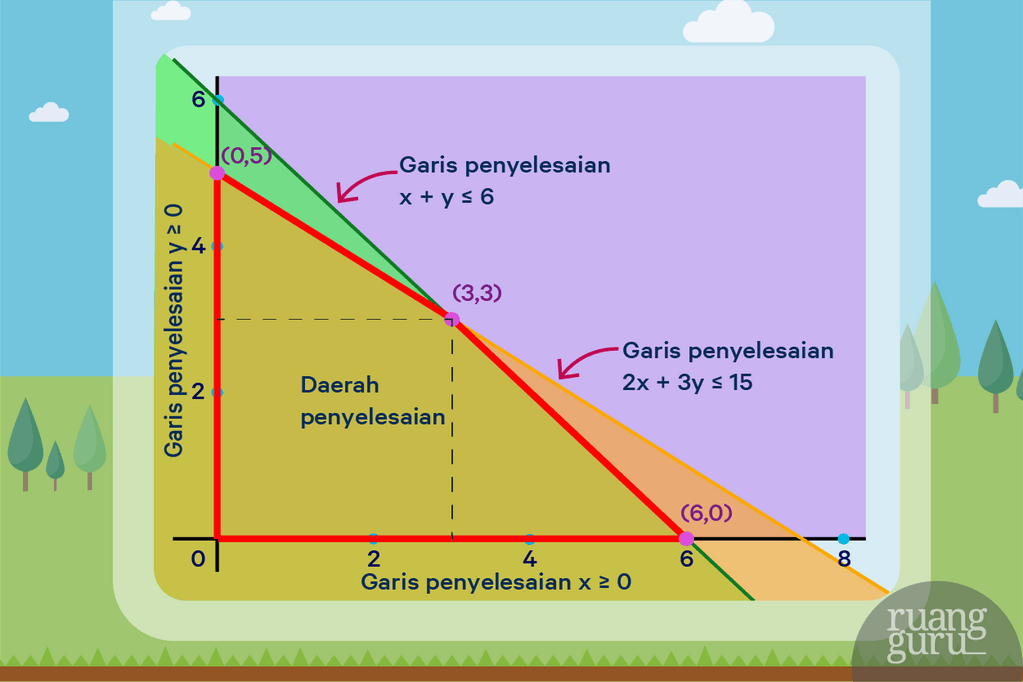
Uji titik itu gimana sih? Gini, kita kan mau tau nih jumlah gula maksimum yang dihasilkan berapa. Satu peti kemas tebu X menghasilkan 3 ton gula. Padahal ada sebanyak x peti. Maka tebu X bisa menghasilkan 3x ton gula. Begitu pula dengan tebu Y. Ada sebanyak y peti dan masing-masing menghasilkan 4 ton gula. Maka tebu Y bisa menghasilkan 4y ton gula. Maka dihasilkan total gula sebanyak

Total gula = 3x + 4y

Nah, x dan y nya diisi berapa tuh? Kita isi dengan x dan y dari titik-titik kritis. Titik kritis adalah titik yang termasuk daerah penyelesaian sistem pertidaksamaan namun merupakan titik perpotongan 2 garis atau lebih. Coba deh cari dulu titik kritisnya.

Didapat deh 3 titik kritis tuh yaitu (0,5), (3,3), dan (6,0). Langsung aja masukin semuanya ke 3x + 4y

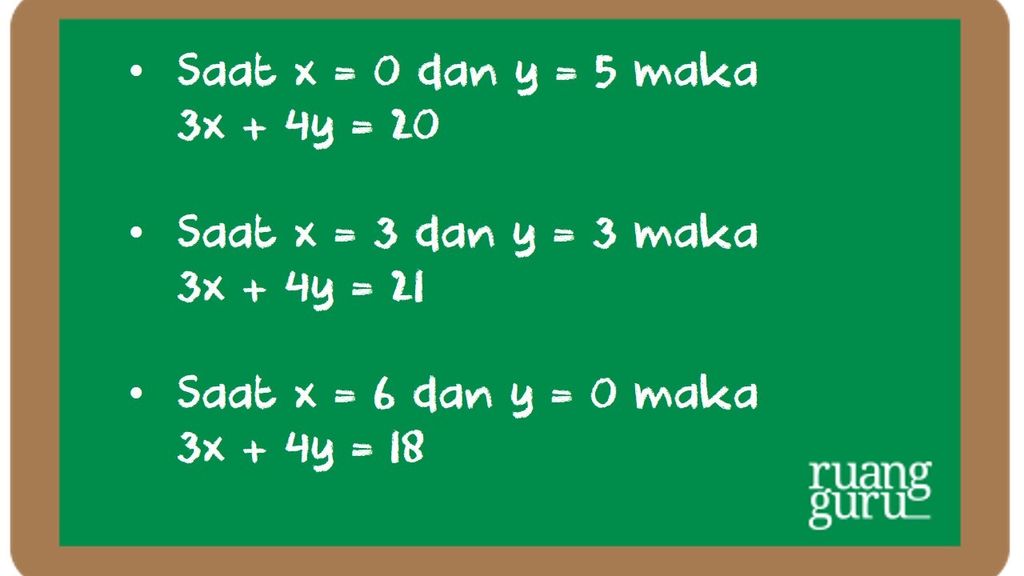
Lihat coba tuh. Saat dimasukkan x = 3 dan y = 3 maka 3x + 4y paling besar kan? Jadi agar berat gula yang dihasilkan maksimu, jumlah peti tebu jenis X haruslah sebanyak 3 peti kemas dan jenis Y haruslah sebanyak 3 peti kemas. Nanti dihasilkan deh gula seberat 21 ton.

Itu lah manfaat dari program linear. Kita bisa tahu harus berapa banyak bahan baku yang dipakai agar hasilnya bisa optimal. Kalau hasilnya optimal, untungnya gede juga dong. Pantas saja tuh Che Guevara bisa mengangkat perekonomian Kuba di zaman itu. Kalau kamu belajar yang rajin, kamu juga pasti bisa seperti dia Squad. Semangat 45!

Kalau kamu tertarik untuk belajar lebih dalam lagi, langsung aja daftar di ruangbelajar. Banyak banget lho video materi dan pembahasan soal. Tunggu apa lagi? Sikat Squad!

Sumber Referensi:

Wirodikromo, S. dan Darmanto, M. (2019) Matematika untuk SMA/MA Kelas XI kelompok Wajib 2. Jakarta:Erlangga

Referensi Gambar:

Foto ‘Presiden Soekarno berdiskusi dengan Che Guevara’ [Daring]. Tautan:https://m.liputan6.com/news/read/2217098/kisah-persahabatan-bung-karno-dan-che-guevara-usai-kaa-1955 (Diakses: 14 Desember 2020)

Artikel diperbaharui 14 Desember 2020