Cara Menyelesaikan Operasi Perpangkatan pada Bentuk Aljabar | Matematika Kelas 7

Pada artikel Matematika kelas 7 kali ini, kamu akan mengetahui cara menyelesaikan operasi perpangkatan bentuk aljabar. Yuk, kita pelajari selengkapnya!

—

Jika pada artikel sebelumnya kamu telah mengetahui tentang bentuk aljabar dan cara menyelesaikan beberapa operasi hitung aljabar, maka pada artikel kali ini, kita akan lanjut membahas operasi hitung aljabar yang lainnya, yaitu operasi perpangkatan. Tapi sebelum itu, ayo kita mengingat kembali apa itu aljabar, ya. 

Hayo, siapa di antara kamu yang masih ingat apa itu aljabar?

Aljabar adalah salah satu dari cabang Matematika yang mempelajari tentang penyelesaian masalah menggunakan huruf-huruf untuk mewakili angka-angka.

Bentuk aljabar terdiri dari variabel (nilai berubah), konstanta (nilai tetap), dan koefisien (faktor pengali). Misalnya, 2a + 1 nih. Berarti, 2 merupakan koefisiennya, a merupakan variabelnya, dan 1 merupakan konstantanya.

Bagaimana, sampai di sini kamu sudah ingat?

Oke, kalau begitu, selanjutnya mari kita masuk ke operasi perpangkatan pada aljabar, ya. Kira-kira, bagaimana sih cara untuk menyelesaikan operasi perpangkatan pada aljabar? Yuk, langsung saja kita simak pada artikel di bawah ini. Let’s scroll it!

Konsep Perpangkatan Bentuk Aljabar

Sebelumnya, ayo kita simak kisah Rogu berikut ini dan kita selesaikan bersama-sama, ya!

Pada saat upacara bendera di sekolah, Rogu bergabung ke dalam grup paduan suara yang selama ini ia idam-idamkan. Grup tersebut terdiri dari 5 baris.

Baris pertama, bertugas untuk memainkan pianika, baris kedua bertugas untuk memainkan recorder, dan baris ketiga sampai kelima bertugas untuk menyanyikan lagu Indonesia Raya dan Mengheningkan Cipta.

Rogu, berada pada baris pertama yang bertugas untuk memainkan pianika. Setiap baris terdiri dari 5 orang anak. Dapatkah kamu menghitung berapa jumlah seluruh anak yang bergabung dalam grup paduan suara tersebut?

Baca Juga: Pengertian, Jenis, dan Contoh Bilangan Bulat

Nah, untuk menghitung jumlah seluruh anak dalam grup tersebut, kamu dapat menggunakan cara perkalian sebagai berikut:

5 × 5

Ternyata, perkalian di atas termasuk salah satu contoh dari perkalian berulang, lho. Kenapa? Karena perkalian tersebut terdiri dari bilangan dengan faktor-faktor yang sama, yaitu 5.

Tahukah kamu, setiap perkalian berulang dapat ditulis secara ringkas dengan menggunakan notasi bilangan berpangkat seperti di bawah ini:

5² (dibaca 5 pangkat 2)

Jadi jawabannya sudah pada tahu ya, yaitu 5² = 5 × 5 = 25 orang anak.

Oke, agar kamu lebih paham lagi tentang notasi bilangan berpangkat, yuk perhatikan contoh berikut:

2 × 2 × 2 = 2³   (dibaca 2 pangkat 3)

3 × 3 × 3 × 3 = 3⁴   (dibaca 3 pangkat 4)

a × a × a × … × a = aⁿ   (dibaca a pangkat n)

Jika kamu melihat contoh-contoh di atas, maka dapat kamu ketahui kalau perpangkatan adalah suatu bilangan yang dikalikan dengan dirinya sendiri sebanyak jumlah pangkatnya (n kali).

Pada prinsipnya, ternyata rumus perpangkatan pada bentuk aljabar sama dengan perpangkatan pada bilangan bulat.

Rumus Perpangkatan pada Bentuk Aljabar

Bentuk Istimewa dalam Perpangkatan Bentuk Aljabar

Selain itu, terdapat beberapa bentuk istimewa yang akan sering kamu temui dalam perpangkatan aljabar, yaitu:

Contoh Soal Perpangkatan Bentuk Aljabar

Sekarang, yuk, coba kerjakan soal di bawah ini supaya kamu semakin paham!

Contoh 1: 

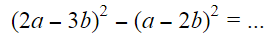
Penyelesaian:

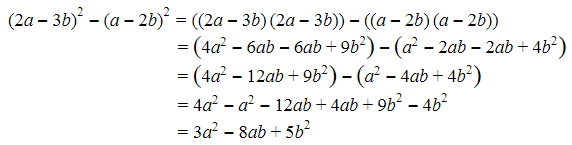
Baca Juga: Mengenal Operasi Hitung pada Pecahan

Contoh 2:

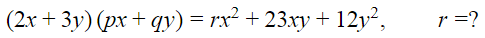
Penyelesaian:

Nah, untuk contoh yang satu ini, penyelesaiannya cukup rumit nih. Jadi, simak baik-baik ya langkah-langkahnya. Oke, langkah pertama yang bisa kamu lakukan untuk menyelesaikan soal di atas adalah operasikan persamaan tersebut seperti biasa.

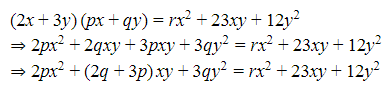
Kemudian, langkah keduanya adalah kita samakan variabelnya.

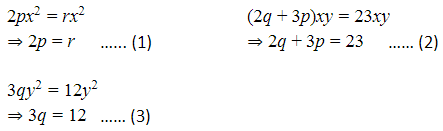
Berdasarkan persamaan (3), didapat nilai q = 4. Lalu, kita substitusikan nilai q ke persamaan (2) menjadi sebagai berikut:

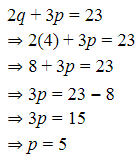
Setelah kita substitusikan niai q ke persamaan (2), didapat nilai p = 5. Selanjutnya, kita substitusikan nilai p ke persamaan (1) menjadi sebagai berikut:

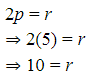
Sehingga, diperoleh nilai r adalah 10.

Bagaimana sampai di sini? Paham atau paham? Bagi kamu yang masih kurang paham, jangan ragu untuk tuliskan pertanyaanmu di kolom komentar, ya.

Berdasarkan penjabaran di atas, sekarang kamu sudah tahu bagaimana cara menyelesaikan operasi perpangkatan pada bentuk aljabar berpangkat dua, kan.

Lalu, bagaimana cara untuk menyelesaikan operasi perpangkatan pada bentuk aljabar yang pangkatnya lebih dari dua? Jawabannya ada dua cara, nih. Penasaran bagaimana caranya? Kalau begitu, yuk langsung simak contohnya di bawah ini!

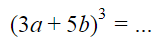
Penyelesaian:

• Cara 1: Menggunakan pola segitiga pascal

Sebelumnya, ayo kita perhatikan ilustrasi gambar pola segitiga pascal berikut ini dulu, ya!

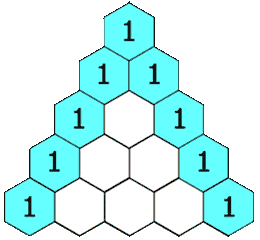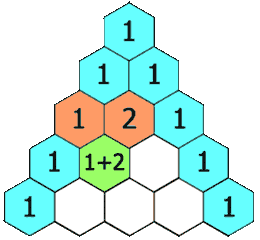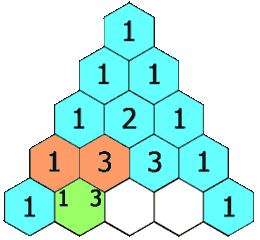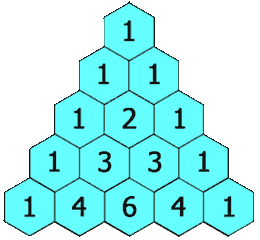
Segitiga pascal (sumber:en.wikipedia.org)

Pada gambar di atas dapat kamu ketahui bahwa, pola bilangan tersebut membentuk bangun segitiga yang selalu diawali dan diakhiri dengan angka 1.

Kemudian, bilangan-bilangan yang selain angka 1 itu diperoleh dari jumlah dua buah bilangan yang terletak di atasnya dan saling berdekatan.

Pola segitiga pascal ini ternyata berhubungan dengan koefisien pada bentuk aljabar, lho. Coba kamu perhatikan gambar di bawah ini!

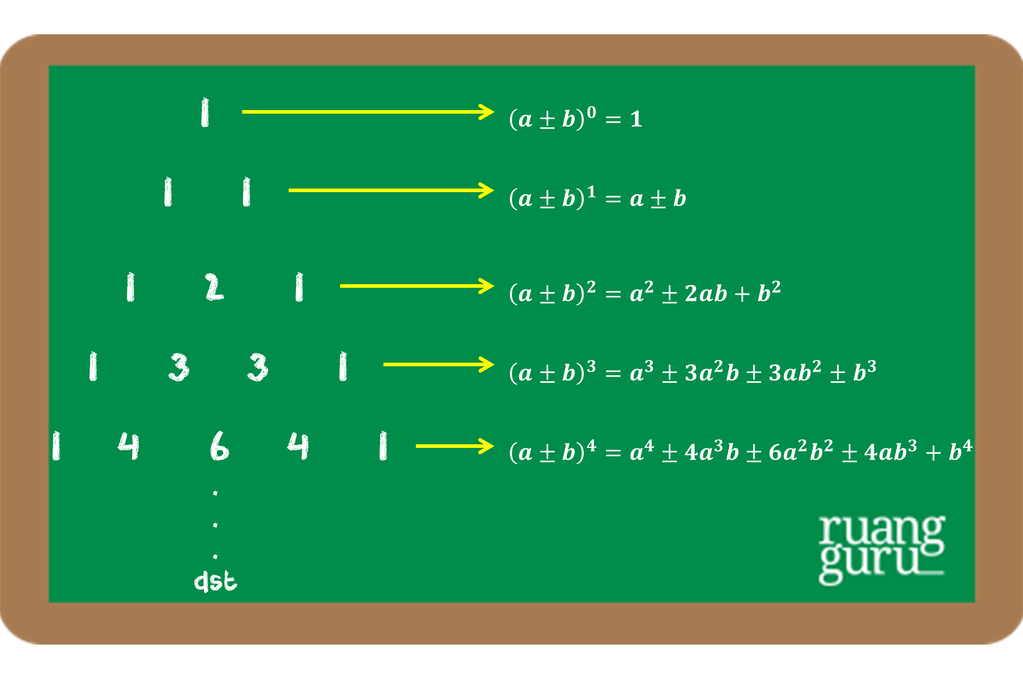
Ternyata, koefisien pada bentuk aljabar di atas sama dengan pola segitiga pascal. Selanjutnya, coba kamu perhatikan besar pangkat pada masing-masing variabelnya.

Ternyata, semakin ke kanan, besar pangkat variabel a akan semakin kecil (aⁿ –> a^n-1 –> … –> a⁰) dan besar pangkat variabel b akan semakin besar (b⁰ –> … –> bⁿ).

Jadi, berdasarkan soal di atas dapat kita peroleh hasil sebagai berikut:

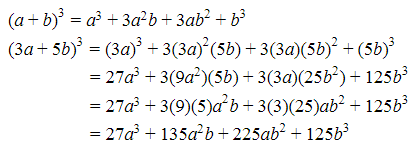
Paham ya dengan cara segitiga pascal ini. Oke, kalau begitu kita lanjut ke cara yang kedua, ya. 

Baca Juga: Jenis-Jenis Bilangan Pecahan dan Contohnya

• Cara 2:

Nah, bagi kamu yang malas menghafal pola segitiga pascal di atas, kamu bisa menggunakan cara yang satu ini. Pada cara ini, kamu hanya tinggal menguraikan aljabar tersebut menjadi sebagai berikut:

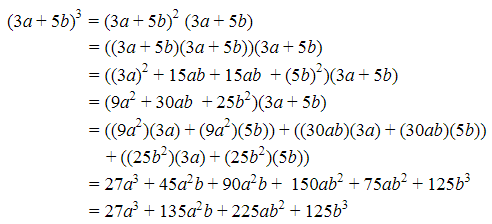
Wah, lumayan panjang ya. Mungkin, untuk menyelesaikan bentuk aljabar dengan pangkat 3 dan 4, cara ini masih cukup efektif. Tapi, bagaimana dengan bentuk aljabar yang pangkatnya 5, 6, 7, dan seterusnya?

Jangan sampai waktu kamu habis hanya untuk menyelesaikan bentuk aljabar yang seperti itu, ya.

Oleh karena itu, ada pentingnya juga nih untuk selalu mengingat pola segitiga pascal yang telah kita pelajari sebelumnya. Selain itu, dalam mengerjakan soal-soal aljabar ini juga dibutuhkan ketelitian yang tinggi.

Perhatikan selalu tanda (+) dan (-) nya karena kedua tanda itu akan berubah ketika kamu melakukan operasi perkalian dan pemangkatan.

—

So, bagaimana tanggapanmu setelah membaca artikel ini? Mudah atau sulit?

Perlu kita akui kalau materi aljabar ini memang cukup rumit, ya. Oleh karena itu, kamu juga perlu untuk memperbanyak latihan soal, nih.

Nah, bagi kamu yang masih belum paham dengan materi ini dan ingin tanya-tanya lebih lanjut lagi, kamu bisa lho gabung dengan Ruangguru Privat. Belajar jadi semakin asik karena kamu bisa berdiskusi dengan kakak-kakak Tutor lulusan PTN terbaik di Indonesia!

Referensi:

Manik D.R, (2009) Penunjang Belajar Matematika untuk SMP/MTs Kelas 7. Jakarta: Pusat Perbukuan, Departemen Pendidikan Nasional.

Sumber foto:

Ilustrasi ‘Segitiga Pascal’ [Daring]. Tautan: https://upload.wikimedia.org/wikipedia/commons/0/0d/PascalTriangleAnimated2.gif (Diakses: 28 Desember 2020)