Mengenal Ilmu Tertua dalam Matematika: Geometri! | Matematika Kelas 12

Artikel ini membahas mengenai geometri bidang datar, meliputi pengertian, objek-objek geometri, serta hubungan antarobjek geometri.
—
Halo! Sebelumnya kamu sudah banyak sekali belajar tentang ilmu-ilmu dasar dalam Matematika. Mulai dari mengenal jenis-jenis bilangan, himpunan, aljabar, hingga trigonometri. Kali ini, kita akan membahas satu lagi ilmu dasar Matematika yang banyak sekali manfaatnya, terutama untuk mendukung ilmu-ilmu lain, seperti Fisika, Kimia, dan lain sebagainya. Tentunya kamu sudah tahu ya apa yang ingin kita bahas. Yaps! Ia adalah Geometri. Ayo cari tahu apa itu geometri lewat artikel ini. Let’s check this out!
Apa Itu Geometri?
Saat mendengar kata geometri, apa yang kamu bayangkan? Segitiga, persegi, lingkaran, tabung, bola, sebuah garis atau sudut, atau bahkan, nggak ada gambaran sama sekali.

Geometri itu apa, sih? (sumber: giphy.com)
Tenang, di sini kita akan pelajari sama-sama, ya. Jadi, geometri adalah ilmu yang mempelajari hubungan antara objek-objek geometri, seperti titik, garis, bangun, dan sudut.
Geometri merupakan cabang ilmu tertua dalam Matematika. Banyak ilmuwan jaman dulu yang telah mempelajari ilmu ini, seperti Thales, Pythagoras, dan Euclid, tiga tokoh yang berpengaruh dalam ilmu geometri dan karyanya telah banyak dikembangkan oleh ilmuwan lainnya.

Geometri juga memiliki cakupan yang sangat luas. Saking luasnya, rasanya tidak akan cukup jika dibahas dalam satu artikel ini. Oleh karena itu, kita akan mulai belajar dari yang sederhana dulu ya, yaitu geometri bidang datar. Tapi, sebelum itu, kita pahami dulu yuk macam-macam objek geometri berikut ini.

Seperti yang sudah dijelaskan sebelumnya, geometri memiliki 4 objek bahasan, yaitu titik, garis, bangun (datar dan ruang), dan sudut. Kamu pasti sudah tahu dong apa itu titik, garis, bangun, serta sudut. Tapi, di sini kita akan kembali membahas keempat objek geometri tersebut secara ringkas.
1. Titik
Titik merupakan bagian terkecil dari objek geometri karena tidak memiliki ukuran tertentu, baik panjang, lebar, maupun tebal. Titik biasanya disimbolkan dengan “ . ” dan diberi nama dengan huruf kapital (A, B, O, …, dsb). Suatu titik akan menunjukkan posisi atau letak tertentu dari suatu objek.
2. Garis
Garis merupakan himpunan atau kumpulan titik-titik yang tidak berujung. Jika garis hanya memiliki pangkal tanpa adanya ujung, maka disebut sinar garis. Tapi, jika garis tersebut memiliki pangkal dan ujung, maka disebut segmen garis.

3. Bangun
Jika beberapa garis saling berhubungan dan memenuhi syarat-syarat tertentu, maka akan terbentuk sebuah bangun. Bangun ini terbagi menjadi dua, bangun datar dan bangun ruang. Kamu pasti sudah tahu ya bedanya bangun datar dengan bangun ruang?
4. Sudut
Sudut merupakan daerah yang terbentuk dari dua sinar garis dengan pangkal yang sama. Suatu sudut diberi nama dengan satu atau tiga huruf kapital (∠A, ∠ABC, dsb). Sudut juga banyak sekali jenisnya, tergantung dari besar sudut tersebut. Nah, alat untuk mengukur besar sudut adalah busur derajat. Satuan sudut adalah derajat (o) atau 𝛑 radian (1𝛑 radian = 180o).
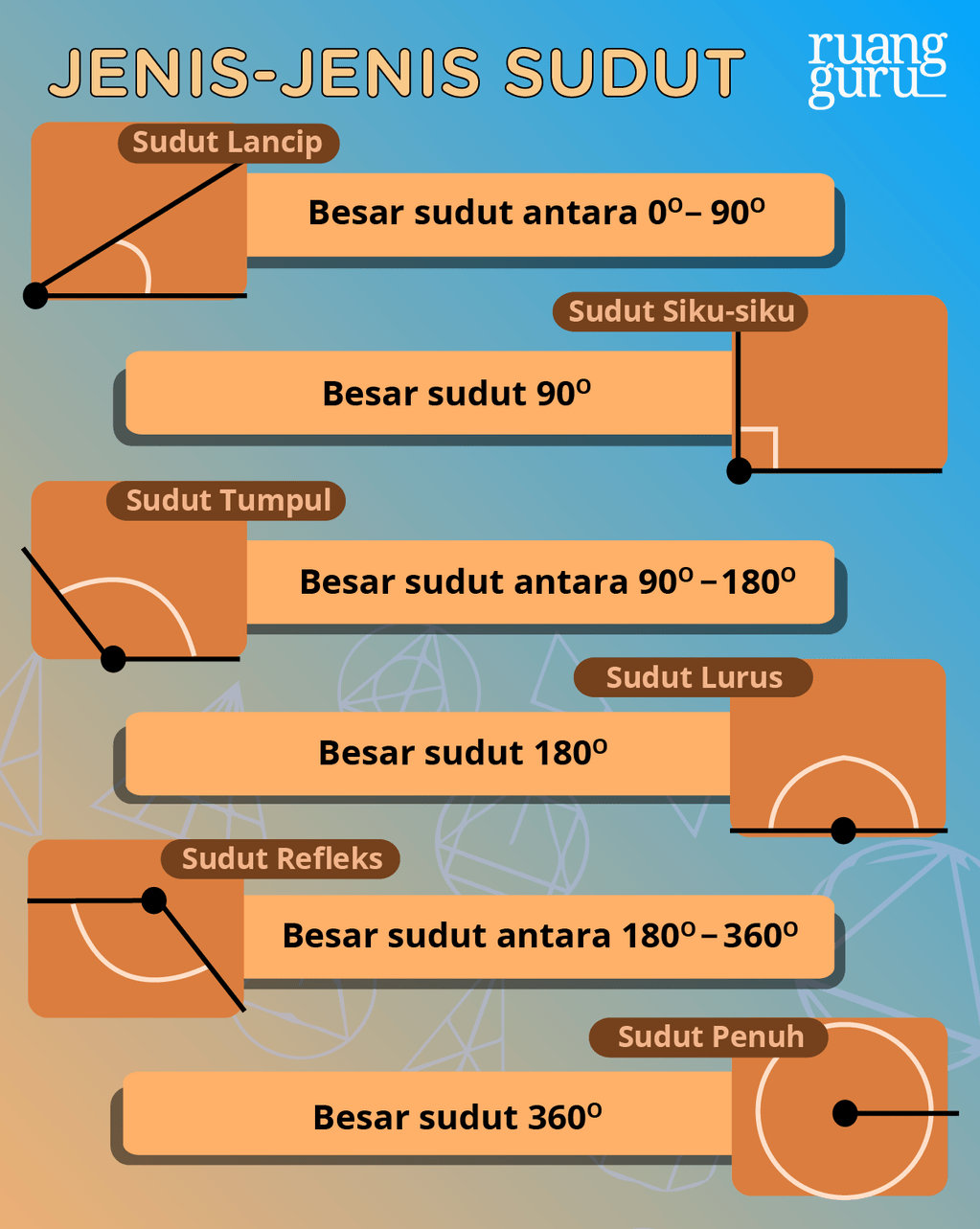
Wah, banyak juga ya ternyata jenis-jenis sudut. Kirain, cuma tumpul, lancip, sama siku-siku aja.
Oke, sebelumnya, sudah dijelaskan kalau di geometri itu, kita akan membahas hubungan antara objek-objek geometri. Nah, materi berikutnya, kita akan mengetahui hubungan antara titik dan garis pada suatu bidang. Hubungannya bagaimana? Hubungan yang dimaksud ini terkait dengan posisi atau kedudukan dari kedua objek geometri tersebut. Supaya lebih jelas, langsung aja yuk kita baca uraian berikut ini.

Terdapat macam-macam kedudukan titik dan garis pada suatu bidang datar, antara lain:
1. Kedudukan titik pada garis
Misalkan, terdapat garis AB dan dua buah titik X dan Y. Maka,
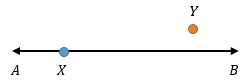
Titik X terletak pada garis AB dan titik Y terletak di luar garis AB.
2. Kedudukan titik pada bidang
Misalkan, terdapat sebuah bidang datar B dan tiga buah titik X, Y, dan Z. Maka,
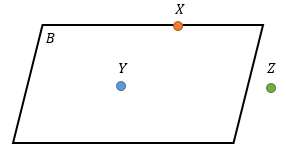
Titik X terletak pada bidang B, titik Y terletak di dalam bidang B, dan titik Z terletak di luar bidang B.
3. Kedudukan garis pada bidang
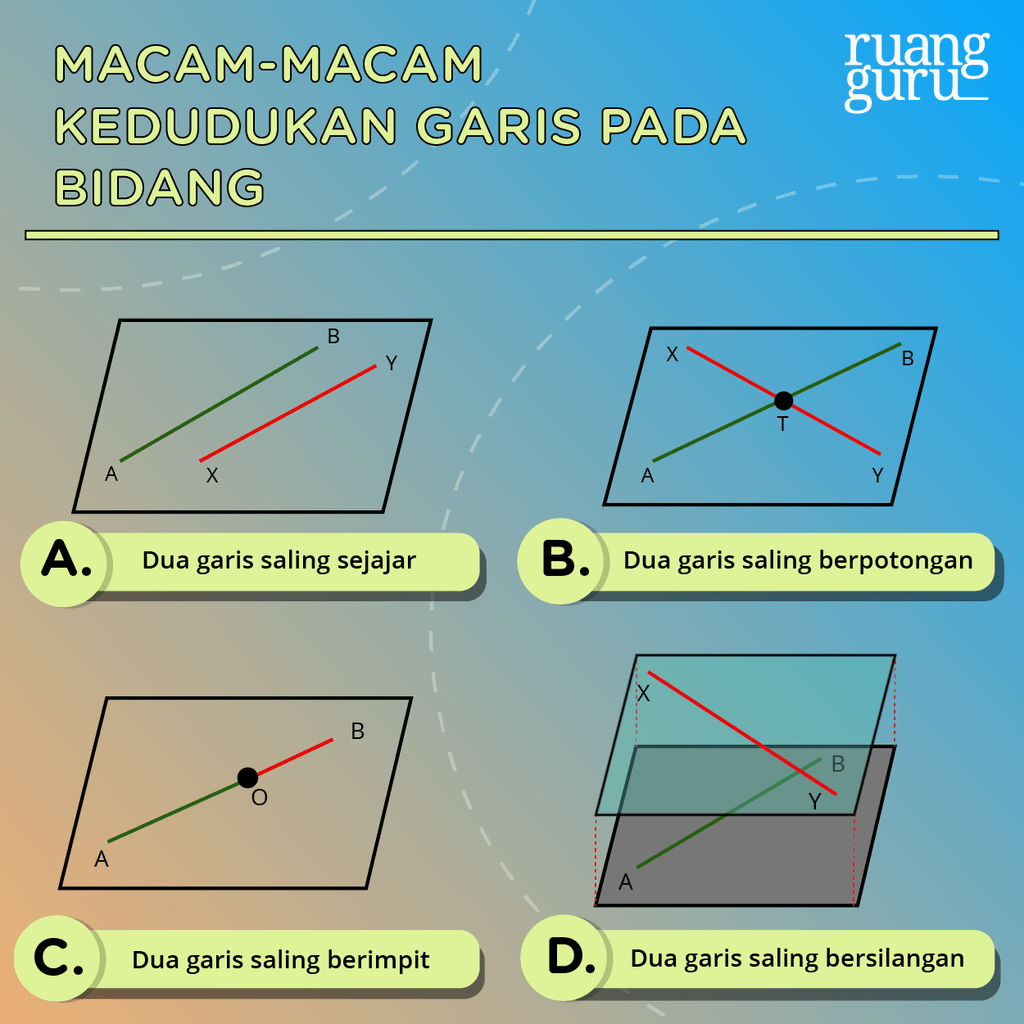
a. Dua garis saling sejajar
Dua garis dikatakan sejajar apabila dua garis tersebut terletak pada bidang yang sama, jarak antar garis selalu tetap, dan tidak memiliki titik persekutuan (tidak berpotongan).
b. Dua garis saling berpotongan
Dua garis dikatakan berpotongan apabila dua garis tersebut terletak pada bidang yang sama dan saling bertemu di satu titik yang dinamakan titik persekutuan.
c. Dua garis saling berimpit
Dua garis dikatakan berimpit apabila dua garis tersebut terletak pada satu garis lurus pada bidang yang sama.
d. Dua garis saling bersilangan
Dua garis dikatakan bersilangan apabila dua garis tersebut tidak terletak pada bidang yang sama dan tidak saling sejajar ataupun berpotongan.
Jelas ya sampai sini? Kalau gitu, kita lanjut ke hubungan objek geometri yang lain, yaitu sudut.

1. Sudut saling berpenyiku (berkomplemen)
Dua sudut dikatakan berpenyiku apabila dua sudut tersebut membentuk sudut siku-siku (90o) dengan salah satu sudutnya merupakan penyiku dari sudut yang lain.
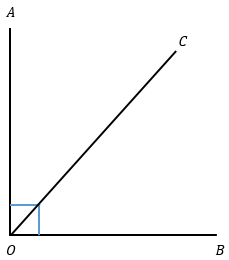
∠BOC penyiku dari ∠AOC atau sebaliknya. ∠BOC + ∠AOC = 90o.
2. Sudut saling berpelurus (bersuplemen)
Dua sudut dikatakan berpelurus apabila dua sudut tersebut membentuk sudut lurus (180o) dengan salah satu sudutnya merupakan pelurus dari sudut yang lain.
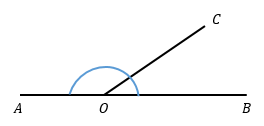
∠BOC pelurus dari ∠AOC atau sebaliknya. ∠BOC + ∠AOC = 180o.
3. Sudut saling bertolak belakang
Dua sudut dikatakan bertolak belakang apabila dua sudut tersebut memiliki arah hadap yang berlawanan. Sudut-sudut yang bertolak belakang memiliki besar sudut yang sama, lho.
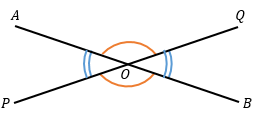
∠BOQ bertolak belakang dengan ∠POA (∠BOQ = ∠POA) dan ∠POB bertolak belakang dengan ∠AOQ (∠POB = ∠AOQ).
4. Hubungan antarsudut pada dua garis sejajar yang dipotong garis lain
Misalkan terdapat dua garis sejajar, yaitu p dan q yang dipotong oleh garis r di titik A dan B. Akibatnya, terbentuk sudut-sudut dengan berbagai sifat tertentu, yaitu:
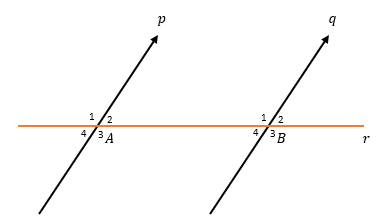
a. Sudut sehadap
Sudut yang menghadap arah yang sama. Contohnya, ∠A1 dan ∠B1, ∠A2 dan ∠B2, ∠A3 dan ∠B3, ∠A4 dan ∠B4.
b. Sudut dalam berseberangan
Sudut yang letaknya di dalam (antara garis p dan q) dan letaknya berseberangan. Contohnya, ∠A2 dan ∠B4, ∠A3 dan ∠B1.
c. Sudut luar berseberangan
Sudut yang letaknya di luar garis p dan q dan letaknya berseberangan. Contohnya, ∠A1 dan ∠B3, ∠A4 dan ∠B2.
d. Sudut dalam sepihak
Sudut yang letaknya di dalam (antara garis p dan q) dan terletak di sisi yang sama. Contohnya, ∠A2 dan ∠B1, ∠A3 dan ∠B4.
e. Sudut luar sepihak
Sudut yang letaknya di luar (antara garis p dan q) dan terletak di sisi yang sama. Contohnya, ∠A1 dan ∠B2, ∠A4 dan ∠B3.
Fiuhh… banyak juga ya materi yang kita bahas kali ini. Eits! tunggu dulu. Supaya materi yang kamu baca tadi nggak buyar gitu aja, kita coba latihan soal, yuk!
Sebenarnya, materi geometri ini sudah kamu pelajari sejak SMP. Kita hanya mengulas dan merangkumnya kembali. Materinya juga nggak terlalu sulit dan merupakan dasar untuk mempelajari materi geometri yang lebih kompleks. Tapi, biasanya kan yang dasar-dasar gini yang sudah kamu lupa. Iya, nggak? Topik geometri bidang datar juga sering kali keluar di soal-soal UTBK, lho! Contohnya saja seperti soal di atas.
Kamu juga jangan malas untuk mengulas kembali materi-materi dasar dari sekarang ya sebagai persiapan untuk menghadapi ujian masuk perguruan tinggi nanti. Download juga aplikasi ruangbelajar supaya belajar kamu jadi nggak membosankan. Semangat kawan!
Sumber Referensi:
Sharma S. N, Widiastuti N, Himawan C, dkk (2017) Jelajah Matematika SMA Kelas XII Program Wajib. Jakarta: Yudhistira.
Artikel diperbarui 25 Januari 2021
![[AB] Web Side Banner - Blog RG](https://cdn-web-2.ruangguru.com/landing-pages/assets/399009fa-feaf-4b6c-8321-92409d53a26a.png)














