Sejarah, Konsep Rumus Teorema Pythagoras & Contoh Soal | Matematika Kelas 8

Ayo, kita belajar bersama-sama materi tentang rumus Teorema Pythagoras, cara menghitungnya dengan mudah, hingga sejarahnya di artikel Matematika kelas 8 ini!

—

Apakah kamu pernah mendengar Pythagoras? Ia merupakan seorang matematikawan dan filsuf Yunani yang dikenal sebagai “Bapak Bilangan”. Salah satu peninggalannya yang bersejarah, yaitu  Teorema Pythagoras! 

Di artikel kali ini, kita akan belajar sama-sama mengenai Teorema Pythagoras. Apa sih Teorema Pythagoras itu? Dari mana asal-usul rumus Teorema Pythagoras? Seperti apa ya cara menghitungnya? Nah, langsung aja simak pembahasan berikut ini, ya!

Sejarah di Balik Teorema Pythagoras

Layaknya Hukum Newton yang ditemukan oleh Sir Isaac Newton, atau Hukum Archimedes yang ditemukan oleh Archimedes, kebanyakan dari kamu mungkin mengira kalau Teorema Pythagoras juga ditemukan oleh Bapak Bilangan satu ini, deh.

Nyatanya, Pythagoras bukanlah penemu pertama dari teorema ini, loh! Loh, kok? Kenapa bisa ya, bukan orang yang menemukan, tapi namanyalah yang digunakan untuk teorema ini? Mari kita simak sejarahnya, guys!

Sebenarnya, Teorema Pythagoras sudah digunakan sejak lama, yaitu sekitar abad ke 1900 – 1600 SM oleh bangsa Mesir, Babilonia, dan Cina Kuno. Mereka sudah memiliki pemahaman mengenai relasi (hubungan) antara sisi-sisi segitiga siku-siku, jauh sebelum Pythagoras lahir.

Salah satu bukti sejarahnya, yakni penemuan tablet milik peradaban bangsa Babilonia. Pada tablet tersebut, tertulis banyak kombinasi 3 angka yang memenuhi syarat Teorema Pythagoras. Kalau sekarang sih, kita menyebutnya dengan Triple Pythagoras. Diperkirakan bahwa pengetahuan inilah yang mendasari bangsa peradaban kuno untuk membangun piramida.

Namun, Pythagoras juga tidak semena-mena mengklaim mengenai teorema itu, ya. Ia mendapat penghargaan atas teorema ini karena dianggap telah menyebarkan pengetahuan tersebut ke peradaban Yunani, serta telah membuktikan rumusnya secara sistematis. Nah, sejak saat itulah pengetahuan menganai relasi antara sisi-sisi segitiga siku-siku dinamakan Teorema Pythagoras.

Bagaimana Konsep Rumus Teorema Pythagoras Itu?

Teorema Pythagoras adalah teorema yang menjelaskan hubungan panjang sisi pada segitiga siku-siku. Oleh karena itu, teorema ini hanya berlaku pada segitiga siku-siku aja. Kamu tau kan, segitiga siku-siku itu kayak gimana?

Eits, cara mengenali segitiga siku-siku itu gampang, kok. Salah satu cirinya adalah besar sudut sikunya ada yang 90^o. Nah, sekarang, coba deh kamu lihat gambar segitiga siku-siku di bawah ini!

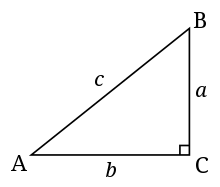Segitiga siku-siku (sumber: id.wikipedia.co.id)

Misalkan ada segitiga siku-siku ABC, seperti pada gambar di atas. Sisi-sisi pada segitiga tersebut dinamai sesuai dengan nama sudut di depannya. Jadi, kalo sisi dari titik A ke B, bisa dinamai dengan c, karena sudut di depan sisi tersebut adalah ∠C . Hal yang harus kamu ingat, penamaan nama sisi itu harus pakai huruf kecil, ya.

Kemudian, sisi a dan b merupakan sisi tegak pada segitiga siku-siku. Kenapa disebut sisi tegak? Soalnya, kedua sisi tersebut membentuk sudut siku-siku (90^o). Sementara itu, sisi c merupakan sisi miring (hipotenusa) segitiga siku-siku. Nah, sisi hipotenusa ini selalu berhadapan dengan sudut siku-sikunya, dan jadi sisi yang paling panjang, guys.

Baca Juga: Jenis-Jenis Bilangan Pecahan dan Contohnya

Bunyi Teorema Pythagoras

Nah, Teorema Pythagoras menyatakan bahwa kuadrat panjang hipotenusa pada suatu segitiga siku-siku (salah satu sudutnya 90°) adalah sama dengan jumlah kuadrat panjang sisi-sisi lainnya. Atau, kalau mau dituliskan secara matematis, akan seperti ini:

Dengan c adalah hipotenusa yang juga merupakan sisi terpanjang dari segitiga siku-siku, sedangkan a dan b adalah sisi-sisi segitiga siku-siku lainnya. Gimana, sampai sini, apakah kamu mulai paham dengan rumus Teorema Pythagoras? Oke, supaya belajarnya lebih mantap lagi, kita coba kerjakan latihan soal di bawah ini, yuk!

Contoh Soal Teorema Pythagoras

Teorema Pythagoras ini bisa digunakan untuk mencari panjang sisi pada segitiga siku-siku yang belum diketahui, lho. Contohnya pada soal berikut!

Contoh Soal 1

1. Terdapat segitiga PQR siku-siku di Q. Jika diketahui panjang sisi PQ = 5cm dan QR = 12 cm, maka panjang sisi PR adalah…

Penyelesaian:

Supaya lebih mudah dalam menghitung, kita gambar dulu segitiga siku-sikunya, seperti ini:

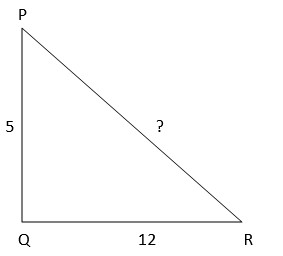
Sehingga,

PQ² + QR² = PR²

5² + 12² = PR²

25 + 144 = PR²

169 = PR²

PR = ±√169

PR = ±13

Nah, karena PR itu panjang hipotenusa, yang artinya tidak boleh negatif, maka nilai PR yang memenuhi adalah 13 cm.

Contoh Soal 2

2. Segitiga siku-siku KLM, jika panjang KL = 2,5 m dan KM = 6,5 m, maka keliling segitiga KLM adalah …

Penyelesaian:

Keliling segitiga KLM bisa dicari dengan menjumlahkan ketiga sisinya. Berarti, kita cari terlebih dulu panjang sisi LM menggunakan Teorema Pythagoras.

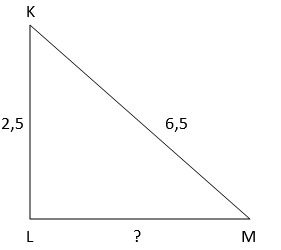
KL² + LM² = KM²

LM² = KM² – KL²

LM² = (6,5)² – (2,5)²

LM² = 42,25 – 6,25

LM² = 36

LM = ±√36

LM = ± 6

Inget ya, kita pilih yang tandanya positif karena panjang sisi nggak mungkin negatif. Jadi, panjang sisi LM adalah 6 m. Sehingga, keliling segitiga KLM adalah,

Keliling segitiga KLM = KL + LM + KM = 2,5 + 6 + 6,5 = 15 m.

Baca Juga: Cara Menyelesaikan Bentuk-Bentuk Aljabar

Hubungan Teorema Pythagoras dengan Jenis Segitiga

Meskipun rumus Teorema Pythagoras hanya bisa digunakan untuk mencari sisi-sisi pada segitiga siku-siku, tapi kita juga bisa menggunakan teorema ini untuk mencari tahu bagaimana bentuk segitiga hanya dari nilai sisi-sisinya saja.

Misalkan, kita punya segitiga dengan a, b, dan c merupakan sisi-sisi segitiga tersebut. Maka sisi a, b, dan c dapat membentuk segitiga dengan tiga kemungkinan, di antaranya:

Jadi, dengan menggunakan Teorema Pythagoras, kita juga dapat menentukan, apakah ketiga barisan bilangan dapat membentuk segitiga siku-siku atau tidak. Contoh:

Diketahui sisi-sisi sebuah segitiga, yaitu a = 10, b = 8 dan c = 22. Dengan mengudaratkan sisi miring dan jumlahkan kuadrat sisi lainnya, maka diperoleh:

c² = 22²

c² = 484

a² + b² = 10² + 8²

a² + b² = 100 + 64

a² + b² = 164

Karena 164 < 484 atau a² + b² < c² (10² + 8² < 22²), maka segitiga ini bukan termasuk segitiga siku-siku, melainkan segitiga tumpul.

Apa Itu Triple Pythagoras?

Setelah memahami isi dari Teorema Pythagoras, kita lanjut ke bahasan berikutnya, nih, yaitu Triple Pythagoras. Waduh, apa lagi, tuh? Triple Pythagoras adalah pasangan tiga bilangan asli yang memenuhi Teorema Pythagoras.

Beberapa pasangan 3 bilangan asli yang memenuhi Triple Pythagoras, di antaranya:

Triple Pythagoras ini bisa membantu kita untuk menentukan, mana kumpulan bilangan yang termasuk segitiga siku-siku dengan cara yang lebih cepat. Oke, supaya kamu nggak bingung, kita masuk ke contoh soalnya aja, ya.

Misalnya, diketahui segitiga dengan panjang sisi-sisinya, yaitu 6, 8, dan 10. Nah, menurutmu, apakah ketiga sisi tersebut merupakan triple Pythagoras?

Jawabannya, iya. Karena 6, 8, dan 10 merupakan kelipatan dari 3, 4, dan 5. Alhasil segitiga tersebut pasti merupakan segitiga siku-siku. Cepat kan ya?

Manfaat Teorema Pythagoras dalam Kehidupan Sehari-hari

Gunanya apa sih belajar Teorema Pythagoras? Tenang, setiap ilmu yang kamu pelajari, pasti ada manfaatnya, kok. Tidak ada yang sia-sia di dunia ini (ciee…).

Di jenjang SMA nanti, materi Teorema Pythagoras masih tetap dipelajari, sebagai dasar untuk mempelajari Trigonometri, yaitu salah satu cabang ilmu Matematika yang membahas hubungan antara panjang dan sudut segitiga. Sementara itu, di kehidupan sehari-hari, Teorema Pythagoras juga punya kegunaan yang cukup penting. Di antaranya:

1. Sistem Navigasi

Dalam sistem navigasi, ada yang namanya metode triangulasi yang digunakan untuk menentukan lokasi atau koordinat berdasarkan sudut antar titik koordinatnya. Nah, Teorema Pythagoras dapat dimanfaatkan ketika triangulasi menggunakan sudut 90.

Sementara itu, para pelaut menggunakan teorema ini untuk menghitung rute terpendek dengan menggambar dua garis vertikal dan dua garis horizontal dari posisi kapal, pilot menggunakan teorema ini untuk menentukan geolokasi yang tepat untuk memulai penurunan yang aman menuju bandara tujuan, dan kita bisa menggunakan Teorema Pythagoras untuk sistem navigasi mobil atau pelacakan ponsel.

2. Arsitektur dan Konstruksi

Dalam bidang arsitektur dan konstruksi, Teorema Pythagoras bisa diaplikasikan, khususnya pada bangunan atau bidang yang berbentuk segitiga. Contohnya, atap bangunan. Rumus dasar teorema Pythagoras, yang menyatakan bahwa sebuah segitiga akan selalu memiliki sudut tegak jika sisi-sisinya memenuhi kondisi tertentu, digunakan oleh para insinyur dalam membuat kerangka bangunan ini.

3. Desain Layar Televisi atau Monitor

Kamu tahu nggak, ukuran TV dan monitor selalu ditentukan dalam satuan diagonal, loh. Misalnya, jika sebuah televisi memiliki ukuran 32 inci, maka ukuran keseluruhannya dilakukan menggunakan pengukuran diagonal, yang dikenal sebagai sisi miring (hipotenusa). Jadi, dengan kata lain, Teorema Pythagoras juga bermanfaat dalam membantu mengukur layar TV, monitor, atau bahkan layar HP kamu.

Nah, selain manfaat di atas, Teorema Pythagoras juga merupakan dasar untuk banyak bidang di luar matematika, mulai dari fisika, geologi, arsitektur, dan lainnya.

Baca Juga: Pengertian dan Cara Menghitung Bruto, Netto, dan Tara

Ternyata, mudah ya cara menentukan panjang sisi-sisi pada segitiga siku-siku dengan menggunakan Teorema Pythagoras itu. Kalau kamu punya cara lain yang diajarkan sekolahmu, boleh juga di-share di kolom komentar supaya yang lain tahu! Tentunya, kamu dapat memelajari materi seperti ini dengan cara yang lebih asyik. Seperti menonton video beranimasi dari ruangbelajar, misalnya. Di sana, kamu akan mendapatkan rangkuman dan latihan-latihan soal yang membantumu memahami lebih dalam tentang pelajaran sekolah, lho!

Referensi:

Raharjo M, Setiawan A. (2018) Matematika SMP/MTs Kelas VIII. Jakarta: Erlangga

Sumber foto:

Ilustrasi ‘Segitiga Siku-Siku’ [Daring]. Tautan: https://id.wikipedia.org/wiki/Segitiga_siku-siku (Diakses: 21 Januari 2022)

Artikel diperbarui pada 3 Januari 2024.