Mempelajari Barisan dan Deret Geometri | Matematika Kelas 11

Yuk, kita mempelajari barisan geometri, deret geometri, dan deret geometri tak hingga! Seperti apa bentuknya dan bagaimana rumus-rumusnya? Simak artikel berikut ini, ya!

—

Jika kamu sudah membaca artikel tentang barisan dan deret aritmatika, kamu pastinya sudah tahu manfaat dari mempelajari konsep barisan dan deret dalam matematika. Nah, selain barisan dan deret aritmatika, ada satu lagi nih, yang mau kita bahas di artikel ini, yaitu barisan dan deret geometri.

Apa itu barisan dan deret geometri? Apa sih, perbedaannya dengan barisan dan deret aritmatika? Oke, supaya kamu nggak bingung, yuk langsung baca penjelasannya di bawah ini!

Barisan geometri adalah pola yang memiliki pengali atau rasio yang tetap untuk setiap 2 suku yang berdekatan. Rasio pada barisan geometri biasa disimbolkan dengan r. Barisan geometri juga biasa disebut sebagai barisan ukur.

Contoh lebih mudahnya begini, misal kamu punya barisan seperti ini:

1, 3, 9, 27, …

Dari barisan tersebut, kita bisa lihat antara suku pertama dengan suku kedua, antara suku kedua dan suku ketiga dan seterusnya selalu punya pengali yang tetap, yaitu 3. Dengan demikian, barisan ini termasuk barisan geometri.

Nah, kalau barisan ini dituliskan dalam bentuk penjumlahan, namanya jadi deret geometri. Deret geometri itu bentuk penjumlahan dari barisan geometri. Penulisannya adalah seperti ini:

1 + 3 + 9 + 27 + …

Paham ya, bedanya barisan dan deret? Lalu, kalau deret geometri tak hingga itu apa?

Deret geometri tak hingga hampir sama dengan deret geometri, namun deret tersebut diteruskan hingga nilainya tak hingga. Nanti kita bahas lebih lanjut ya, supaya kamu bisa lebih paham. Sekarang, kita bahas mulai dari barisan dan deret geometri dulu, yuk! Lalu selanjutnya kita akan bahas tentang deret geometri tak hingga.

Barisan Geometri dan Deret Geometri

Tadi, kita sudah mengenal pengertian serta contoh dari barisan geometri dan deret geometri. Sekarang, kita belajar rumus-rumusnya, ya!

Pada barisan geometri dan deret geometri, terdapat tiga rumus yang harus kamu ketahui, yaitu rumus rasio, rumus U_n, dan rumus S_n. Kita bahas satu per satu, ya!

1. Rumus Rasio pada Barisan dan Deret Geometri

Rasio adalah nilai pengali pada barisan dan deret. Rumus untuk mencari rasio pada barisan geometri dan deret geometri adalah seperti infografis berikut.

Misalnya kita punya barisan geometri:

1, 3, 9, 27, 81, ….

Suku pertama (a) dari barisan geometri tersebut adalah 1. Maka r-nya adalah:

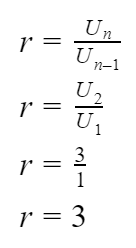
Jadi, rasio dari barisan geometri tersebut adalah 3.

Sekarang kita pelajari rumus suku ke–n (U_n), yuk!

2. Rumus Un pada Barisan dan Deret Geometri

U_n adalah suku ke-n pada barisan dan deret. Untuk mencari U_n pada barisan geometri dan deret geometri, kamu bisa menggunakan rumus berikut ini.

Misalnya kita punya barisan geometri:

1, 3, 9, 27, 81, ….

Lalu, kita coba cari U_n nya. Misalnya n yang mau dicari adalah 6, maka:

U_n = ar^n-1

U₆ = ar⁵

U₆ = 1 . 3⁵

U₆ = 1 . 243

U₆ = 243

Jadi, U₆ dari barisan geometri tersebut adalah 243.

Mudah kan, rumusnya? Syaratnya adalah kamu harus mengetahui berapa nilai a dan r-nya. Dengan begitu, kamu sudah bisa mencari U_n dengan mudah. Sekarang, kita cari tahu rumus selanjutnya yuk!

3. Rumus Sn pada Barisan dan Deret Geometri

S_n adalah jumlah suku ke-n pada barisan dan deret. Nah, bagaimana cara kita mencari tau S_n pada barisan geometri dan deret geometri? Berikut ini adalah rumusnya. Check it out!

Misalnya kita punya barisan geometri:

1, 3, 9, 27, 81, ….

Lalu, kita coba cari S_n nya. Misalnya n yang mau dicari adalah 3, maka:

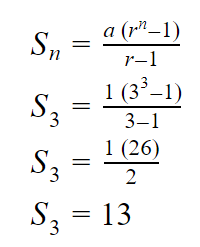
Jadi, S₃ dari barisan geometri tersebut adalah 13.

Oke, itu dia rumus S_n dalam barisan geometri dan deret geometri. Nah sekarang, kita lanjut bahas tentang deret geometri tak hingga, yuk!

Baca juga: Barisan Aritmatika Bertingkat

Deret Geometri Tak Hingga

Deret geometri tak hingga itu dibagi menjadi 2 jenis yaitu deret geometri tak hingga divergen dan deret geometri tak hingga konvergen. Keduanya memiliki perbedaan yang cukup penting. Yuk, kita lihat pengertian dari kedua jenis deret geometri tak hingga tersebut beserta perbedaannya!

1. Deret Geometri Tak Hingga Divergen

Deret geometri tak hingga divergen adalah suatu deret yang nilai bilangannya semakin membesar dan tidak bisa dihitung jumlahnya. Bisa kita lihat seperti di bawah ini,

1 + 3 + 9 + 27 + 81 + ……………

Kalau ditanya berapa sih, jumlah seluruhnya? Jumlah seluruhnya tidak bisa dihitung karena nilainya semakin besar.

2. Deret Geometri Tak Hingga Konvergen

Berbeda dengan deret geometri tak hingga divergen, deret geometri tak hingga konvergen merupakan suatu deret di mana nilai bilangannya semakin mengecil dan dapat dihitung jumlahnya. Seperti di bawah ini:

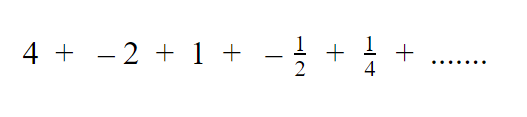
Semakin lama nilainya semakin mengecil dan ujungnya akan mendekati angka 0. Hal ini membuat deret geometri tak hingga konvergen dapat dihitung jika ditanyakan jumlah seluruhnya.

Lalu bagaimana cara menghitung jumlah seluruhnya dari deret geometri tak hingga konvergen?

3. Rumus Stak hingga pada Deret Geometri Tak Hingga Konvergen

Sebelum masuk ke rumus, ada syarat terlebih dahulu jika kamu bertemu dengan deret geometri tak hingga konvergen, yaitu rasionya harus bernilai antara -1 sampai 1 (-1 > r > 1) dan ini berlaku untuk negatif dan positif. Contohnya seperti deret di atas. Deret di atas rasionya adalah 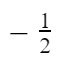 sehingga bisa dihitung jumlah tak hingganya.

Nah, sekarang kita lihat yuk rumus untuk menghitung S_{tak hingga} atau jumlah tak hingganya!

Misalnya kita punya deret geometri tak hingga konvergen:

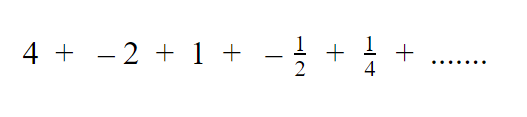
Lalu, kita coba cari S_{tak hingga} nya, maka:

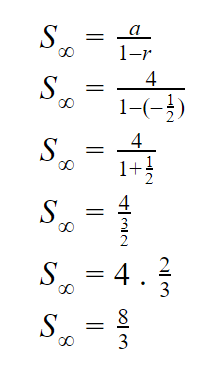
Jadi, S_{tak hingga} darideret geometri tak hingga konvergen tersebut adalah .

Itu dia penjelasan tentang barisan geometri, deret geometri, serta deret geometri tak hingga. Bagaimana, teman-teman? Kamu sudah paham, kan? Atau kamu masih belum puas dengan penjelasannya? Hmm tenang, kamu bisa nih, belajar melalui video animasi di ruangbelajar. Di sana, kamu bisa belajar sekaligus latihan soal-soal. Selain itu, waktu belajar kamu akan lebih efektif, dan tidak akan menyita waktu bermain kamu. Jadiii tunggu apa lagi? Buruan downloadaplikasi ruangguru!

Referensi: