Relasi dan Fungsi: Pengertian, Syarat & Cara Menyatakannya | Matematika Kelas 8

Apa itu relasi dan fungsi? Yuk, kita pelajari mulai dari pengertian, syarat relasi dikatakan fungsi, cara menyatakan relasi dan fungsi, hingga contoh soalnya supaya kamu semakin paham!

—

Dalam belajar Matematika, kamu pasti sudah nggak asing dengan kata relasi dan fungsi bukan? Yup, relasi dan fungsi adalah salah satu konsep yang penting loh untuk memahami materi Matematika lainnya pada tingkatan lanjut.

Selain itu, ada banyak permasalahan Matematika yang dapat diselesaikan menggunakan relasi dan fungsi. Wah, apa itu yaaa? Oke, sebelum kita bahas contoh penerapan materi relasi dan fungsi dalam kehidupan kita seharu-hari, kita pahami dulu yuk pengertian relasi dan fungsi, serta cara menyatakannya di artikel Matematika kelas 8 berikut ini!

Apa itu Relasi?

Nah, pertama-tama, kita pahami dulu apa yang dimaksud dengan relasi. Sepintas sih, relasi itu dimaknai dengan suatu hubungan, entah itu orang, benda, konsep, maupun situasi. Sama halnya dengan istilah relasi dalam Matematika.

Relasi adalah hubungan antara suatu anggota himpunan dengan anggota himpunan lainnya. Himpunan A dan himpunan B dikatakan memiliki relasi jika ada anggota himpunan yang saling berpasangan.

Cara Menyatakan Relasi

Lalu, gimana cara menyatakan relasi? Relasi antara dua himpunan dapat dinyatakan dengan tiga cara, yaitu dengan diagram panah, himpunan pasangan berurutan, dan diagram Cartesius. Yuk, kita bahas satu per satu!

Baca Juga: Sistem Koordinat Kartesius dan Cara Membuat Grafiknya

1. Diagram Panah

Diagram panah merupakan cara yang paling mudah untuk menyatakan suatu relasi. Diagram ini membentuk pola dari suatu relasi ke dalam bentuk gambar arah panah yang menyatakan hubungan antara anggota himpunan A dengan anggota himpunan B.

Misalnya, ada 4 orang anak yaitu Ali, Siti, Amir dan Rizki. Mereka diminta untuk menyebutkan warna favorit mereka. Ali menyukai warna merah, Siti menyukai warna ungu, Amir menyukai warna hitam, dan Rizki menyukai warna merah. Dari hasil uraian tersebut, terdapat dua buah himpunan.

Himpunan pertama adalah himpunan anak, kita sebut himpunan A dan himpunan yang kedua adalah himpunan warna, kita sebut himpunan B. Hubungan antara himpunan A dan himpunan B dapat di ilustrasikan dengan diagram panah seperti berikut:

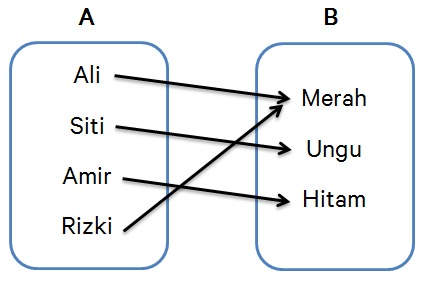
Jadi, dapat disimpulkan bahwa diagram panah di atas merupakan relasi antara anak dengan warna yang mereka sukai. Relasi antara kedua himpunan tersebut dapat dinyatakan dengan panah-panah yang memasangkan anggota himpunan A dengan anggota himpunan B.

2. Himpunan Pasangan Berurutan

Selain dengan diagram panah, suatu relasi juga dapat dinyatakan dengan menggunakan himpunan pasangan berurutan. Caranya dengan memasangkan himpunan A dengan himpunan B secara berurutan. Kita dapat mengambil contoh dari contoh diagram panah tadi.

• Ali menyukai warna merah.
• Siti menyukai warna ungu.
• Amir menyukai warna hitam.
• Rizki menyukai warna merah.

Dari uraian di atas kita dapat menyatakan relasinya dengan himpunan pasangan berurutan seperti berikut:

(Ali, merah), (Siti, ungu), (Amir, hitam), (Rizki, merah)

Jadi, relasi antara himpunan A dengan himpunan B dinyatakan sebagai himpunan pasangan berurutan (x,y) dengan x ∈ A dan y ∈ B.

3. Diagram Cartesius

Kalo cara ini, kita bisa menyatakan relasi antara dua himpunan dari pasangan berurutan yang kemudian dituliskan dalam bentuk dot (titik-titik).

Contoh dari relasi antara anak dengan warna kesukaannya yaitu himpunan A = {Ali, Siti, Amir, Rizki} dan himpunan B = {merah, ungu, hitam}, dapat digambarkan dalam bentuk diagram Cartesius seperti di bawah ini:

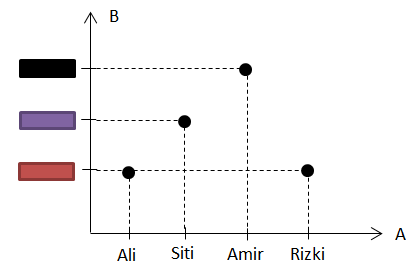
Baca Juga: Bedanya Rumus Barisan & Deret Aritmatika disertai Contoh Soal

Apa itu Fungsi?

Oke, setelah kamu memahami apa itu relasi, kita lanjut ke pengertian fungsi, ya. Fungsi (pemetaan) adalah relasi dari himpunan A ke himpunan B, jika setiap anggota himpunan A berpasangan tepat satu dengan anggota himpunan B.

Semua anggota himpunan A atau daerah asal disebut domain, sedangkan semua anggota himpunan B atau daerah kawan disebut kodomain. Hasil dari pemetaan antara domain dan kodomain disebut range fungsi atau daerah hasil.

Cara Menyatakan Fungsi

Sama halnya dengan relasi, fungsi juga dapat dinyatakan dalam tiga cara, yaitu diagram panah, himpunan pasangan berurutan, dan dengan diagram Cartesius.

Kita ambil satu contoh cara menyatakan fungsi menggunakan diagram panah, ya!

Misalkan, himpunan A = {1,2,3} dan himpunan B = {1,2,3,4}. Fungsi A → B digambarkan sebagai berikut:

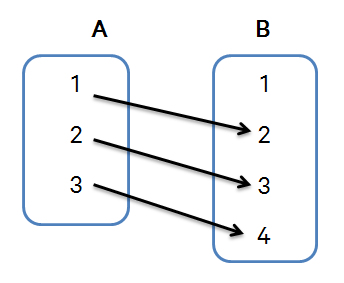
Maka, dari diagram panah di atas dapat disimpukan:

Domain adalah A = {1,2,3}

Kodomain adalah B = {1,2,3,4}

Range fungsi = {2,3,4}

Sampai sini, bisa dikatakan kalo fungsi merupakan bentuk relasi khusus. Setiap fungsi, sudah pasti relasi. Namun, setiap relasi belum tentu merupakan fungsi. Oleh karena itu, ada syarat khusus yang harus dipenuhi relasi agar bisa dikatakan fungsi. Apa saja, ya?

Syarat Relasi dapat Dikatakan Fungsi

Ada dua syarat suatu relasi dapat dikatakan fungsi, yakni:

• Tidak boleh ada anggota domain yang tidak berpasangan. Artinya, seluruh anggota domain harus memiliki pasangan.
• Tidak boleh ada anggota domain yang berpasangan lebih dari satu atau bercabang.

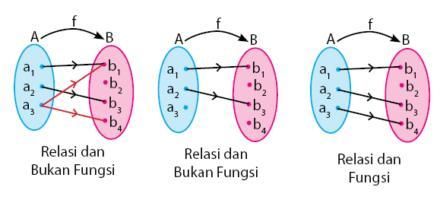
Contoh relasi yang juga merupakan fungsi. (Sumber: Kompas.com)

Nah, kalo kamu perhatikan tiga gambar di atas, ketiganya merupakan relasi, tapi hanya satu yang merupakan fungsi. Kenapa?

Oke, kita lihat gambar paling kiri dulu, ya. Gambar kiri nggak memenuhi syarat fungsi, karena ada satu anggota domain yang berpasangan lebih dari satu, yaitu a3 yang berpasangan dengan b1 dan b4. Jadi, gambar kiri bukan termasuk fungsi.

Lanjut, kita bergeser ke gambar tengah. Kebalikan dengan gambar kiri nih, dimana ada satu anggotanya yang nggak setia (fufufu), kalo gambar tengah, ada satu anggotanya yang jomblo alias nggak punya pasangan :((((  Jadi, gambar tengah juga bukan termasuk fungsi.

Kalo relasi pada gambar kanan dikatakan fungsi, karena setiap anggota domainnya berpasangan satu-satu. Jadi, nggak ada yang punya pasangan dobel, apalagi jones (jomblo ngenes). hehehe…

Paham ya guys, sampai sini?

Baca Juga: Cara Menentukan Persamaan Garis Lurus dan Contohnya

Jenis-Jenis Fungsi

Ada tiga jenis fungsi yang perlu kamu pahami, di antaranya fungsi injektif, surjektif, dan bijektif. Apa tuh ya bedanya?

a. Fungsi Injektif

Fungsi injektif adalah fungsi yang anggota kodomainnya hanya boleh berpasangan dengan satu anggota domain. Pada fungsi injektif, anggota kodomainnya juga boleh tidak memiliki pasangan. Contoh:

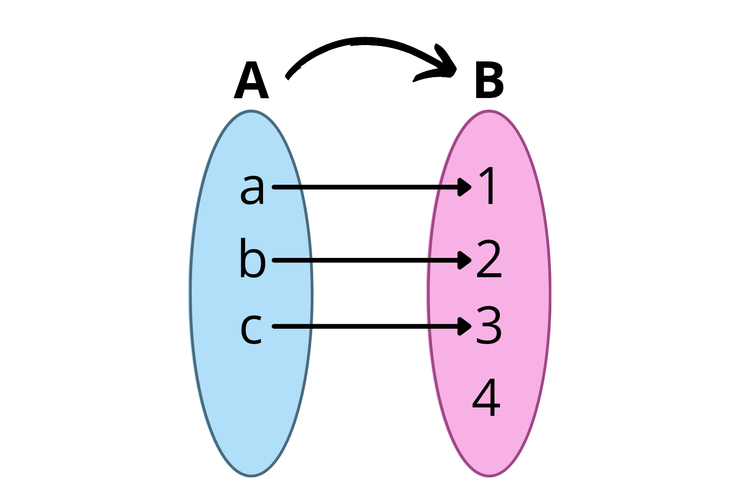
Contoh fungsi injektif. (Sumber: Kompas.com)

Gambar di atas merupakan contoh fungsi injektif karena anggota kodomain (B) berpasangan satu-satu dengan anggota domain (A). Meskipun ada satu anggota kodomain yang tidak berpasangan yaitu 4, fungsi di atas masih bisa dikatakan fungsi injektif, ya.

b. Fungsi Surjektif

Fungsi surjektif adalah fungsi yang anggota kodomainnya tidak boleh ada yang tidak berpasangan. Pada fungsi surjektif, anggota kodomain boleh berpasangan lebih dari satu dengan anggota domain. Contoh:

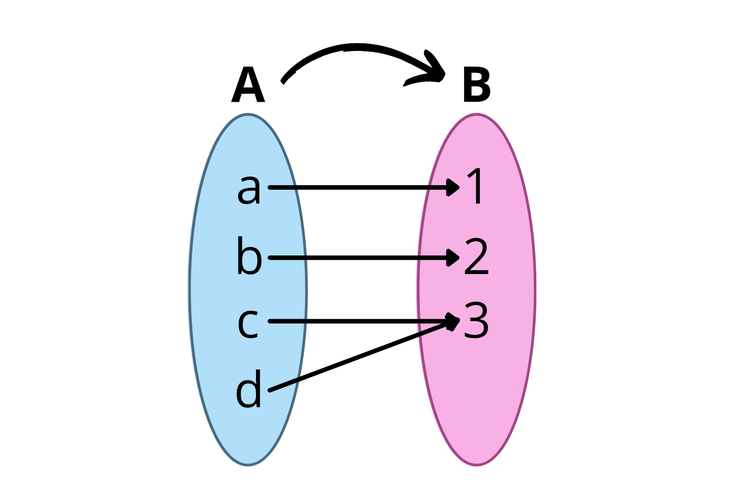
Contoh fungsi surjektif. (Sumber: Kompas.com)

Gambar di atas merupakan fungsi surjektif karena setiap anggota kodomain (B) nggak ada yang jomblo, alias semua punya pasangan dengan anggota domain (A), meskipun ada anggota kodomain yang punya dua pasangan, yaitu (c, 3) dan (d, 3).

c. Fungsi Bijektif

Fungsi bijektif adalah jenis fungsi yang anggota kodomainnya tidak boleh ada yang tidak berpasangan, dan setiap anggota kodomain harus berpasangan dengan tepat satu anggota domain. Contoh:

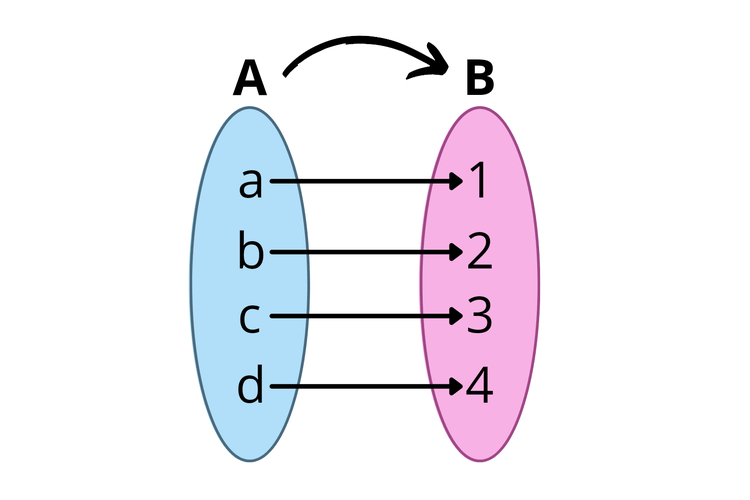
Contoh fungsi bijektif. (Sumber: Kompas.com)

Kalo kita perhatikan gambar fungsi bijektif di atas, semua anggota kodomain (B) punya pasangan satu-satu dengan anggota domain (A). Pada fungsi bijektif ini, jumlah anggota domain harus sama dengan anggota B, sehingga dapat berpasangan satu-satu.

Oh iya, fungsi bijektif juga merupakan fungsi yang memiliki invers, loh! Apa lagi tuh invers? Buat kamu yang penasaran, bisa baca-baca di artikel di bawah ini, ya.

Baca Juga: Apa Itu Fungsi Invers? Pahami Konsep, Rumus & Soalnya, Yuk!

Gais, sejauh ini kamu sudah paham belum dengan konsep relasi dan fungsi? Semoga sudah yaaa. Karena selanjutnya, kita bakal bahas materi fungsi yang lebih kompleks, yaitu notasi fungsi. Let’s go~~~

Notasi Fungsi

Sebuah fungsi dapat dinotasikan dengan huruf kecil, seperti f, g, h, dan lain sebagainya.

Misalnya, fungsi f memetakan himpunan A ke himpunan B, dinotasikan f(x) dengan aturan f : x → 3x + 3.

Artinya, fungsi f memetakan x ke 3x + 3. Jadi, daerah bayangan x oleh fungsi f adalah 3x + 3, sehingga dapat dinotasikan dengan f(x) = 3x + 3. Dari uraian ini dapat dirumuskan:

Jika fungsi f : x → ax + b dengan x anggota domain f , maka rumus fungsif adalah f(x) = ax + b.

Dengan menghitung nilai fungsi, kita dapat mengetahui nilai fungsi yang dapat menghasilkan himpunan kawan (kodomain) dari himpunan asal (domain).

Tenang gais, tenang! Tarik napas, buang napas, minum air segalon. (Sumber: Pinterest.com)

Contoh Soal Fungsi

Oke, oke, supaya lebih jelas, coba kerjakan contoh soal di bawah ini, ya!

Diketahui fungsi f : x → 3x + 3 pada himpunan bilangan bulat. Tentukan:

1. f(3)
2. bayangan (-2) oleh f
3. nilai f untuk x = -4
4. nilai x untuk f(x) = 6
5. nilai a jika f(a) = 12

Pembahasan:

Fungsi f : x → 3x + 3

Rumus fungsi: f(x) = 3x + 3

1. f(3)

Untuk soal nomer satu ini sih gampil, gais. Kamu tinggal mensubstitusi nilai x = 3 ke dalam fungsi. Sehingga,

f(x) = 3x + 3

f(3) → x = 3

f(3) = 3(3) + 3 = 12

Jadi, didapat nilai f(3) = 12.

2. bayangan (-2) oleh f

Etts, jangan panik dulu dengan soalnya. Bayangan (-2) oleh f itu sama dengan f(-2). Jadi,

f(x) = 3x + 3

f(-2) → x = -2

f(-2) = 3(-2) + 3 = -3

Jadi, didapat nilai f(-2) = -3.

3. nilai f untuk x = -4

Soal nomer 3 juga sama konsepnya dengan 2 soal sebelumnya. Sehingga, nilai f untuk x = -4 adalah:

f(x) = 3x + 3

f(-4) → x = -4

f(-4) = 3(-4) + 3 = -9

Jadi, didapat nilai f(-4) = -9.

4. nilai x untuk f(x) = 6

Nah, untuk soal nomer 4 ini jangan sampai terkecoh, ya. f(x) = 6 bukan berarti nilai x = 6. Melainkan, kita harus mencari nilai x agar fungsi tersebut menghasilkan nilai 6. Kita bisa menggunakan cara substitusi sebagai berikut:

3x + 3 = 6

3x = 6 – 3

3x = 3

x = 1

Jadi, didapat nilai x = 1 agar f(x) = 6.

5. nilai a jika f(a) = 12

Soal nomer 5 ini langkah pengerjaannya sama dengan soal nomer 4, ya. Kita bisa menggunakan cara substitusi sebagai berikut:

3a + 3 = 12

3a = 12 – 3

3a = 9

a = 3

Jadi, didapat nilai a = 3 agar f(a) = 12.

—

Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear Dua Variabel (SPLDV)

Nah, sekarang kamu jauh lebih paham kan dengan materi relasi dan fungsi? Jangan lupa terus berlatih soal-soal supaya kamu semakin mahir dalam menghitung nilai fungsi.

Kalau kamu punya contoh soal lain dan bingung cara mengerjakannya, langsung saja tanya dan diskusikan langsung yuk dengan kakak-kakak Tutor di Ruangguru Privat. Kamu bisa sharing sekaligus belajar bersama Tutor terbaik, lho. Seru kan? Yuk, cari tahu informasinya dengan klik banner di bawah ini!

Referensi:

As’ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017) Matematika SMP/MTs Kelas VIII Semester 1. Jakarta: Kementerian Pendidikan dan Kebudayaan.

Sumber Gambar:

Meme Pusing NCT. Tautan: https://id.pinterest.com/pin/586734657735687914/ (Diakses pada 17 Januari 2025)

Sifat-Sifat Fungsi. Tautan: https://www.kompas.com/skola/read/2022/01/03/165019369/sifat-sifat-fungsi (Diakses pada 17 Januari 2025)

Artikel ini pertama kali ditulis oleh Karina Dwi Adistiana, kemudia diperbarui oleh Hani Ammariah pada 17 Januari 2025.